Статический расчет на действие постоянных и временных нагрузок

Постоянная нагрузка.

Задаемся соотношениями между моментами инерции нижней части колонны Iн, верхней части колонны Iв, и моментом инерции ригеля Iр.

; .

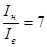
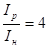
Условно принимаем.

;

;

.

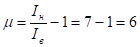
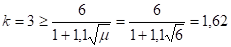
Условие выполняется — ригель абсолютно жесткий.

Сосредоточенный момент из-за смещения осей участков колонн:

.

Каноническое уравнение для левого узла B:

.

Узлам ненагруженной рамы дается смещение на угол .

Коэффициенты для определения реакций:

;

.

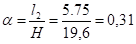
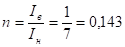
Моменты от поворота узлов стойки на угол (рис. 28, б):

.

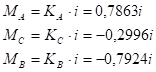
где:

;

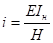
Момент в ригеле:

.

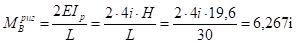
Моменты от нагрузки на стойках (рис. 28, в):

;

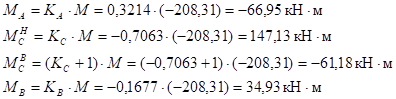
Моменты на опорах ригеля определяются как в защемленной балке:

.

Определяем коэффициенты канонического уравнения:

(по эпюре М1).

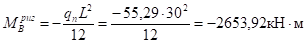
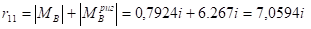
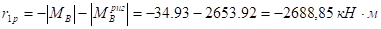
(по эпюре Мр) Угол поворота:

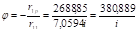
Строим эпюру моментов от постоянной нагрузки (рис. 28, г):

Строим эпюру Q (рис. 28, д):

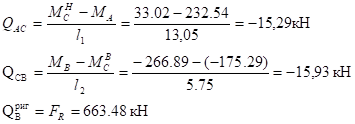
Строим эпюру N (рис. 28, е):

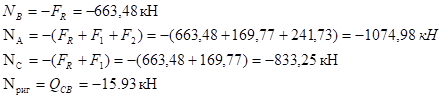
Рис. 27. К расчету рамы на постоянную нагрузку

Снеговая нагрузка.

Находим сосредоточенный момент:

.

Каноническое уравнение:

.

Моменты от нагрузки на стойках:

.

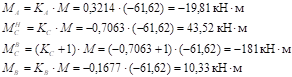
Моменты на опорах ригеля определяются как в защемленной балке:

.

Определяем коэффициенты канонического уравнения:

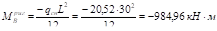
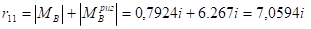
(по эпюре М1);

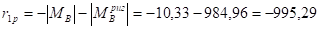
(по эпюре Мp).

Угол поворота:

.

Строим эпюру моментов от постоянной нагрузки:

;

;

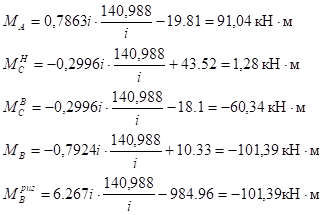
Строим эпюру Q:

;

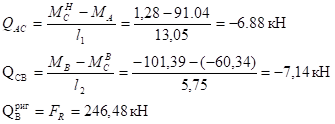
Строим эпюру N:

.

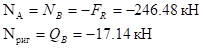
Рис. 28. Эпюры M, Q, N от действия снеговой нагрузки

Вертикальная нагрузка от мостового крана.

Каноническое уравнение для определения смещения рамы:

Моменты и реакции от смещения верхних узлов на =1:

а) для левой стойки.

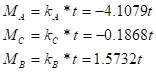
б) для правой стойки.

где kA, kB и kC — коэффициенты для определения изгибающих моментов, определяемые по табл.12.4 [3] в зависимости от значений параметров б и n.

Реакция стойки:

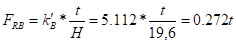
Коэффициенты канонического уравнения:

Моменты и реакции от внешней нагрузки:

а) на левой стойке:

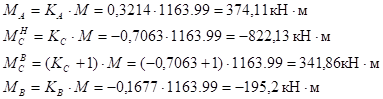
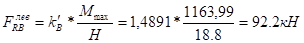
б) на правой стойке:

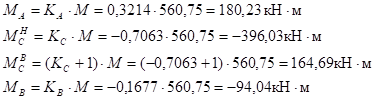
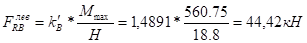
Реакция верхних концов стоек:

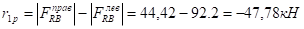
Смещение плоской рамы:

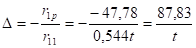
Крановая нагрузка — местная, поэтому бпр? 1. Коэффициент пространственной работы будет равен:

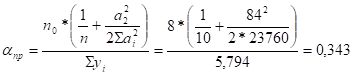
где no — число колес двух кранов на одной нитке подкрановых балок; n — число рам в здании; аi — расстояние между симметрично расположенными относительно середины блока рамами; а2 — расстояние между вторыми от торцов рамами; Yi — сумма ординат линии влияния рассматриваемой рамы.

Смещение с учётом пространственной работы:

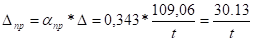
Окончательная эпюра моментов:

М = М1Чпр + МР:

а) левая стойка.

б) правая стойка.

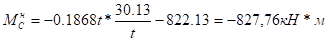
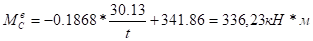
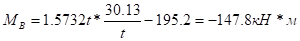
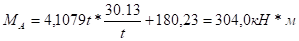
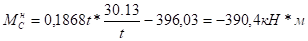
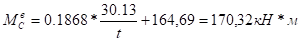
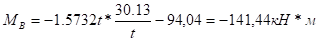
Эпюра поперечных сил:

а) левая стойка.

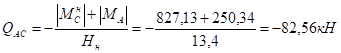
б) правая стойка.

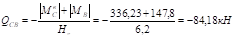
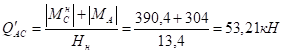
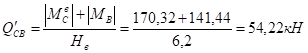
Эпюра продольных сил:

Все правила контроля правильности построения эпюр выполняются.

Рис. 29. Эпюры M, Q, N от действия вертикальной крановой нагрузки

Горизонтальная нагрузка от мостового крана.

Основная система, эпюра М1, каноническое уравнение, коэффициент пр — такие же, как и при расчете на вертикальную нагрузку от мостовых кранов.

Моменты и реакции на левой стойке от нагрузки:

;

;

.

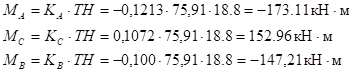
Смещение верхних концов с учетом пространственной работы:

; .

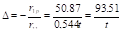
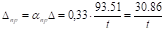
Строим эпюры моментов и поперечных сил от крановой вертикальной нагрузки:

;

— на левой стойке:

;

;

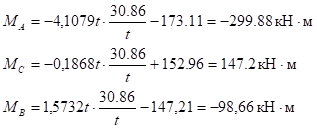
— на правой стойке:

;

.

Строим эпюру N:

.

Все правила контроля правильности построения эпюр выполняются.

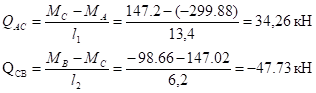
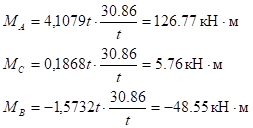
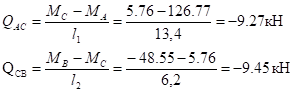
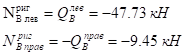
Рис. 31. Эпюры M, Q, N от действия горизонтальной крановой нагрузки.

Ветровая нагрузка.

Основная система и эпюра М1 — как для крановых воздействий.

Моменты и реакции на левой стойке от нагрузки:

;

.

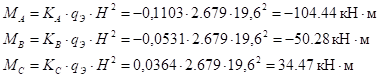
На правой стойке:

.

Коэффициенты канонического уравнения:

;

.

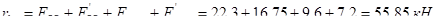
Смещение рамы (ветровая нагрузка воздействует на всю раму, поэтому пр=1):

.

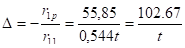
Строим эпюры моментов и поперечных сил от ветровой нагрузки:

;

— на левой стойке:

;

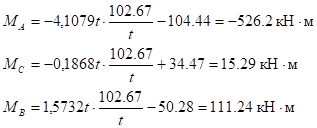
— на правой стойке:

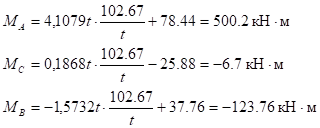
а) левая стойка:

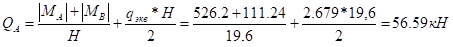
б) правая стойка:

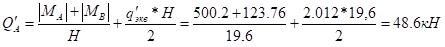
При правильном решении сумма поперечных сил внизу должна быть равна сумме всех горизонтальных нагрузок:

;

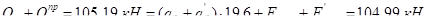
Строим эпюры:

Рис. 32. Эпюры M, Q, N от действия ветровой нагрузки