Задачи одномерной статистики (статистики случайных величин)

Сравнение математических ожиданий проводят в тех случаях, когда необходимо установить соответствие показателей качества изготовленной продукции и эталонного образца. Это — задача проверки гипотезы:

Н0: М (Х) = m0,.

где m0 — значение соответствующее эталонному образцу; Х — случайная величина, моделирующая результаты наблюдений. В зависимости от формулировки вероятностной модели ситуации и альтернативной гипотезы сравнение математических ожиданий проводят либо параметрическими, либо непараметрическими методами.

Сравнение дисперсий проводят тогда, когда требуется установить отличие рассеивания показателя качества от номинального. Для этого проверяют гипотезу:

Не меньшее значение, чем задачи проверки гипотез, имеют задачи оценивания параметров. Они, как и задачи проверки гипотез, в зависимости от используемой вероятностной модели ситуации делятся на параметрические и непараметрические.

В параметрических задачах оценивания принимают вероятностную модель, согласно которой результаты наблюдений x1, x2,…, xn рассматривают как реализации n независимых случайных величин с функцией распределения F (x;и). Здесь и — неизвестный параметр, лежащий в пространстве параметров и заданном используемой вероятностной моделью. Задача оценивания состоит в определении точечной оценок и доверительных границ (либо доверительной области) для параметра и.

Параметр и — либо число, либо вектор фиксированной конечной размерности. Так, для нормального распределения и = (m, у2) — двумерный вектор, для биномиального и = p — число, для гамма-распределения и = (a, b, c) — трехмерный вектор, и т. д.

В современной математической статистике разработан ряд общих методов определения оценок и доверительных границ — метод моментов, метод максимального правдоподобия, метод одношаговых оценок, метод устойчивых (робастных) оценок, метод несмещенных оценок и др.

Кратко рассмотрим первые три из них.

Метод моментов основан на использовании выражений для моментов рассматриваемых случайных величин через параметры их функций распределения. Оценки метода моментов получают, подставляя выборочные моменты вместо теоретических в функции, выражающие параметры через моменты.

В методе максимального правдоподобия, разработанном в основном Р. А. Фишером, в качестве оценки параметра и берут значение и*, для которого максимальна так называемая функция правдоподобия.

f (x1, и) f (x2, и) … f (xn, и),.

где x1, x2,…, xn — результаты наблюдений; f (x, и) — их плотность распределения, зависящая от параметра и, который необходимо оценить.

Оценки максимального правдоподобия, как правило, эффективны (или асимптотически эффективны) и имеют меньшую дисперсию, чем оценки метода моментов. В отдельных случаях формулы для них выписываются явно (нормальное распределение, экспоненциальное распределение без сдвига). Однако чаще для их нахождения необходимо численно решать систему трансцендентных уравнений (распределения Вейбулла-Гнеденко, гамма). В подобных случаях целесообразно использовать не оценки максимального правдоподобия, а другие виды оценок, прежде всего одношаговые оценки.

В непараметрических задачах оценивания принимают вероятностную модель, в которой результаты наблюдений x1, x2,…, xn рассматривают как реализации n независимых случайных величин с функцией распределения F (x) общего вида. От F (x) требуют лишь выполнения некоторых условий типа непрерывности, существования математического ожидания и дисперсии и т. п. Подобные условия не являются столь жесткими, как условие принадлежности к определенному параметрическому семейству.

В непараметрической постановке оценивают либо характеристики случайной величины (математическое ожидание, дисперсию, коэффициент вариации), либо ее функцию распределения, плотность и т. п. Так, в силу закона больших чисел выборочное среднее арифметическое является состоятельной оценкой математического ожидания М (Х) (при любой функции распределения F (x) результатов наблюдений, для которой математическое ожидание существует). С помощью центральной предельной теоремы определяют асимптотические доверительные границы.

(М (Х))Н =, (М (Х))В = .

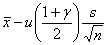
где г — доверительная вероятность, — квантиль порядка стандартного нормального распределения N (0;1) с нулевым математическим ожиданием и единичной дисперсией, — выборочное среднее арифметическое, s — выборочное среднее квадратическое отклонение. Термин «асимптотические доверительные границы» означает, что вероятности.

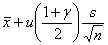
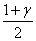
P{(M (X))H M (X)},.

P{(M (X))H < M (X) < (M (X))B}.

стремятся к, и г соответственно при n > ?, но, вообще говоря, не равны этим значениям при конечных n. Практически асимптотические доверительные границы дают достаточную точность при n порядка 10.

Второй пример непараметрического оценивания — оценивание функции распределения. По теореме Гливенко эмпирическая функция распределения Fn (x) является состоятельной оценкой функции распределения F (x). Если F (x) — непрерывная функция, то на основе теоремы Колмогорова доверительные границы для функции распределения F (x) задают в виде.

(F (x))Н = max, (F (x))B = min ,.

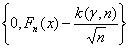
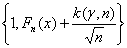
где k (г, n) — квантиль порядка г распределения статистики Колмогорова при объеме выборки n (напомним, что распределение этой статистики не зависит от F (x)).

Правила определения оценок и доверительных границ в параметрическом случае строятся на основе параметрического семейства распределений F (x;и). При обработке реальных данных возникает вопрос — соответствуют ли эти данные принятой вероятностной модели? Т. е. статистической гипотезе о том, что результаты наблюдений имеют функцию распределения из семейства {F (x;и), и И} при некотором и = и0? Такие гипотезы называют гипотезами согласия, а критерии их проверки — критериями согласия.

Если истинное значение параметра и = и0 известно, функция распределения F (x;и0) непрерывна, то для проверки гипотезы согласия часто применяют критерий Колмогорова, основанный на статистике.

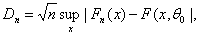
где Fn (x) — эмпирическая функция распределения.

Если истинное значение параметра и0 неизвестно, например, при проверке гипотезы о нормальности распределения результатов наблюдения (т.е. при проверке принадлежности этого распределения к семейству нормальных распределений), то иногда используют статистику.

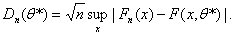
Она отличается от статистики Колмогорова Dn тем, что вместо истинного значения параметра и0подставлена его оценка и*.

Распределение статистики Dn (и*) сильно отличается от распределения статистики Dn. В качестве примера рассмотрим проверку нормальности, когда и = (m, у2), а и* = (, s2). Для этого случая квантили распределений статистик Dn и Dn (и*) приведены в табл.1. Таким образом, квантили отличаются примерно в 1,5 раза.

Таблица 1 — Квантили статистик Dn и Dn (и*) при проверке нормальности.

При первичной обработке статистических данных важной задачей является исключение результатов наблюдений, полученных в результате грубых погрешностей и промахов. Например, при просмотре данных о весе (в килограммах) новорожденных детей наряду с числами 3,500, 2,750, 4,200 может встретиться число 35,00. Ясно, что это промах, и получено ошибочное число при ошибочной записи — запятая сдвинута на один знак, в результате результат наблюдения ошибочно увеличен в 10 раз.

Статистические методы исключения резко выделяющихся результатов наблюдений основаны на предположении, что подобные результаты наблюдений имеют распределения, резко отличающиеся от изучаемых, а потому их следует исключить из выборки.

Простейшая вероятностная модель такова. При нулевой гипотезе результаты наблюдений рассматриваются как реализации независимых одинаково распределенных случайных величин X1, X2, , Xn с функцией распределения F (x). При альтернативной гипотезе X1, X2, , Xn-1 — такие же, как и при нулевой гипотезе, а Xn соответствует грубой погрешности и имеет функцию распределения G (x) = F (x — c), где с велико. Тогда с вероятностью, близкой к 1 (точнее, стремящейся к 1 при росте объема выборки),.

Xn = max { X1, X2, , Xn} = Xmax ,.

т.е. при описании данных в качестве возможной грубой ошибки следует рассматривать Xmax. Критическая область имеет вид Ш = {x: x > d}.

Критическое значение d = d (б, n) выбирают в зависимости от уровня значимости б и объема выборки n из условия.

P{Xmax > d | H0} = б (1).

Условие (1) эквивалентно при больших n и малых б следующему:

(2).

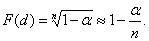
Если функция распределения результатов наблюдений F (x) известна, то критическое значение dнаходят из соотношения (2). Если F (x) известна с точностью до параметров, например, известно, что F (x) — нормальная функция распределения, то также разработаны правила проверки рассматриваемой гипотезы.

Однако часто вид функции распределения результатов наблюдений известен не абсолютно точно и не с точностью до параметров, а лишь с некоторой погрешностью. Тогда соотношение (2) становится практически бесполезным, поскольку малая погрешность в определении F (x), как можно показать, приводит к большой погрешности при определении критического значения d из условия (2), а при фиксированном d уровень значимости критерия может существенно отличаться от номинального.

Поэтому в ситуации, когда о F (x) нет полной информации, однако известны математическое ожидание М (Х) и дисперсия у2 = D (X) результатов наблюдений X1, X2, , Xn, можно использовать непараметрические правила отбраковки, основанные на неравенстве Чебышёва. С помощью этого неравенства найдем критическое значение d = d (б, n) такое, что.

(3).

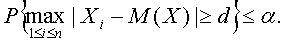
Так как.

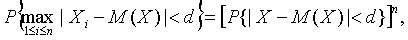
то соотношение (3) будет выполнено, если.

(4).

По неравенству Чебышёва.

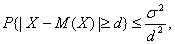
(5).

поэтому для того, чтобы (4) было выполнено, достаточно приравнять правые части формул (4) и (5), т. е. определить d из условия.

(6).

Правило отбраковки, основанное на критическом значении d, вычисленном по формуле (6), использует минимальную информацию о функции распределения F (x) и поэтому исключает лишь результаты наблюдений, весьма далеко отстоящие от основной массы. Другими словами, значениеd1, заданное соотношением (1), обычно много меньше, чем значение d2, заданное соотношением (6).