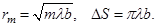Дифракция света. 
Принцип Гюйгенса-Френеля

Дифракция света. Принцип Гюйгенса — Френеля

По определению немецкого учёного Зоммерфельда дифракция — «любое отклонение распространения света от прямолинейного, не связанное с отражением или преломлением».

В более узком смысле дифракцией называют явление огибания волной препятствия (или проникновение света в область геометрической тени).

В теории волн под дифракцией понимают всю совокупность явлений в волновом поле, возникающих при наличии препятствий распространению волны.

Используя понятие интерференции света, можно сказать, что дифракция — это интерференция в ограниченных световых пучках.

Принципиальное значение дифракции состоит в том, что она, как и интерференция, доказывает волновую природу света. Дифракция имеет большое практическое значение, поскольку она ограничивает возможности концентрации света в пространстве, определяет предел разрешающей способности оптических приборов, влияет на формирование оптического изображения и т. п.

Первое сообщение о наблюдении дифракции света было сделано Гримальди (1665 г). Схема опыта представлена на рис. 4.1. Источник света S освещает отверстие в непрозрачном экране Э, а на плоскости П, расположенной позади экрана, измеряется освещенность. Гримальди установил, что изображение отверстия не имеет резкой границы. Этот результат не мог быть объяснён в рамках корпускулярной теории света, согласно которой свет должен распространяться прямолинейно.

Первое объяснение дифракции света было дано Френелем в 1818 г. В своём мемуаре он показал, что количественное описание дифракционных явлений возможно на основе принципа Гюйгенса, если его дополнить принципом интерференции вторичных волн. Кирхгоф в 1882 г. дал строгое математическое обоснование принципа Гюйгенса-Френеля.

В рамках электромагнитной теории света точное решение задачи о распространении света даётся на основе уравнений Максвелла с соответствующими граничными условиями, но сопряжено с большими математическими трудностями. В большинстве случаев, представляющих практический интерес, вполне достаточным оказывается приближённый метод решения задач дифракции, основанный на принципе Гюйгенса-Френеля.

Согласно принципу Гюйгенса, каждую точку, в которую пришла волна от источника, можно принять за центр вторичных волн, распространяющихся во все стороны. Френель дополнил принцип Гюйгенса предположением о том, что вторичные световые волны могут как усиливать, так и ослаблять друг друга, т. е. они могут интерферировать. Световое поле есть результат интерференции элементарных вторичных волн, испускаемых каждым элементом некоторой волновой поверхности — это утверждение составляет содержание принципа Гюйгенса-Френеля. Основываясь на этом принципе, Френель смог с большой точностью рассчитать распределение света в дифракционной картине, т. е. решить задачу дифракции.

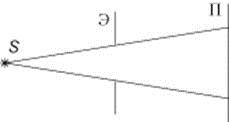
Р и с. 4.1 Р и с. 4.2.

Рассмотрим элементарную теорию дифракции света, построенную по принципу Гюйгенса-Френеля.

Сначала запишем математическую формулировку принципа Гюйгенса-Френеля. Введём некоторую поверхность X, охватывающую источник света S, и будем считать каждый элемент DS этой поверхности источником вторичной сферической световой волны (рис. 4.2). Амплитуда вторичной световой волны, достигающей интересующей нас точки P, должна быть пропорциональной амплитуде первичной волны Em, приходящей к элементу DS, а также площади самого элемента DS, и обратно пропорциональна расстоянию R от элемента DS до точки P.

Для определения результирующей амплитуды в точке P, т. е. суммы элементарных амплитуд, необходимо учесть, что колебания от разных элементов DS достигают точки P с разными фазами. Это приводит к появлению в выражении для результирующей амплитуды множителя cos (Kr + A), где K = 2P/L, а A — дополнительная фаза, равная фазе первичной волны на элементе DS, притом для разных элементов она в общем случае не одинакова.

Таким образом, результирующая амплитуда напряжённости E0 (P) в точке P может быть представлена как суперпозиция элементарных амплитуд с учётом их взаимных фазовых соотношений:

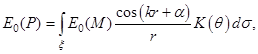
Где интегрирование проводится по всей поверхности, окружающей источник.

В интеграле K (Q) — некоторый «коэффициент наклона», учитывающий то обстоятельство, что вклад элемента DS в результирующее поле зависит от ориентации данного элемента поверхности по отношению к направлению на точку наблюдения.

Формулу можно записать через показательную функцию в виде:

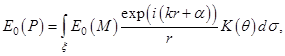
Где E0(P) и E0(M) — в общем случае комплексные амплитуды поля в точке P и в точке M соответственно.

Интеграл носит название интеграла Гюйгенса-Френеля. Формула построена на основе качественных физических соображений. Наиболее существенно то, что интеграл Гюйгенса-Френеля учитывает фазы элементарных вторичных волн, приходящих в точку P от различных элементов поверхности X, т. е. принимается во внимание интерференция вторичных волн.

Функция K (Q) в остаётся пока неопределённой. Френель полагал, что K (Q) монотонно убывает от некоторого начального значения K (0) до нуля при изменении Q от нуля до P/2. Как мы увидим дальше, многие практически важные задачи можно решить, не уточняя конкретного вида зависимости его от угла Q.

В дальнейшем будем рассматривать ситуации, позволяющие в качестве поверхности X брать волновую поверхность падающей волны, что значительно упрощает расчёты, например, в формуле дополнительную фазу A можно считать равной нулю, A = 0.

Зоны Френеля. Суммирование (интегрирование) амплитуд элементарных колебаний, приходящих в точку P, вообще говоря, весьма сложно. Но в простейших случаях, обладающих определённой симметрией, интегрирование, как показал Френель, может быть заменено простым алгебраическим или графическим сложением (последнее особенно наглядно).

Приближённый способ расчёта дифракционных картин основан на представлении о так называемых полуволновых зонах или зонах Френеля, на которые разбивается поверхность X, и конфигурация которых зависит от симметрии рассматриваемой задачи.

Если, например, источник S точечный, и волна изотропная, то удобно вспомогательную поверхность X выбрать в виде сферы радиуса A с центром в точке S (рис. 4.3).

Согласно принципу Гюйгенса-Френеля, данную поверхность можно рассматривать как источник вторичных световых волн с одинаковой начальной фазой. Выделим на сфере кольцевые зоны так, чтобы расстояния от границ зоны до точки наблюдения отличались на половину длины световой волны. Для этого из точки Р мысленно проводим сферы радиусами B, B+, B+2, … B+M.

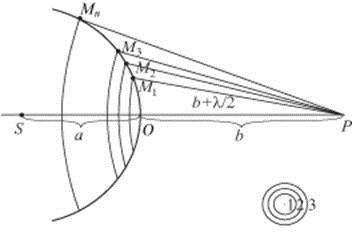
Р и с. 4.3.

Обозначая границы зон буквами M1, M2, M3, …, получим:

Где L — длина световой волны, P — точка наблюдения, O — центр первой зоны (рис. 4.3). Заметим, что положение границ френелевских зон зависит от выбора точки наблюдения. Смысл разбиения поверхности X на зоны состоит в том, что разность фаз элементарных вторичных волн, приходящих в точку наблюдения от данной зоны, не превышает величины P. Сложение таких волн приводит к их взаимному усилению. Поэтому каждую зону Френеля можно рассматривать как источник вторичных волн, имеющих определённую фазу. Напротив, две соседние зоны Френеля действуют как источники, колеблющиеся в противофазе.

Размеры зон Френеля. Для того, чтобы оценить относительный вклад френелевских зон в интеграл, оценим радиусы зон и их площади.

На рис. 4.4 показаны точечный источник света S, точка наблюдения поля P, часть сферической поверхности X (источника вторичных волн) и внешняя граница первой зоны Френеля. Пусть A — радиус сферы, B — кратчайшее расстояние от точки P до сферы, R — радиус первой световой зоны Френеля. Из рис. 4.4 видно, что: откуда запишем:

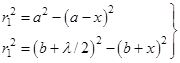
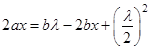
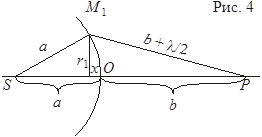
Как правило, в оптике справедливо приближение: ,.

Поэтому пренебрегая слагаемыми, которые пропорциональны L2 и X2, получим из и :

,.

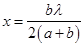
Откуда:. Аналогичным образом находим внешний радиус M-й зоны Френеля:

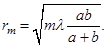
Площади зон (при достаточно малых M): или.

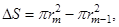
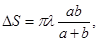
Т. е. практически одинаковы. Но амплитуды колебаний, приходящих в точку P от зон, монотонно и слабо убывают из-за увеличения расстояния R до точки P от каждой следующей зоны и роста угла Q между нормалью к элементам зоны и направлением на точку P.

Физическое содержание задачи почти не измениться, а формулы станут проще, если вместо сферической волны точечного источника рассмотреть плоскую световую волну. В данном случае зоны Френеля представляют собой кольца на плоскости. Их радиусы и площади можно подсчитать по формулам и, полагая A ® Ґ. Получим: