Геометрия манипулятора вида 5вп-1

Геометрия манипулятора вида 5вп-1

На рисунке 1 изображена в аксонометрии кинематическая схема семизвенного манипулятора с пятью вращательными и одной поступательной парами. Стойка представлена координатными осями Oxyz и является первым звеном манипулятора. Второе звено (ОА,) образует со стойкой первую вращательную пару, вдоль оси которой направлены орт и ось Оz. Третье звено (AB,) образует со вторым звеном вторую вращательную пару, вдоль оси которой направлен орт перпендикулярный к отрезкам ОА и AB. Четвертое звено (ВС,) с третьим образует третью вращательную пару, вдоль оси которой направлен орт, параллельный и перпендикулярный к AB, ВС. Пятое звено (CD,) с четвертым составляет четвертую вращательную пару, вдоль оси которой направлен орт. параллельный и перпендикулярный ВС, CD. Шестое звено изогнуто под прямым углом, а потому изображается двумя взаимно перпендикулярными отрезками DE и EF, один из которых (DE) расположен на одной прямой с отрезком CD. Шестое звено DEF образует с пятым пятую вращательную пару, вдоль оси которой направлен орт, расположенный на одной прямой с точками С, D, Е. Седьмое звено FN с шестым образует поступательную пару, обеспечивающую перемещение точки N вдоль прямой ЕF. Седьмое звено называется конечным или рабочим, так как на нем устанавливается вспомогательный механизм с инструментом для выполнения производственного задания. С конечным звеном соединена координатная система N_x6y6z6. Ось Nx₆ расположена на продолжении отрезка FN, а ось Nz₆ параллельна орту. Ось Ny₆ направлена так, чтобы образовалась правая прямоугольная координатная система N_x6y6z6.

Постоянными параметрами данного манипулятора являются указанные выше условия относительного расположения отрезков и ортов, а также длины звеньев: r₁=OA; r₂=AB; r₄=CD; r₅=DE; r₆=EF. Механизм имеет шесть независимых переменных параметров: ц₁ — угол поворота второго звена относительно стойки; ц₂ — угол поворота третьего звена относительно второго; ц₃ — угол поворота четвертого звена относительно третьего; ц₄ — угол поворота пятого звена относительно четвертого; ц₅ — угол поворота шестого звена относительно пятого: р — переменная длина отрезка FN.

Кроме того, рассмотрим шесть переменных параметров конечного звена относительно стойки: три координаты точки N и три независимых угла ш, ?, ц поворота конечного звена вокруг полюса N.

Для исследования геометрии манипулятора использован графоаналитический метод. Допустим, что известны постоянные параметры данного манипулятора и заданы конкретные значения его переменных параметров: ц₁, ц₂, ц₃, ц₄, ц₅, p. На рисунке 2 построены по этим данным ортогональные проекции кинематической схемы исследуемого манипулятора. Для построений использованы в пространстве шесть плоскостей проекций: первая, параллельная хОу; вторая, параллельная xOz; третья, параллельная плоскости ломаной OABCD; четвертая, перпендикулярная к третьей и орту; пятая, перпендикулярная к первой и параллельная шестая, перпендикулярная к Nx₆.

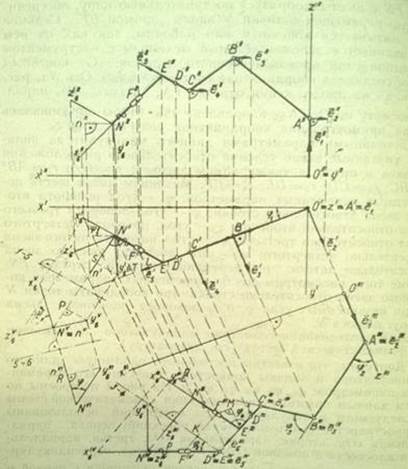
Рисунок 2 — Ортогональные проекции кинематической схемы.

Ортогональные проекции кинематической схемы манипулятора являются логической схемой для вывода аналитических зависимостей между его параметрами. На чертеже каждый параметр исследуемого манипулятора проецируется без искажения хотя бы ни одну из плоскостей проекций.

Ортогональные проекции кинематической схемы манипулятора являются логической схемой для вывода аналитических зависимостей между его параметрами. На чертеже каждый параметр исследуемого манипулятора проецируется без искажения хотя бы ни одну из плоскостей проекций.

Прямая задача геометрии манипулятора заключается в определении переменных параметров конечного звена по заданным постоянным параметрам манипулятора и значениям ц₁, ц₂, ц₃, ц₄, ц₅, p.

В результате графоаналитического решения прямой задачи с помощью рисунка 2 получены формулы:

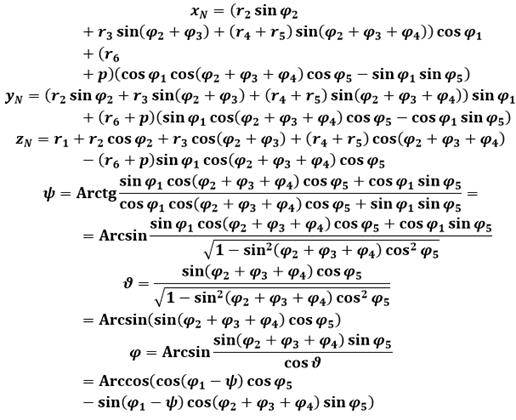
Обратная задача геометрии манипулятора заключается в определении шести независимых переменных параметров ц₁, ц₂, ц₃, ц₄, ц₅, p по заданным постоянным параметрам манипулятора и значениям шести параметров его конечного звена.

Наметим план решения обратной задачи в пространстве. По данным шести параметрам конечного звена строим в координатной системе O_xyzточку N и отрезки положительных полуосей Nx₆y₆z₆. Продлеваем ось Nx₆ до пересечения в точке Е с плоскостью у, проходящей через Oz и параллельной Nz₆. В плоскости, а через точку Е проводим параллельно Nz₆ отрезок ЕС, равный r₄+r₅. В плоскости у строим точку А, расположенную на положительной полуоси Oz и удаленную от O на r₁, и точку B, расстояние которой до A равно r₂, а до C равно r₃. При этом получаются два положения точки В, одно из которых можно отбросить в зависимости от конструкции манипулятора. Точка D расположена на отрезке СЕ и делит его на части: CD=r₄ и DE=r₅. Параметр p получается путем вычитания величины r₆ из длины построенного отрезка NE. Угол ц₁ определен положением плоскости у, углы ц₂, ц₃, ц₄ положением ломаной OABCD, а угол ц₅ — относительным положением плоскости треугольника DEN и плоскости у.

План решения обратной задачи графически осуществлен на рисунке 2, а затем переведен на аналитический язык. Результаты графических построений позволили проверить выведенные формулы:

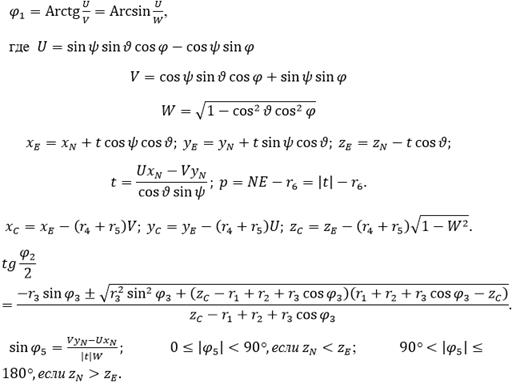
С помощью формул, решающих прямую и обратную задачи геометрии данного манипулятора, можно программировать и автоматизировать его работу.

манипулятор геометрия звено пространство.

• 1. Ананов Г. Д" Смирнов Д. М. Классификация манипуляторов. — «Труды ЛИТМО», 1974, вып. 77, с. 64— 70.
• 2. Ананов Г. Д. Кинематика пространственных шарнирных механизмов сельскохозяйственных машин. М.—Л., Машгиз, 1963.