Конденсаторный метод измерения диэлектрической проницаемости

Измерения в данной работе проводились с использованием конденсаторного метода. На рисунке 5 представлена полная эквивалентная схема измерительного конденсатора.

Рисунок 5 — Эквивалентная схема измерительного конденсатора [2].

Где: С0 — активная ёмкость (емкость возникающая непосредственно в объеме исследуемого материала); С1 — краевые поля и ёмкость между обкладками;

С2 — ёмкость зазоров между обкладками и диэлектриком; L — самоиндукция проводов подключения; R — потери энергии в измеряемом диэлектрике.

С0, С1, С2 называются константами конденсатора, в случае если при внесении материала в конденсатор их значения не изменяются. На практике же, при внесении материала в конденсатор, происходит изменение полей, что очень затрудняет получение истинных результатов и приводит к ошибкам вычислений, поэтому параметры С1, С2 и L принято называть паразитными. Задача состоит в сведении к минимуму их влияния. Этого можно добиться следующими способами. На рисунке 6 изображена схема плоского дискового конденсатора.

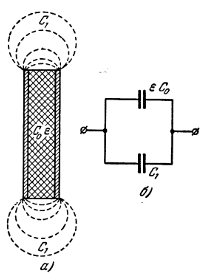
а) конденсатор с образцом, б) эквивалентная схема Рисунок 6 — Плоский дисковый конденсатор [2].

Плотно прижатые к диэлектрику обкладки конденсатора дают С2 = ?, тогда эквивалентная схема выглядит следующим образом, как на рисунке 6. Для этого на образец наносят электроды, тип и состав которых зависит от исследуемого материала.

Изменение С0 и С1 можно сделать незначительным при С0>>С1, это осуществляется у конденсаторов с диаметром обкладок много больше расстояния между ними D>>d. Однако этот подход приводит к нежелательным последствиям в виде слишком больших регистрируемых величин. Поле конденсатора с обкладками бесконечной длины однородно при наличии в нем шайбы диэлектрика, поэтому для снижения влияния краевых полей используются конденсаторы с частичным заполнением. На рисунке 7 изображен плоский конденсатор с обкладками бесконечного радиуса.

В случае с жидкостями внутрь конденсатора вклеивается кольцо из подходящего материала. При малом радиусе образца диэлектрика R0 по сравнению с диаметром обкладок, С0 может быть определено с высокой точностью. Так, что зная емкость пустого и заполненного конденсатора, по формулам (4), (5) и (6) мы можем рассчитать ДП.

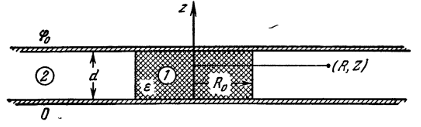
Рисунок 7 — Плоский конденсатор с обкладками бесконечного радиуса.

(4).

(5).

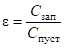
(6).

где Спуст — емкость пустого конденсатора;

Сзап — емкость заполненного конденсатора.

На рисунке 8 показан — измерительный конденсатор с частичным заполнением. То есть в этом случае С0 не меняется с введением образца.

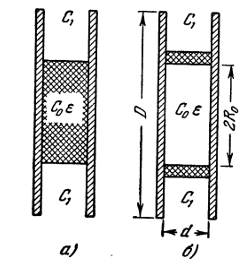
а) для твёрдых образцов, б) для жидкостей Рисунок 8 — Измерительный конденсатор с частичным заполнением [2].

Для измерительного конденсатора должны выполняться условия квазистационарности. Эффективные размеры конденсатора должны быть меньше длины волны высокочастотного поля. Это накладывает ограничения на геометрические размеры конденсатора и величину ДП.

Рисунок 9 — Распределение амплитуды напряжения в конденсаторе, питаемом током высокой частоты [2].

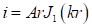
Рассмотрим заполненный диэлектриком плоский дисковый конденсатор (рисунок 9). Для тока смещения i, текущего через цилиндр радиуса r, и напряжения U между обкладками на расстоянии r от центра конденсатора можно получить выражения;. Где, А и В некоторые постоянные, зависящие от геометрических размеров конденсатора, r — расстояние от центра конденсатора по радиусу, — волновое число, и функции Бесселя нулевого и первого порядка соответственно. Как видно из последнего выражения, амплитуда напряжения между обкладками конденсатора изменяется в соответствии с законом изменения функции, проходя через ряд нулевых значений по мере увеличения расстояния от центра конденсатора. Находя нули функции, можно определить радиусы узловых окружностей напряжения, т. е. геометрические места точек, в которых амплитуда напряжения между обкладками равна нулю.

Для радиуса первой узловой окружности получим соотношение (7):

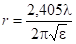
. (7).

из которого можно вывести условие квазистационарности конденсатора, заполненного диэлектриком. Выбирая радиус реального измерительного конденсатора значительно меньше радиуса первой узловой окружности, будем иметь между обкладками такого конденсатора приблизительно постоянное напряжение (при перемещении по радиусу), что и дает возможность рассматривать его как квазистационарный. При получим для радиуса квазистационарного конденсатора выражение:

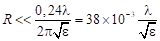
(8).

которое позволяет для любых значений л и е, выбрать размеры конденсатора.

Для подключения измерительного конденсатора часто используются волноводные или коаксиальные линии. На высоких частотах трудно учесть изменение индуктивности L и потерь в проводниках, что приводит к ошибкам вычислений. Поэтому исследуемый образец должен входить в установку как органическая её часть, без проводов.

Таким образом, исключив все паразитные параметры, мы можем представить следующую эквивалентную схему, рисунок 10.

Рисунок 10 — Эквивалентная схема измерительного конденсатора [2].

На рисунке 10: С — емкость всего конденсатора, R — сопротивление эквивалентное потерям энергии в образце Отсюда можем определить ДП по формуле (9):

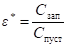
(9).

где е* комплексная диэлектрическая проницаемость, вычисляемая по формуле (10):

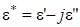
(10).

где.

— характеризует действительную величину ДП материала;

— характеризует потери энергии в диэлектрике.

В нашем случае из формулы (9) имеем:

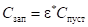
. (11).

Для вычисления комплексной ДП (,) мы будем использовать измеренные нами величины R, С и щ, а следовательно нужно представить действительную и мнимую части комплексной ДП как функции, зависящие от этих величин: .

Комплексное емкостное сопротивление конденсатора равно, формула (12):

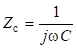
. (12).

Для параллельной цепи, представленной на рисунке 10, имееем, уравнение вида (13):

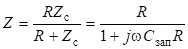
. (13).

Разделив действительную и мнимую части получим выражение (14):

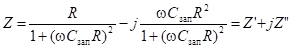
. (14).

С другой стороны, используя выражение (11) получим соотношения (15) и (16):

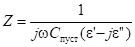
(15).

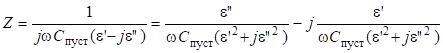
(16).

Приравниваем мнимые и действительные части формул (14) и (16):

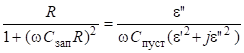
(17).

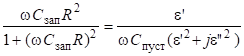
. (18).

Поделив выражение (17) на (18) получим:

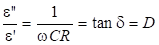
. (19).

Что соответствует выражению для тангенса угла диэлектрических потерь. Отсюда:

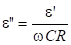
. (20).

Тогда для е' получим:

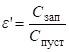
. (21).

Таким образом, используя данный метод измерения, мы можем достаточно точно измерить ДП материала.