Анализ плоских волн методами геометрической оптики

Рассмотрим основы метода приближенного решения уравнения Гельмгольца, который применяют в том случае, когда длина волны пренебрежимо мала по сравнению с любыми характерными размерами неоднородностей материальной среды. При этом уравнение (3.82) заведомо справедливо. Для этого приближения используют термин геометрическая оптика, поскольку описанная ситуация типична прежде всего для оптического диапазона волн. Однако этим методом удается эффективно решать многие задачи, связанные, например, с распространением радиоволн в ионосфере и тропосфере Земли, а также исследовать такие неэлектромагнитные волновые процессы, как распространение звуковых волн в Океане, движение сейсмических волн в земной коре и распространение света в волоконно-оптических световодах.

Считая, что потери в среде отсутствуют, вместо постоянной распространения используем волновое число. Запишем обобщенное уравнение для проекций вектора на координатные оси, обозначив обобщенную проекцию символом. Из (3.82) получим:

. (3.83).

где n2® = - квадрат локального значения коэффициента преломления неоднородной среды, 02 = 2 — квадрат волнового числа для вакуума, а г — радиус-вектор точки наблюдения.

В основе метода геометрической оптики лежит интуитивное представление о том, что в пределах малой окрестности любой точки наблюдения волновой процесс представляет собой локально-плоскую волну, которая может быть описана выражением.

® = Аexp{-i0L®}. (3.84).

Здесь L® — уравнение поверхности, на которой фаза электромагнитной волны постоянна, неизвестная пока функция пространственных координат, которую называют эйконалом. Эйконал имеет размерность длины. В случае плоской волны, распространяющейся в однородной среде вдоль оси z, в качестве эйконала выступает плоскость перпендикулярная оси z.

Уравнение эйконала.

Чтобы найти функцию L (x у z), подставим (3.84) в (3.83).

. (3.85).

Учтем, что лапласиан это дивергенция от градиента, и преобразуем выражение для лапласиана.

(3.86).

В правой части равенства записана дивергенция от произведения скаляра на вектор. Как известно из векторного анализа (см. П2.19), для скаляра и вектора справедливо равенство:

Полагая =, а, преобразуем выражение для лапласиана (3.86).

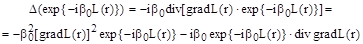
Теперь подставим выражение для лапласиана в (3.85).

Учтем, что в рамках метода геометрической оптики длина волны стремится к нулю, и поэтому волновое число 0 стремится к бесконечности. Второе слагаемое пропорционально 0, а два другие — 02, поэтому вторым слагаемым в левой части последнего равенства можно пренебречь. После сокращения на общий множитель приходим к уравнению.

(grad L®)2 = n®2; | grad L® | = ± n® (3.87).

Это нелинейное дифференциальное уравнение в частных производных первого порядка и называют уравнением эйконала. Уравнение является основным соотношением геометрической оптики пространственно неоднородной среды. Отметим следующие важные факты.

• * В уравнение эйконала не входит длина волны. Поэтому метод геометрической оптики не учитывает каких-либо дифракционных эффектов и явлений интерференции волн.
• * Метод геометрической оптики справедлив лишь в том случае, когда n®>0 во всех точках пространства. Дело в том, что уравнение Гельмгольца с отрицательным вторым слагаемым левой части имеет совершенно другое решение.

Рассмотрим, как будет выглядеть эйконал в различных частных случаях. Сначала проведем расчет для плоской волны в однородной среде. Уравнение (3.87) в этом случае выглядит так.

| grad L | = n = const.

решение этого уравнения:

. (3.88).

Получено обычное выражение для комплексной амплитуды плоской волны, распространяющейся вдоль ось z. Для однородной среды эйконал — плоскость, перпендикулярная направлению распространения.

Теперь пусть волна по-прежнему распространяется вдоль оси z, и показатель преломления изменяется с ростом z. n =n (z).Уравнение эйконала будет выглядеть так.

dL/dz = n (z).

решение этого уравнения:

(3.89).

Знак ±, стоящий перед интегралом говорит о том, что при положительном n возможны прямая и обратная волны, а суммарное поле будет их суперпозицией. Выражение (3.88) аналогично (3.89). И в том и в другом случае эйконал — плоскость перпендикулярная направлению распространения, но в первом случае эйконал зависит от z линейно, а во втором — нелинейно.

Особая ситуация возникает тогда, когда в некоторой точке z0 показатель преломления обращается в нуль. Пусть, например, при zz0 отрицателен. Распространяется только падающая волна. В самой точке z0 и в ее малой окрестности метод геометрической оптики теряет силу, однако ясно, что правее нее волновой процесс будет отсутствовать. Поскольку в среде нет потерь, падающая волна целиком отражается назад. Рассмотренную здесь точку принято называть точкой поворота.

Уравнение лучей.

Чтобы описать волновой процесс в приближении геометрической оптики, достаточно располагать семейством поверхностей постоянных фаз L (x, y, z)=const, которое образовано решениями уравнения эйконала. При этом можно задаться какой-либо начальной поверхностью, а затем, интегрируя уравнение эйконала, построить другие поверхности.

На практике предпочитают вместо совокупности поверхностей равных фаз строить лучевую картину поля, более традиционную и наглядную. Лучи образуют семейство линий, ортогональных к волновым фронтам. Вектор, касательный к лучу в некоторой точке пространства, указывает направление перемещения волнового фронта локально-плоской волны. Отсюда следует, что касательная к лучу ориентирована вдоль вектора grad L, указывающего направление наибыстрейшего изменения эйконала в пространстве и направление, вдоль которого распространяется электромагнитная волна.

Рассмотрим какой-нибудь конкретный луч. Пусть — радиус-вектор выбранной точки на луче, a s® —длина кривой, отсчитываемая вдоль луча. Направление вдоль кривой задается градиентом эйконала.

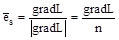
(3.90).

Выразим единичный вектор вдоль луча в прямоугольной системе координат через направляющие косинусы.

(3.91).

Приравнивая правые части равенств, получим дифференциальное уравнение луча.

. (3.92).

Это одна из форм уравнения луча. Некоторое неудобство уравнения (3.92) состоит в том, что правая часть его содержит эйконал L. Однако уравнение можно преобразовать таким образом, чтобы в правую часть входило только пространственное распределение показателя преломления n (г), известное заранее. Действительно, дифференцируя обе части уравнения (3.92) по переменной s получим.

.

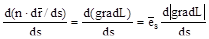
Преобразуем правую часть, воспользовавшись уравнением эйконала (3.87).

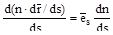
(3.93).

и получим векторное уравнение луча, выраженное через показатель преломления, которое эквивалентно системе трех дифференциальных уравнений в проекциях:

d/ds (n dx/ds) = dn/dx; d/ds (n dy/ds) = dn/dy; d/ds (n dz/ds) = dn/dz. (3.94).

Уравнения (3.93) или (3.94) дают возможность решить основную задачу геометрической оптики — построить лучевые траектории. Для этого необходимо прежде всего задаться точкой входа луча (х0, у0, z0) и начальным направлением лучевого вектора, т. е. тремя производными (dx/ds, dy/ds, dz/ds), которые представляют собой направляющие косинусы лучевого вектора в исходной точке. Строя шаг за шагом интегральную кривую, приходим в точку выхода луча.

Таким образом, создав в одной точке пространства плоскую волну с заданным направлением лучевого вектора, мы получаем в другой точке пространства также плоскую волну, у которой направление распространения будет, вообще говоря, уже другим. Построив лишь один луч, мы не получаем никаких сведений об амплитудах волн на входе и выходе, а построив семейство лучей, получим сгущение лучей в тех сечениях, в которых амплитуда поля растет, и разряжение, где падает.

Простейший случай — распространение плоских волн в однородной среде, для которой n = const и поэтому grad n = 0. Из (3.93) следует, что здесь d/ds2 = 0, откуда г = sa + b, где, а и b —некоторые постоянные векторы. Луч представляет собой прямую линию.

Наклонные лучи в среде с показателем преломления, изменяющимся по вертикали. Простейшая математическая модель распространения достаточно коротких электромагнитных волн в неоднородной атмосфере Земли или в градиентном световоде в рамках метода геометрической оптики сводится к решению уравнений лучей (3.94) при условии, что показатель преломления среды зависит только от вертикальной координаты z. Будем считать, что распространение происходит в плоскости xoz. При этом dy/ds=0. Поскольку показатель преломления зависит только от z, первое уравнение из системы (3.94) приобретает вид.

d/ds (n dx/ds) = 0. (3.95).

Отсюда следует, что.

dx/ds =C/n, (3.96).

где C — постоянная величина, которую можно определить исходя из того, что производная dx/ds является направляющим косинусом лучевого вектора по отношению к оси х. Если источник волн расположен в точке с координатами х = 0, z = z0 и луч в точке входа образует угол 0 с осью z, то С/n (z0) = sin0, C =n (z0)sin0. (3.97).

Чтобы получить уравнение траектории луча в явном виде, следует учесть, что второй из направляющих косинусов, то есть проекция единичного вектора на ось z может быть найдена по теореме Пифагора.

dz/ds= ± [l — (dx/ds)2]½ = ±[l-(С/n)2 ]l/2. (3.98).

Здесь положительный знак отвечает восходящей, а отрицательный — нисходящей ветви луча. Разделив (3.96) на (3.98), получаем дифференциальное уравнение кривой.

dx/dz = ± [(n/С)2-l]-½, (3.99).

решение которого.

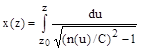
. (3.100).

При численных расчетах по этой формуле следует (в необходимых случаях) изменять знак перед корнем, переходя с восходящей на нисходящую ветвь луча.

Выражение (3.97) справедливо при любых значениях z.

n (z0) sin0 = n (z) sin. (3.101).

Это непосредственно следует из (3.96), если учесть, что при заданном z, sin = dx/ds. Если показатель преломления с ростом координаты z увеличивается, т. е. n (z) > n (z0), то в соответствии с (3.101) угол < 0 и луч искривляется вверх, стремясь стать более вертикальным. Наоборот, если n (z) 0 и луч искривляется вниз. В физике искривление траектории луча из-за изменения показателя преломления называют рефракцией. Общее правило таково: луч отклоняется в ту сторону, где оптическая плотность среды, выше.

Если показатель преломления с ростом высоты уменьшается, то возможна ситуация, когда = /2, т. е. происходит поворот луча. Это эквивалентно отражению волны от идеально проводящей плоскости. Точка поворота располагается на высоте zn, в которой угол = 900, sin = 1 и.

n (zn) = n (z0)sin0. (3.102).

Если значение 0 близко к /2, т. е. луч входит в неоднородную среду почти горизонтально, достаточно весьма небольшого уменьшения показателя преломления с высотой, чтобы произошел поворот луча. Описанные здесь явления играют существенную роль в распространении радиоволн вблизи поверхности Земли и светового луча в световоде.

Задачи и упражнения

• 1. Плоская электромагнитная волна с частотой 80 мегагерц распространяется в материальной среде без потерь и имеет длину волны 0,7 м. Вычислите фазовую скорость этой волны. Определите, на каком расстоянии фаза волны изменится на 2700, 5000.
• 2. Плоская волна распространяется в сторону увеличения z и имеет комплексную амплитуду (z) = 200 exp (-z), где = (0.3 + i0,5)м-1. Угловая частота волнового процесса = 8104с-1. Найдите мгновенное значение магнитного поля в плоскости z = 5 м, при t = 10−4с.
• 3. Погонное затухание плоской волны составляет 0,45 дБ/м. Определите, на каком расстоянии амплитуда волны уменьшится в 106 раз по сравнению с начальным уровнем.
• 4. Однородная плоская электромагнитная волна, гармонически изменяющаяся во времени, распространяется в среде без потерь с = 1, = 4. Амплитуда вектора электрического поля составляет 30 В/м. Определите амплитуду вектора напряженности магнитного поля и модуль среднего значения вектора Пойнтинга.
• 5. Плоская однородная электромагнитная волна распространяется в вакууме. Плотность потока мощности составляет 0,6 вт/м2. Вычислите амплитуду векторов электрической и магнитной индукции, напряженности электрического и магнитного полей.
• 6. Найдите волновое число и постоянную распространения плоской волны в среде с параметрами э = 2105См/м, = 2, = 3 на частоте 1МГц.
• 7. Найдите коэффициент ослабления плоских волн в диэлектрике с параметрами tg = 410−4, = 2; = 1.
• 8. Плоская линейно поляризованная волна распространяется в диэлектрике с потерями. э = 10−2См/м, = 10, = 108 1/с. Амплитуда напряженности электрического поля в начале координат составляет 510−3в/м. Рассчитать комплексную амплитуду электрического и магнитного полей, мгновенное и среднее значение вектора Пойнтинга, волновое число и постоянную затухания, длину волны и фазовую скорость волнового процесса.
• 9. По условию задачи 3.8 рассчитать плотности токов проводимости и смещения. Найти отношение их амплитуд. Сравнить фазы.
• 10. По условию задачи 3.8 рассчитать, на каком расстоянии от начала координат электрическое поле составит один процент от того значения, которое оно имело в начале координат.
• 11. Определить постоянную распространения, постоянную затухания, волновое число, волновое сопротивление среды, фазовую скорость и длину волны для среды с параметрами = 81, = 1, э = 0,1 См/м на следующих частотах: а) f = 105Гц, б) f = 108Гц, в) f = 1010Гц.
• 12. Условно можно считать, что если отношение плотности тока смещения к плотности тока проводимости больше 100, то среда — диэлектрик, а если это отношение меньше 0,01, то среда — проводник. Для данных задачи 3.11 определите, в каком из трех случаев среда — проводник, а в каком — диэлектрик.
• 13. Для случая рассмотренного в задаче 3.11, составьте выражения мгновенных значений векторов поля и, если среда не ограничена и плоская гармоническая линейно поляризованная волна распространяется вдоль оси z. При t = 0 и х = у = z = 0 Еm = 5В/м. Электрическое поле направлено по оси х.