Случай малых вероятностей

Рассмотренные выше методы анализа медицинских данных (доверительного оценивания доли (вероятности) и проверки однородности вероятностей) основаны на предположении о возможности использования биномиальной модели выборки. Кроме этого, необходимо, чтобы объем выборки n был достаточно большим — несколько десятков или сотен.

Наконец, кроме биномиальной модели и большого объема выборки, необходимо выполнение третьего условия: число m ответов «есть» (в схеме с двумя ответами «есть» — «нет») также было достаточно большим, сравнимым с объемом выборки. Последнее эквивалентно предположению, что np — произведение числа опытов на вероятность рассматриваемого ответа при отдельном опыте — также достаточно велико (np — среднее значение (математическое ожидание) числа ответов m, т. е. М (m) = np). Третье условие означает, что вероятность р не является слишком малой (не меньше 5−10%). Не должна быть слишком малой и дополнительная вероятность 1 — р. Следовательно, вероятность ответа «есть» должна лежать между 5 и 95% (а лучше — между 10 и 90%).

Однако последнее условие выполнено отнюдь не всегда. Например, в области с миллионным населением наблюдаются сотни или тысячи заболеваний. Хотя их число достаточно велико, но оно составляет лишь доли процента от численности населения. Для статистического моделирования в таких случаях используют не биномиальное распределение, а распределение Пуассона.

Случайная величина Y имеет распределение Пуассона, если.

.

где л — параметр распределения Пуассона (интенсивность заболеваемости или иной характеристики), P (Y=y) =0 для всех прочих чисел y.

Для распределения Пуассона математическое ожидание и дисперсия совпадают с интенсивностью:

M (Y) = л; D (Y) = л. (1).

Это распределение названо в честь французского математика С. Д. Пуассона (1781 — 1840), впервые получившего его в 1837 г. Распределение Пуассона — предельный случай биномиального распределения, когда вероятность р осуществления события мала, а число испытаний n велико, причем np = л. Таким образом, справедливо предельное соотношение.

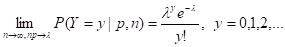
Поэтому распределение Пуассона (в старой терминологии «закон распределения») часто называют также «законом редких событий» .

Состоятельной оценкой неизвестного параметра л распределения Пуассона является наблюдаемое значение случайной величины Y. Доверительное оценивание может быть основано на асимптотической нормальности распределения Пуассона и соотношении (1). Для = 0,95 нижняя доверительная граница имеет вид л_нижн = Y — 1,96 ,.

а верхняя доверительная граница л_верх = Y + 1,96 .

Эти границы являются приближенными (асимптотическими), поскольку получены в предположении, что интенсивность л достаточно велика (несколько десятков или сотен). Более точные расчеты можно провести по правилам, приведенным в специальной литературе [10].

Пример 5. Пусть в муниципальном образовании численностью 125 тыс. чел. наблюдается 438 случаев заболевания. Необходимо оценить заболеваемость (на 10 000 жителей).

Заболеваемость составляет.

случаев на 10 000 жителей. Чтобы рассчитать доверительные границы, найдем границы для общей заболеваемости (для всего муниципального образования):

л_нижн = 438 — 1,96 = 438 — 41 = 397, л_верх = 438 + 41 = 479.

Нижняя доверительная граница для заболеваемости на 10 000 жителей составляет.

л_нижн = ,.

а верхняя доверительная граница для заболеваемости на 10 000 жителей:

л_верх = .

Есть ли отличия между двумя муниципальными образованиями, близкими по численности, или заболеваемости на одной и той же территории, но в соседние годы?

Следует рассматривать случайные величины Y₁ и Y₂, имеющие распределения Пуассона с параметрами л₁ и л₂ соответственно, и проверять статистическую гипотезу о равенстве параметров этих распределений, т. е. гипотезу однородности H₀: л₁ = л₂, при альтернативной гипотезе о наличии эффекта H₁: л ₁ л _2. (Иногда представляют интерес и иные альтернативные гипотезы, прежде всего односторонние альтернативные гипотезы и .).

В прикладной математической статистике разработаны правила проверки гипотезы однородности для распределений Пуассона [10, п. 5.5].

При достаточно больших (не менее нескольких десятков) наблюдаемых значениях случайных величин Y₁ и Y₂ достаточно воспользоваться статистическим критерием, основанным на асимптотической нормальности случайных величин с распределениями Пуассона.

В этом случае правило принятия решения при проверке однородности двух выборок формулируется следующим образом.

1. Вычислить статистику.

.

2. Сравнить значение статистики R с граничным значением K. Если R K, то принимается гипотеза однородности H0. Если же R > K, то однородность отсутствует и принимается альтернативная гипотеза H1 о наличии эффекта. Граничное значение К определяется выбором уровня значимости статистического критерия проверки однородности. В клинико-статистических и медико-биологических исследованиях обычно, а К = 1,96.

Примечание. Если численности сравниваемых популяций сильно отличаются, то необходимо применять более сложные способы расчета, описанные в статистической литературе [10, п. 5.5]. При этом исходная гипотеза однородности состоит в равенстве заболеваемости на 10 000 жителей. В нулевой гипотезе утверждается, что отношение параметров двух распределений Пуассона равно известной величине (отношению численностей популяций).

Пример 6. Пусть в 2009 г. на некоторой территории было 235 случаев заболевания, а в 2010 г. — 312 случаев. Можно ли объяснить это различие случайными причинами?

Примем, что за год численность населения на этой территории изменилась незначительно. Поскольку численность измеряется миллионами человек, то число заболеваний в определенном году моделируется распределением Пуассона.

Рассчитаем значение статистики критерия проверки однородности двух распределений Пуассона:

.

При = 0,05 K = 1,96 R = 3,29 > K = 1,96, поэтому гипотезу однородности отклоняем. При = 0,01 K = 2,58 R = 3,29 > K = 2,58. Можно сделать вывод о значительном увеличении заболеваемости.

Пример 7. Пусть выполнены все предположения примера 6, кроме одного — заболеваемость в 2010 г. составила 270 случаев. Изменятся ли сформулированные выводы?

Рассчитаем значение статистики критерия.

.

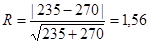
При = 0,05 K = 1,96 R = 1,56 < K = 1,96, следовательно, гипотезу однородности принимаем. Выводы примера 6 не подтверждаются. Различие между годами можно объяснить случайными причинами.

Расскажем о прикладном исследовании, в котором использовался метод проверки гипотезы о равенстве параметров двух распределений Пуассона.

Описторхоз — тяжелое глистное заболевание, склонное к хроническому течению, вызывающее нарушения различных функций организма [11, 12]. Один из путей заражения — употребление в пищу сырой рыбы, например, в замороженном (строганина) или вяленом виде, поэтому описторхоз распространен в северных районах, но встречается практически во всех субъектах РФ. Он приводит к серьезным осложнениям вплоть до развития первичного рака печени. Например, в одной из северных областей, где широко распространено заболевание описторхозом, количество заболеваний раком печени в 7 раз превышает средний показатель по стране. За год в России регистрируется около 100 тыс. лиц, заболевших описторхозом.

Анализировались статистические данные о заболеваемости описторхозом по 61 административной территории. Одна из основных задач исследования — отличить территории с наличием местных очагов заражения от территорий, где имеются лишь «завозные» случаи описторхоза. (Если пациент заболел, находясь на одной территории, а лечиться стал после переезда на другую, то наблюдаем «завозной» случай.) Другая задача — прогноз (с помощью доверительных границ) числа заболеваний на будущий год. Третья — типология (классификация) территорий по степени зараженности описторхозом.

Для решения поставленных задач использовались статистические модели и методы доказательной медицины, основанные на доверительном оценивании и проверке гипотез относительно параметров пуассоновских распределений. Число заболеваний на конкретной административной территории моделировалось распределением Пуассона. Изменение числа заболеваний с течением времени может быть связано с появлением очага заражения на рассматриваемой территории, но может объясняться и случайными отклонениями. Первый случай соответствует изменению параметра распределения Пуассона, а второй — его постоянству. Поэтому обосновать вывод о появлении очага заражения можно, отклонив статистическую гипотезу о равенстве параметров распределений Пуассона, описывающих число заболевших в соседние годы.

Полученные результаты представляли достаточно большой интерес для практической медицины. В частности, был сделан вывод о наличии местной заболеваемости в двух конкретных областях, после чего были обнаружены очаги заболевания описторхозом в этих областях.

Итак, сравнение групп проводят с помощью статистических методов проверки однородности. В научных медицинских исследованиях до сих пор часто применяют критерий Стьюдента для проверки однородности двух выборок. Однако он опирается на два предположения — о нормальном распределении результатов наблюдений и о равенстве дисперсий для двух групп. Ни то, ни другое предположение обычно не выполнено в научных медицинских исследованиях. Поэтому современная прикладная статистика рекомендует вместо критерия Стьюдента применять иные критерии [13, 14], а именно, критерий Крамера-Уэлча [15], непараметрические критерии Вилкоксона [16, 17], Смирнова, Лемана-Розенблатта [18].