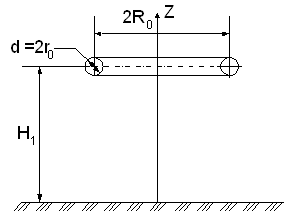
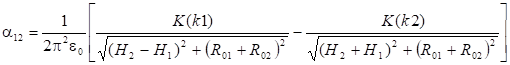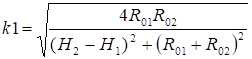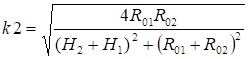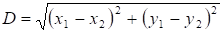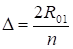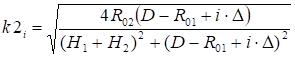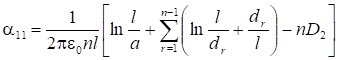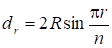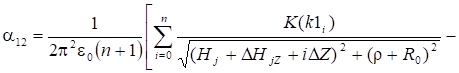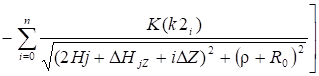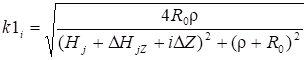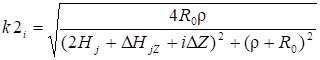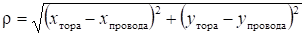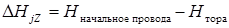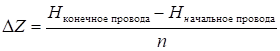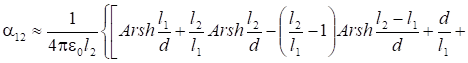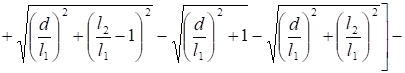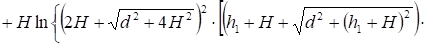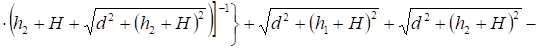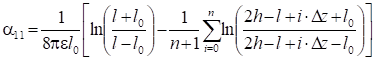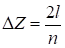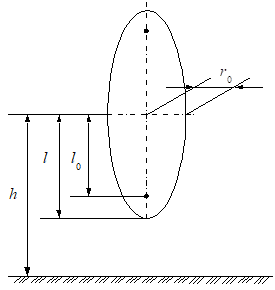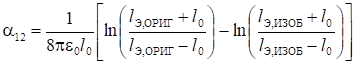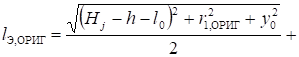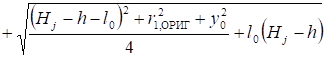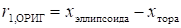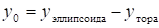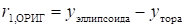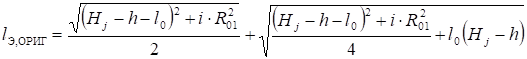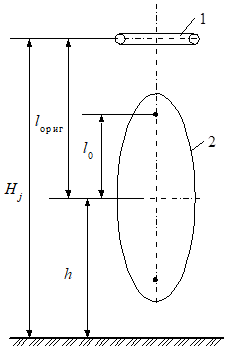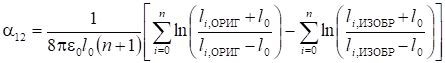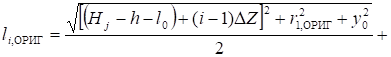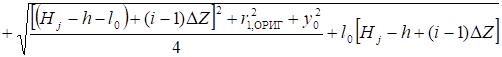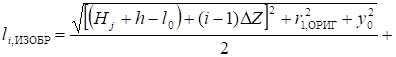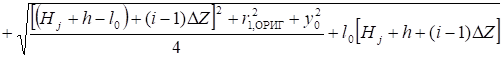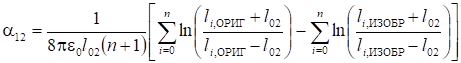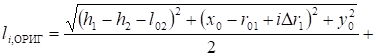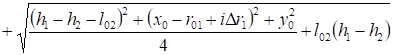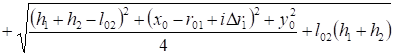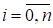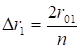Собственный потенциальный коэффициент тороида, осевая линия которого перпендикулярна проводящей плоскости (рис. 4).

(4).
где _ модуль полного эллиптического интеграла первого рода K(k), численные значения которого приведены в таблице 1.
R0 — радиус тороида,.
r0 _ радиус сечения тороида,.
H1 — высота тороида над проводящей плоскостью.
Рисунок 4.
Таблица 1.
|
| K(k). | | K(k). | | K(k). | | K(k). | |
| 1.5708. | | 1.6365. | | 1.8691. | | 2.461. | |
| 1.5709. | | 1.6426. | | 1.8848. | | 2.5046. | |
| 1.5713. | | 1.649. | | 1.9011. | | 2.5507. | |
| 1.5719. | | 1.6557. | | 1.918. | | 2.5998. | |
| 1.5727. | | 1.6627. | | 1.9356. | | 2.6521. | |
| 1.5738. | | 1.6701. | | 1.9539. | | 2.7081. | |
| 1.5751. | | 1.6777. | | 1.9729. | | 2.7681. | |
| 1.5767. | | 1.6858. | | 1.9927. | | 2.8327. | |
| 1.5785. | | 1.6941. | | 2.0133. | | 2.9026. | |
| 1.5805. | | 1.7028. | | 2.0347. | | 2.9786. | |
| 1.5828. | | 1.7119. | | 2.0571. | | 3.0617. | |
| 1.5854. | | 1.7214. | | 2.0804. | | 3.1534. | |
| 1.5882. | | 1.7312. | | 2.1047. | | 3.2553. | |
| 1.5913. | | 1.7415. | | 2.13. | | 3.3699. | |
| 1.5946. | | 1.7522. | | 2.1565. | | 3.5004. | |
| 1.5981. | | 1.7633. | | 2.1842. | | 3.6519. | |
| 1.602. | | 1.7748. | | 2.2132. | | 3.8317. | |
| 1.6061. | | 1.7868. | | 2.2435. | | 4.0528. | |
| 1.6105. | | 1.7992. | | 2.2754. | | 4.3387. | |
| 1.6151. | | 1.8122. | | 2.3088. | | 4.7427. | |
| 1.62. | | 1.8256. | | 2.3439. | | 5.4349. | |
| 1.6252. | | 1.8396. | | 2.3809. | | | |
| 1.6307. | | 1.8541. | | 2.4198. | | | |
|
Примечание:. Для работы с таблицей 1 после вычисления округлить или отбросить дробную часть.

Два коаксиальных тороида (рис. 5).
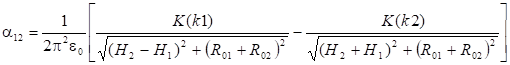
(5).
и ,.
Рисунок 5.
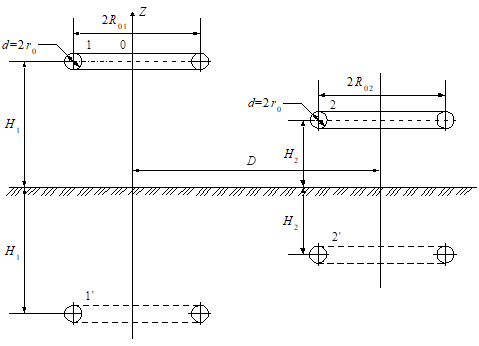
Два нескрещивающихся тороида, осевые линии которых расположены в параллельных горизонтальных плоскостях (рис. 6).

(6).
где D — расстояние между центрами торов ,.
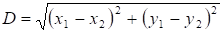
n целое число (принять равным 20),.
и.
Рисунок 6.
Несколько соединенных между собой одинаковых прямолинейных проводов, перпендикулярных проводящей плоскости (рис. 7).
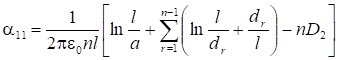
(7).
где (r=1, 2, …, n-1); D2 — коэффициент, определяемый по отношению h/l из таблицы 2.
Таблица 2.
|
h/l | D2 | h/l | D2 | h/l | D2 |
0.02. | 0.928. | 0.30. | 0.645. | 1.11. | 0.465. | |
0.04. | 0.884. | 0.40. | 0.604. | 1.25. | 0.451. | |
0.06. | 0.850. | 0.50. | 0.569. | 2.00. | 0.408. | |
0.08. | 0.820. | 0.60. | 0.554. | 2.50. | 0.392. | |
0.10. | 0.795. | 0.70. | 0.523. | 5.00. | 0.352. | |
0.15. | 0.744. | 0.80. | 0.504. | 10.0. | 0.332. | |
0.20. | 0.702. | 0.90. | 0.489. | | | |
0.25. | 0.670. | 1.00. | 0.477. | | | |
|
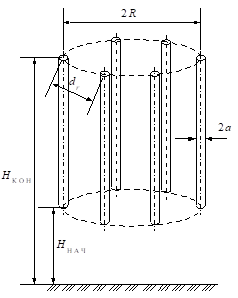
Рисунок 7.
Тороид и провод конечной длины (рис. 8).
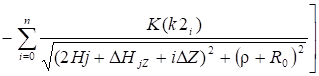
(8).
где ,.
.
_ расстояние между центром тора и проводом.
.
.
.
n целое число (принять равным 20),.
Рисунок 8.
Два провода конечной длины (рис. 9).

(9).
Рисунок 9.
Эллипсоид вращения, одна из осей которого перпендикулярна проводящей плоскости (рис. 10).
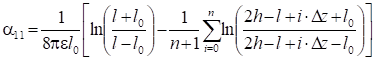
(10).
где l — большая полуось эллипсоида,.
l0 — полуфокусное расстояние,.
h — высота центра эллипсоида;
.
Рисунок 10.
Тороид и проводящее тело в форме эллипсоида вращения (рис. 11).
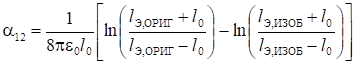
(11).
где lЭ, ОРИГ и lЭ, ИЗОБ — большие полуоси эллипсоидов вращения, являющихся эквипотенциальными поверхностями электростатических полей, создаваемых электродом в форме эллипсоида и его изображением.
Они соответственно равны:
, или.
.
Рисунок 11.
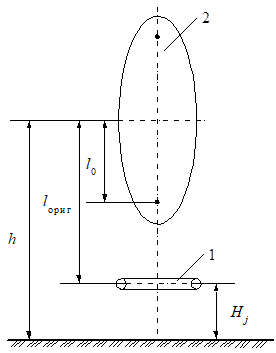
Соосные тороид и эллипсоид вращения (рис. 12).

(12).
.
.
где i=0;1;1.
Рисунок 12.
Эллипсоид вращения и провод конечной длины (рис. 13).
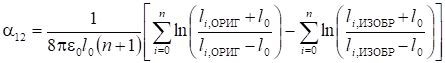
(13).
Рисунок 13.
Два непересекающихся эллипсоида вращения (рис. 14).
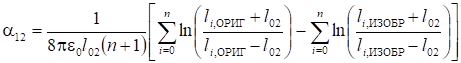
(14).
где и .
Рисунок 14.