Уравнение состояния идеального газа

Состояние заданной массы газа определяется значениями трех параметров: давления p, объема V и температуры T. Эти параметры закономерно связаны друг с другом, так что изменение одного из них влечет за собой изменение других. Указанная связь может быть задана аналитически или в виде функции.

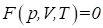
. (1.15).

Соотношение, определяющее связь между параметрами какого-либо тела, называется уравнением состояния этого тела. Следовательно, (1.15) представляет собой уравнение состояния данной массы газа.

Простейшими свойствами обладает воображаемый газ, взаимодействие между молекулами которого пренебрежимо мало. Такой газ называется идеальным. Взаимодействие между молекулами всякого газа становится пренебрежимо слабым при большом разрежении, т. е. при малых плотностях газа. Всякий реальный газ при достаточном разрежении близок по своим свойствам к идеальному. Некоторые газы, такие как воздух, азот, кислород, даже при обычных условиях, т. е. при комнатной температуре и атмосферном давлении, мало отличаются от идеального газа. Особенно близки по своим свойствам к идеальному газу гелий и водород.

При небольших плотностях газы с хорошей точностью подчиняются уравнению.

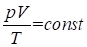
. (1.16).

Следовательно, это уравнение есть уравнение состояния идеального газа.

В соответствии с законом, установленным Авогадро, моли всех газов занимают при одинаковых условиях (т.е. при одинаковых температуре и давлении) одинаковый объем. В частности, при так называемых нормальных условиях, т. е. при 0 °C и при давлении в 1 атм (1,01· 10⁵ Па), объем моля любого газа равен. Отсюда следует, что в случае, когда количество газа равно одному молю, величина константы в (1.16) будет одинакова для всех газов. Обозначив соответствующую молю величину константой R, напишем уравнение (1.16) следующим образом:

. (1.17).

Мы поставили при V индекс «м», чтобы показать, что речь идет об объеме, занимаемом при данных p и T молем газа. Уравнение (1.17) есть уравнение состояния идеального газа, написанное для одного моля.

Величина R называется газовой постоянной. Согласно соотношению (1.17) и закону Авогадро.

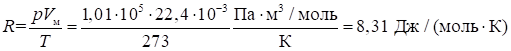
(произносится: джоуль на моль-кельвин) Для практических расчетов иногда бывает удобно пользоваться значением R в литр-атмосферах на моль-кельвин:. .

От уравнения (1.17) для одного моля легко перейти к уравнению для любой массы m, приняв во внимание, что при одинаковых давлениях и температуре н молей газа будут занимать в н раз больший объем, чем один моль:. Умножив (1.17) на (m — масса газа, M — молярная масса) и заменив нV_м на V, получим уравнение.

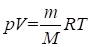
. (1.18).

Это уравнение представляет собой уравнение состояния идеального газа, написанное для массы газа m.

Уравнению (1.18) можно придать другой вид. Для этого введем величину.

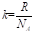
. (1.19).

(R — газовая постоянная, N_A — число Авогадро). Эта величина называется постоянной Больцмана. Она имеет более глубокий физический смысл, чем постоянная R. Далее будет показано, что k представляет собой коэффициент пропорциональности между средней энергией теплового движения молекулы и абсолютной температурой. Подстановка в (1.19) числовых значений R и N_A дает.

.

Умножим и разделим правую часть уравнения (1.18) на N_A. Тогда уравнение можно написать в виде.

.

Произведение нN_A равно числу молекул N, содержащихся в массе газа m. С учетом этого получаем, что.

. (1.20).

Теперь разделим обе части уравнения (1.20) на V. Приняв во внимание, что есть число молекул в единице объема n, приходим к формуле.

. (1.21).

Уравнения (1.18), (1.20) и (1.21) представляют собой различные формы записи уравнения состояния идеального газа.

Отношение массы газа к занимаемому им объему дает плотность газа:. Согласно (1.18) плотность идеального газа.

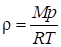
. (1.22).

Таким образом, плотность идеального газа пропорциональна давлению и обратно пропорциональна температуре.

Простая связь между температурой и остальными параметрами идеального газа делает заманчивым использование его в качестве виртуального термометрического вещества. Обеспечив постоянство объема и используя в качестве температурного признака давление газа, можно получить воображаемый термометр с идеально линейной температурной шкалой. В дальнейшем эту шкалу мы будем называть идеальной газовой шкалой температур.

Практически, по международному соглашению, в качестве термометрического тела берется водород. Установленная по водороду с использованием уравнения (1.18) шкала называется эмпирической шкалой температур.