Прямоугольный волновод. 
Прямоугольный волновод

Вывод формул для поля

Прямоугольный волновод представляет собой полую металлическую трубу прямоугольного сечения (рис.7). Предположим, что стенки волновода обладают бесконечной проводимостью, а заполняющая его среда — идеальный диэлектрик с параметрами е и м. В такой направляющей системе могут существовать волны Е и H и не могут существовать ТЕМ-волны. На рис. 7 показаны используемая система координат и размеры, а и b поперечного сечения волновода. Для определенности будем считать, что а? b, а источники, создающие поле, расположены со стороны отрицательных значений переменной z за пределами рассматриваемой части линии передачи (созданная ими волна распространяется в положительном направлении оси Z). При а>Ь стенки с поперечными размерами, а и b будем называть соответственно широкой и узкой стенками прямоугольного волновода.

Так как поперечные составляющие векторов поля выражаются через продольные, то для вычисления поля волн Е и Н достаточно определить составляющую Emz или Нтz соответственно. Составляющие Етz и Hmz удовлетворяют уравнению Гельмгольца.

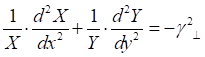
(1).

Рис. 7.

где функция w равна Emz для E-волн и Нтzдля Н-волн, = k2-в2, а в — коэффициент фазы рассматриваемой волны. Правая часть уравнения (1) равна нулю, так как по предположению сторонние источники расположены за пределами рассматриваемой части волновода. Фактически задача состоит в нахождении так называемых собственных волн прямоугольного волновода.

Для решения уравнения (1) применим метод разделения переменных. Запишем функцию w в виде w? w (x, y, z, t) = w0(x, у) exp [I (щt-вz)]. Очевидно, что функция w0(x, y) также удовлетворяет уравнению (1). Представим ее в виде произведения двух функций, каждая из которых зависит только от одной переменной:

w0(x, y) = X (x) Y (y). (2).

Перейдем в (1) к функции w0 (x, у) и подставим (2). После деления обеих частей уравнения на произведение Х (х)У (у) получаем.

(3).

Так как переменные x и у являются независимыми, то левая часть уравнения (3) представляет собой сумму двух независимых функций, а правая равна постоянной. Это возможно только при выполнении соотношений d2X/dx2 + гx2Ч = 0 и d2Y/dy2 + гy2Y = 0, где гx и гy — некоторые, пока неизвестные постоянные, удовлетворяющие равенству гx2+ гy2= (4).

Решая полученные уравнения, находим Х (х) = A sin (гx х) + B cos (гxx),.

У (у) = С sin (гy у) + D cos (гyy).

где А, В, C и D — некоторые, пока также неизвестные, постоянные.

В случае Е-волн (Ez?0, Hz=0) функция w-Emz. Составляющая Eтz является касательной ко всем стенкам волновода. Поэтому должны выполняться следующие краевые условия:

w0 (0, y) = 0, w0 (x, 0) = 0, (6).

w0 (а, у) = 0, w0 (х, b) = 0, (7).

где 0? х?а, 0? у?b. Равенства (6) эквивалентны условиям X (0) = 0 и Y (0) = 0 из которых следует, что B = 0 и D= 0. Из условий (7) вытекают равенства A sin (гx) = 0 и C sin (гy b) = 0. Постоянные, А и С должны быть отличны от нуля, иначе Eтz? 0, что в случае Е-волн невозможно. Поэтому имеют место соотношения.

sin (гxa) = 0 и sin {гyb) = 0. (8).

Из (8) находим значения постоянных гx и гy:

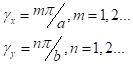
Отметим, что в случае Е-волн значения m = 0иn= 0 не годятся, так как при этом случае Eтz = 0 во всех точках внутри волновода.

Введем обозначение AЧC = E0z и выпишем окончательные выражения для составляющих векторов поля Е-волн в прямоугольном волноводе:

Emv (x, y, z)=E0v (x, y) exp (-iвz), v = x, y, z, (10а).

Hmv (x, y, z) = Hv0(x, y) exp (-iвz), v = x, y,.

где.

E0z (x, у) = E0z sin (m р x/a) sin (n р y/b),.

E0х (х, у) = -i (в /) E0z (m р x/a) cos (m р x/a) sin (n р y/b),.

E0y (x, y) = -i (в /) E0z (m р x/b) sin (m р x/a)cos (n р y/b), (10б).

H0х (х, у) = Я (ще/) E0z (m р x/b) sin (m р x/a)cos (n р y/b),.

H0y (х, у) = -Я (ще/) E0z (m р x/a) cos (m р x/a) sin (n р y/b),.

H0y (х, у) = 0.

Индекс m в формулах (10а) и (10б) имеет совершенно разный смысл. В (10а) он указывает, что рассматриваются комплексные амплитуды составляющих векторов поля, а в (10б) индекс т — натуральное число, определяющее значение постоянной гx1 как это следует из формулы (10.9).

Значение постоянной находится из формул (4) и (9):

(11).

Зная, определяем критическую длину волны:

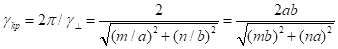
(12).

Коэффициент фазы в вычисляется по известной формуле.

Перейдем к анализу свойств поля E-волн, описываемого выражениями (10), выведем формулы для поля H-волн в прямоугольном волноводе. Волны E и H имеют много общих черт, и их свойства удобно анализировать совместно.

В случае H-волн (Hz? 0, Ez=0) функция w=Hmz. Решение уравнения (1) строится так же, как для Е-волн. Изменяются только краевые условия. Требуя, чтобы касательные составляющие вектора E на стенках волновода обращались в нуль, имеем.

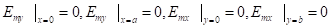
(13).

Но искомой является функция w, поэтому выписанные краевые условия следует преобразовать в условия для функции w. Поперечные составляющие вектора Eт выражаются через Hmz. Из этого соотношения и краевых условий (13) после перехода к функции w0(x, у) получаем.

(14).

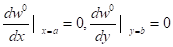
(15).

Равенства (14) эквивалентны условиям Х'(0) = 0 и Y' (0) = 0, из которых следует, что, A=C=0, т. е. Х (х)-В cos (гxx) и Y (у) = D cos (гуу). Так как B?0 и D?0 (в противном случае Hz? 0), то из соотношений (15) вытекают уравнения (.8). Следовательно, гx=mр/а, m = 0,1,2… гx=nр/b, n = 0,1,2… (16).

В отличие от (9) в случае H-волн индексы m и n могут принимать нулевые значения. Однако они не могут равняться нулю одновременно: при этом составляющая Hz не зависит от переменных x и у и вектор E будет тождественно равен нулю, что невозможно. Выпишем окончательные выражения для комплексных амплитуд составляющих векторов поля Нволн в прямоугольном волноводе:

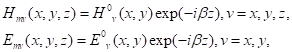
H0z (х, у) = H0z cos (m р x/a) cos (n р y/b), (17а).

H0х (х, у) = i (в /) (m р /a) H0z sin (m р x/a) cos (n р y/b), (17б).

H0y (х, у) = i (в /) (n р /b) H0z cos (m р x/a) sin (n р y/b),.

E0х (х, у) = Я (ще/) (n р x/b) H0z cos (m р x/a) sin (n р y/b),.

E0х (х, у) = -Я (ще/) (m р x/a) H0z sin (m р x/a) cos (n р y/b),.

E0z (х, у) = 0.

Аналогично случаю Е-волн в формулах (17а) индекс m указывает, что рассматриваются комплексные амплитуды составляющих векторов поля, а в формулах (17б) n связано с постоянной гx соотношением (16).

Составляющие векторов поля З-волн найдены с точностью до произвольного постоянного множителя H0z, определение которого в рамках выбранной электродинамической модели невозможно (см. аналогичное замечание, сделанное при анализе Е-волн).

Легко показать, что поперечное волновое число гx и критическая длина волны лкр в случае З-волн также определяются формулами (11) и (12) соответственно.

Перейдем к анализу свойств Eи З-волн в прямоугольном волноводе. Как видно из формул (10) и (17), в прямоугольном волноводе возможно существование различных Eи Н-волн, структура поля которых зависит от значений индексов тип. Каждая пара значений индексов тип определяет свои волны, которые обозначают Еmn (в случае Е-волн) или Нmn (в случае Н-волн). При этом у Е-волн m? 1 и n? 1, а у З-волн один из индексов может равняться нулю.

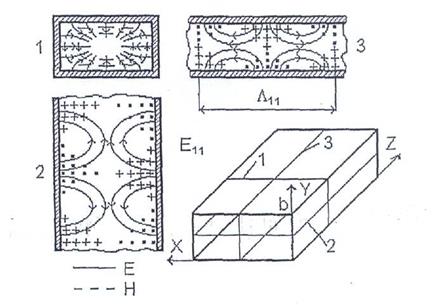
Рис. 8.

Структура поля в поперечном сечении (при фиксированном значении координаты z) аналогична структуре стоячей волны, и ее можно характеризовать длинами волн лx = 2а/т и лy =2b/п в направлениях осей X и У соответственно. Индекс m, таким образом, равен числу полуволн (лx/2), укладывающихся на поперечном размере, а стенки, параллельной оси X. Аналогично индекс n равен числу полуволн (лy/2), укладывающихся на поперечном размере b стенки, параллельной оси Y. Равенство нулю одного из индексов означает, что поле рассматриваемой волны не зависит от соответствующей координаты (при m = 0 — от координаты х, а при n = 0 — от координаты у).

Изменение всех составляющих комплексных амплитуд векторов E и З вдоль оси Ж описывается множителем exp (-iЯz). Распространение волны происходит только при л <�лкр (предполагается. что в волноводе отсутствуют потери энергии). Критическая длина волны вычисляется по формуле (12). Она зависит от размеров, а и b и от индексов m и n. При увеличении значений индексов m и n и фиксированных размерах, а и b значение лкр уменьшается. Наибольшую лкс среди всех возможных волн при а> b имеет волна Н10. Соответствующая ей лкс равна 2а. При, а = b наибольшую лкр имеют две волны Н10 и Н01. Волну, имеющую наибольшую лкр, называют основной волной рассматриваемой линии передачи (или волной низшего типа). Таким образом, при а>Ь основной волной прямоугольного волновода является волна Н10.

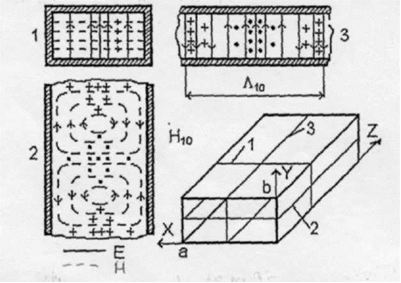
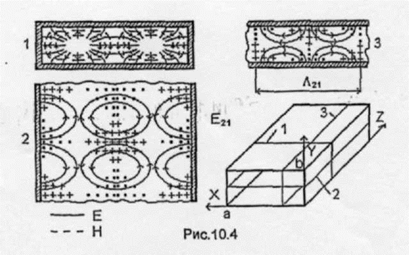
Рис. 9.

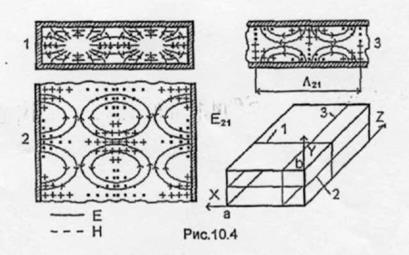
Рис. 10.

Отметим, что, зная структуру поля волны E11, легко построить структуру поля волны Еmn при любых значениях индексов m и n. Например, структура поля волны Е21 представляет собой объединение структур двух волн Е11 (рис. 8). Для построения структуры волны Еmn нужно мысленно разделить волновод на mn «волноводных секций». Структура поля в каждой секции будет соответствовать структуре поля волны Е11 а линии векторов будут непрерывно переходить из одной «секции» в другую. Аналогично волну Н20 можно представить как бы состоящей из двух волн Н10.

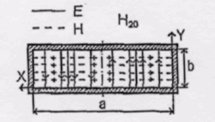
Рис. 11.

Структура поля волны Н20 в поперечном сечении показана на рис. 11.

При л>лкр волна не распространяется: образуется стоячая волна, амплитуды составляющих векторов Е и З которой экспоненциально убывают вдоль оси Z (в этом случае Я= -i|Я| и exp (-iЯz) = exp (-|Я|z). Напомним, что анализ проводится в предположении отсутствия потерь.