Типичные примеры анализа моделей

При анализе статистических зависимостей широко используются графические методы, которые задают направление его дальнейшего анализа. В Excel для этого можно использовать средство Мастер диаграмм. Для создания диаграммы необходимо выделить данные, запустить мастер диаграмм, выбрать тип и вид диаграммы (для нашего примера тип диаграммы — Точечная), выбрать и уточнить ориентацию диапазона данных… Читать ещё >
Типичные примеры анализа моделей (реферат, курсовая, диплом, контрольная)
Задача 1.
Торговое предприятие имеет сеть, состоящую из 12 магазинов, информация о деятельности которых представлена следующими данным (табл. 3).
Таблица 3
№ магазина. | Среднее число посетителей в день, тыс. чел, х | Годовой товарооборот, млн руб., у | № магазина. | Среднее число посетителей в день, тыс. чел, х | Годовой товарооборот, млн руб., у | |
8,25. | 19,76. | 12,36. | 75,01. | |||
10,24. | 38,09. | 10,81. | 89,05. | |||
9,31. | 40,95. | 9,89. | 91,13. | |||
11,01. | 41,08. | 13,72. | 91,26. | |||
8,54. | 56,29. | 12,27. | 99,84. | |||
7,51. | 68,51. | 13,92. | 108,55. |
Задания:
- 1. Построить линейную модель y = b0 + b1x, параметры которой оценить методом наименьших квадратов.
- 2. Оценить тесноту и направление связи между переменными с помощью коэффициента корреляции, найти коэффициент детерминации и пояснить его смысл.
- 3. Проверить значимость уравнения регрессии на 5%-м уровне по F-критерию, проверить значимость коэффициента регрессии по t-статистике.
Решение:
При анализе статистических зависимостей широко используются графические методы, которые задают направление его дальнейшего анализа. В Excel для этого можно использовать средство Мастер диаграмм. Для создания диаграммы необходимо выделить данные, запустить мастер диаграмм, выбрать тип и вид диаграммы (для нашего примера тип диаграммы — Точечная), выбрать и уточнить ориентацию диапазона данных и ряда, настроить параметры диаграммы.
Для описания закономерностей в исследуемой выборке наблюдений строится линия тренда.
Для добавления линии тренда в диаграмму необходимо выполнить следующие действия:
- 1) щелкнуть правой кнопкой мыши по ряду данных;
- 2) в динамическом меню выбрать команду Добавить линию тренда. На экране появится окно Линия тренда (рис. 2);
- 3) выбрать вид зависимости регрессии. Для нашего примера тип тренда определим, как Линейный;
- 4) перейти на вкладку Параметры. В поле Показать уравнение на диаграмме установить подтверждение;
- 5) в случае необходимости можно задать остальные параметры.
Изобразим полученную зависимость графически точками координатной плоскости (рис. 2). Такое изображение статистической зависимости называется полем корреляции.
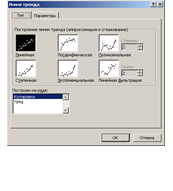
Рис. 2. Диалоговое окно для выбора типа тренда
По расположению эмпирических точек можно предполагать наличие линейной корреляционной (регрессионной) зависимости между переменными х и у.
По данным табл. 2 найдем уравнение регрессии у по х. Расчеты произведем в Excel по формулам (4) — (10), промежуточные вычисления представим в табл. 4.
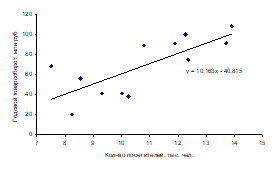
Рис. 3. Поле корреляции
Таблица 4
N. | X. | Y. | X*Y. | X*X. | Y*Y. | |
8,25. | 19,76. | 163,02. | 68,0625. | 390,4576. | ||
10,24. | 38,09. | 390,0416. | 104,8576. | 1450,848. | ||
9,31. | 40,95. | 381,2445. | 86,6761. | 1676,903. | ||
10,01. | 41,08. | 411,2108. | 100,2001. | 1687,566. | ||
8,54. | 56,29. | 480,7166. | 72,9316. | 3168,564. | ||
7,51. | 68,51. | 514,5101. | 56,4001. | 4693,62. | ||
12,36. | 75,01. | 927,1236. | 152,7696. | 5626,5. | ||
10,81. | 89,05. | 962,6305. | 116,8561. | 7929,903. | ||
11,89. | 91,13. | 1083,536. | 141,3721. | 8304,677. | ||
13,72. | 91,26. | 1252,087. | 188,2384. | 8328,388. | ||
12,27. | 99,84. | 1225,037. | 150,5529. | 9968,026. | ||
13,92. | 108,55. | 1511,016. | 193,7664. | 11 783,1. | ||
Сумма. | 128,83. | 819,52. | 9302,173. | 1432,684. | 65 008,55. | |
Среднее. | 10,73 583 333. | 68,2933. | 775,1811. | 119,3903. | 5417,38. | |
Дисперсия. | 4,132 174 306. | 753,4 001 222. | b1. | 10,163. | ||
Cov (x, y). | 41,99 527 222. | b0. | — 40,8149. | |||
Итак, уравнение регрессии у по х:
= 40,81 + 10,16x.
Из полученного уравнения регрессии следует, что при увеличении среднего числа посетителей на 1 тыс. чел. годовой товарооборот увеличивается в среднем на 10,16 млн руб.
По исходным данным вычислим коэффициент корреляции.
Расчеты произведем в Excel, промежуточные вычисления см. табл. 4 и формулы (11), (12).
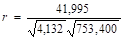
= 0,753,.
т.е. связь между переменными достаточно тесная.
Оценим на уровне значимости = 0,05 значимость уравнения регрессии у по х.
1-й способ. Используя данные табл. 5 вычислим необходимые суммы по формулам табл. 1:
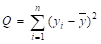
= 9040,801 (см. столбец 6);
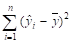
QR = = 5121,574 (см. столбец 7);
Qe = Q QR = 9040,801 — 5121,574 = 3919,228.
По формуле (19).
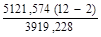
F = = 13,07.
По статистическим таблицам F-распределения F0,05;1;10 = 4,96. Так как F > F0,05;1;26, то уравнение регрессии значимо.
Таблица 5
N. | X. | Y. | Yрег. | Yi-Yрег. | (Yi-Yср)^2. | (Yрег-Yср)^2. | (Xi-Xcp)^2. | |
8,25. | 19,76. | 43,03. | — 23,2698. | 2355,484. | 638,2452. | 6,179 367. | ||
10,24. | 38,09. | 63,254. | — 25,1642. | 912,2413. | 25,39 306. | 0,245 851. | ||
9,31. | 40,95. | 53,802. | — 12,8526. | 747,6579. | 209,9815. | 2,33 001. | ||
10,01. | 41,08. | 60,916. | — 19,8367. | 740,5655. | 54,41 484. | 0,526 834. | ||
8,54. | 56,29. | 45,977. | 10,3129. | 144,08. | 498,0148. | 4,821 684. | ||
7,51. | 68,51. | 35,509. | 33,0008. | 0,46 944. | 1074,799. | 10,406. | ||
12,36. | 75,01. | 84,799. | — 9,7897. | 45,11 361. | 272,4612. | 2,637 917. | ||
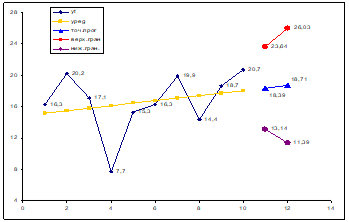 10,81. | 89,05. | 69,047. | 20,0029. | 430,8392. | 0,568 147. | 0,5 501. | ||
11,89. | 91,13. | 80,023. | 11,1069. | 521,5133. | 137,588. | 1,332 101. | ||
13,72. | 91,26. | 98,621. | — 7,3614. | 527,4678. | 919,7921. | 8,905 251. | ||
12,27. | 99,84. | 83,886. | 15,9549. | 995,1922. | 243,102. | 2,353 667. | ||
13,92. | 108,55. | 100,654. | 7,8960. | 1620,599. | 1047,213. | 10,13 892. | ||
Сумма. | 128,83. | 819,52. | 0,00. | 9040,801 | 5121,574 | 49,58 609. | ||
Среднее. | 10,736. | 68,293. | ||||||
b1. | 10,163. | |||||||
b0. | — 40,8149. |
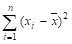
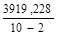
2-й способ. Учитывая, что b1 = 10,163, = 49,586 (табл. 4), = =391,92 (табл. 1), по формуле (20).
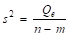
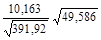
t = = 3,61.
По таблице t-распределения t0,95;10 = 2,23. Так как t > t0,95;26, то коэффициент регрессии b1, а значит, и уравнение парной линейной регрессии значимо.
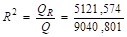
Найдем коэффициент детерминации и поясним его смысл. Ранее было получено QR = 5121,574, Q = 9040,801. По формуле (22) = 0,5665 (или R2 = r2 = 0,7532 = 0,95 665). Это означает, что изменения зависимой переменной у — годовой товарооборот …
lnу = 2,5 + 0,2lnx + e, r2 = 0,68.
(6,19)
у = 1,1 + 0,8lnх + е, r2 = 0,69.
(6,2)
у = 3 + 1,5х + 0,1х2 + е,r2 = 0,701.
(3,0)(2,65)
В скобках указаны фактические значения t-критерия.
Задания:
- 1. Определите коэффициент детерминации для 1-го уравнения.
- 2. Запишите функцию, характеризующую зависимость у от х во 2-м уравнении.
- 3. Определите коэффициенты эластичности для каждого из уравнений для х0 = 2,5 тыс. шт.
Решение:
1. Чтобы определить коэффициент детерминации воспользуемся формулой (21).
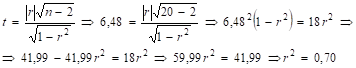
Для уравнения парной линейной регрессии коэффициент детерминации r2 = 0,70.
2. Уравнение 2 — это степенная функция, к которой применили преобразование. В качестве преобразования выполнили логарифмирование. Чтобы записать функцию проведем обратные преобразования.
lnу = 2,5 + 0,2lnx + e у = е2,5 • х0,2 у = 1,28х0,2.
3. Чтобы рассчитать коэффициенты эластичности воспользуемся данными табл. 2. Результаты расчетов объединим в табл. 6.
Таблица 6
Вид функции. | Коэффициент эластичности. | |
Линейная. у = 3 + 2х + е | ||
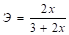 Парабола. у = 3 + 1,5х + 0,1х2 + е | ||
Степенная. у = 1,28х0,2 | Э = 1,28. | |
Полулогарифмическая у = 1,1 + 0,8lnx | ||
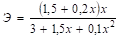
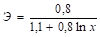
Рассчитаем точечный коэффициент эластичности для значения х0 = 2,5.
1. Для линейной модели у = 3 + 2х + е.
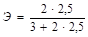
= 0,625.
2. Для параболы у = 3 + 1,5х + 0,1×2 + е.
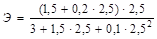
= 0,678.
3. Для степенной функции у = 1,28×0,2.
Э = 1,28.
4. Для полулогарифмической функции у = 1,1 + 0,8lnx.
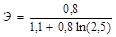
= 0,436.
Задача 3.
По совокупности 30 предприятий торговли изучается линейная зависимость между ценой товара А (тыс. руб.) х и прибылью торгового предприятия (млн ру6.) у.
При оценке регрессионной модели были получены следующие промежуточные результаты:
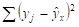
= 39 000,.
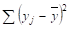
= 120 000.
Задания:
- 1. Поясните, какой показатель корреляции можно определить по вышеприведенным данным:
- 2. Постройте таблицу дисперсионного анализа для расчета значения F-критерия Фишера.
- 3. Сравните фактическое значение F-критерия с табличным. Сделайте выводы.
Решение:
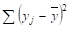
1. Оценим исходные данные задачи. Величина называется остаточная сумма квадратов (Qe), а полная сумма квадратов (Q). Исходя из условия задачи, можно рассчитать коэффициент детерминации по формуле (22), а затем индекс корреляции. Тогда,.
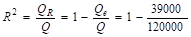
= 0,675.
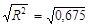
R = = 0,822.
2. Для дисперсионного анализа воспользуемся табл. 1 и формулами (17), (18). Результаты расчетов приведем в табл. 7.
Таблица 7
Компоненты дисперсии. | Сумма квадратов. | Число степеней свободы. | Дисперсия на одну степень свободы. | Fфакт | |
Объясненная. | QR = 81 000. | m — 1 = 1. | 58,15. | ||
Остаточная. | Qe = 39 000. | n — m = 28. | 1392,86. | ||
Общая. | Q = 120 000. | n — 1 = 29. | |||
3. По статистическим таблица представленным в приложении найдем F0,05;1;28 = 4,20. Так как наблюдаемое значение статистики Фишера Fфакт больше табличного (Fфакт > F0,05;1;28), то полученная модель является адекватной.
Задача 4.
По 28 предприятиям концерна изучается зависимость дневной выработки (ед.) у от уровня механизации труда (%) х по следующим данным (табл. 8).
Таблица 8
i | x | y | i | x | y | i | x | y | |
Задания:
- 1. Проверьте гипотезу об отсутствии гетероскедастичности в линейной регрессии с помощью теста ранговой корреляции Спирмэна при вероятности 0,95.
- 2. С помощью теста Гольдфельда-Квандта исследуйте гетероскедастичность остатков.
Решение:
Тест ранговой корреляции Спирмэна
Проранжируем значения хi и абсолютные величины остатков в порядке возрастания, расчеты занесем в табл. 9.
Найдем коэффициент ранговой корреляции Спирмэна:
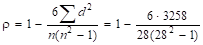
= 0,108.
Таблица 9
N. | X. | Ei. | Расчет ранговой корреляции. | ||||
Ранг Х. | Ранг |Ei|. | d. | d2. | ||||
13,27. | — 27. | ||||||
7,61. | — 24. | ||||||
— 5,71. | — 20. | ||||||
— 5,67. | — 18. | ||||||
— 1,15. | — 1. | ||||||
— 2,15. | — 3. | ||||||
— 0,63. | |||||||
— 2,11. | |||||||
2,15. | — 1. | ||||||
0,41. | |||||||
0,67. | |||||||
— 2,03. | |||||||
— 2,77. | |||||||
— 2,51. | |||||||
— 3,25. | — 2. | ||||||
— 2,99. | |||||||
— 4,47. | — 2. | ||||||
— 5,43. | — 2. | ||||||
— 2,91. | |||||||
— 3,13. | |||||||
— 3,87. | |||||||
2,17. | |||||||
— 0,31. | |||||||
— 1,01. | |||||||
5,77. | |||||||
5,55. | |||||||
6,07. | |||||||
8,11. | |||||||
Сумма. | 0,00. | ||||||
Найдем t-критерий для ранговой корреляции:
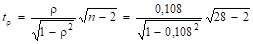
= 0,556.
Сравним полученное значение t с табличным значением t0,95; 26 = 2,06. Так как t < t0,95; 26, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.
Тест ГолфредаКвандта
Упорядочим п наблюдений по мере возрастания переменной х. Исключим из рассмотрения С = 6 центральных наблюдений (условие (п С)/2 = (28 — 6)/2 = 11 > р = 1 выполняется). Разделим совокупность из (п С) = (28 — 6) = 22 наблюдений на две группы (соответственно с малыми и большими значениями фактора х по 11 наблюдений) и определим по каждой из групп уравнения регрессии. Для первой группы оно составит = 3,70 + 0,39x. Для второй группы: = 1,16 + 53,11x. Определим остаточные суммы квадратов для первой (S1) и второй (S2) групп. Промежуточные расчеты занесем в табл. 10.
Таблица 10
N. | X. | Y. | Yрег = -3,70 + 0,39Х. | e=Y-Yрег. | e2. | |
2,15. | 2,85. | 8,1225. | ||||
5,66. | 0,34. | 0,1156. | ||||
12,68. | — 6,68. | 44,6224. | ||||
14,24. | — 5,24. | 27,4576. | ||||
15,02. | — 0,02. | 0,0004. | ||||
15,02. | — 1,02. | 1,0404. | ||||
15,8. | 1,2. | 1,44. | ||||
16,58. | 0,42. | 0,1764. | ||||
16,97. | 5,03. | 25,3009. | ||||
17,36. | 3,64. | 13,2496. | ||||
S1. | 121,5258. | |||||
N. | X. | Y. | Yрег = -53,11 + 1,16Х. | e=Y-Yрег. | e2. | |
23,45. | 1,55. | 2,4025. | ||||
28,09. | — 1,09. | 1,1881. | ||||
30,41. | 0,59. | 0,3481. | ||||
33,89. | — 0,89. | 0,7921. | ||||
35,05. | — 2,05. | 4,2025. | ||||
39,69. | 2,31. | 5,3361. | ||||
42,01. | — 1,01. | 1,0201. | ||||
47,81. | — 3,81. | 14,5161. | ||||
51,29. | 1,71. | 2,9241. | ||||
54,77. | 0,23. | 0,0529. | ||||
57,09. | — 0,09. | 0,0081. | ||||
61,73. | 0,27. | 0,0729. | ||||
S2. | 32,8636. | |||||
Найдем отношение R = S1/S2, где S1 > S2.
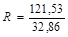
= 3,69.
Сравним эту величину с табличным значением F-критерия с числом степеней свободы 8 для каждой остаточной суммы квадратов F0,05;8;8 = 3,44. Так как R > F0,05;8,8, делаем вывод о наличие гетероскедастичности остатков.
Задача 5.
Имеются данные среднегодовой стоимости основных фондов, (млн руб.) х1, среднегодовой стоимости оборотных средств (млн руб.) х2 и величины валового дохода за год (млн руб.) у по 25 предприятиям, которые представлены в табл. 11.
Таблица 11
i | у | х1 | х2 | |
Задания:
- 1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров.
- 2. Рассчитать частные коэффициенты эластичности, а также стандартизированные коэффициенты регрессии; сделать вывод о силе связи результата и фактора.
- 3. Рассчитать парные, частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы.
- 4. Проверить значимость уравнения регрессии на 5%-м уровне по F-критерию, проверить значимость коэффициентов регрессии по t-статистике.
Решение:
1. По данным табл. 11 найдем уравнение регрессии у по х1, х2. Расчеты произведем в Excel по формуле (32), промежуточные вычисления представим в табл. 12.
Система уравнений для расчета коэффициентов регрессии примет вид:
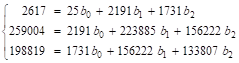
Таблица 12.
i | х1 | х2 | у | yх1 | yх2 | х1^2. | х2^2. | x1x2 | у^2. | |
Сумма. | ||||||||||
Решив систему уравнений методом Гаусса, получили следующие значения коэффициентов регрессии b0 = 34,121; b1 = 0,788; b2 = 1,008.
Уравнение множественной линейной регрессии примет вид:
у = 34,121 + 0,788х1 + 1,008х2.
Коэффициент регрессии b1 показывает, что при увеличении на 1 млн руб. среднегодовой стоимости основных фондов (х1) валовой доход (у) в среднем увеличится на 0,788 млн руб. при постоянном значении среднегодовой стоимости оборотных средств (х2). Если же увеличится среднегодовая стоимость оборотных средств (х2) на 1 млн руб., а стоимость основных фондов (х1) в среднем не изменится, то валовой доход (у) увеличится в среднем на 1,008 млн руб.
2. Рассчитаем коэффициенты и Ej для рассматриваемого примера по формуле (33).
Предварительно найдем значения среднеквадратичного отклонения для переменных задачи, используя данные табл. 12.
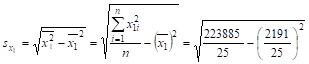
= 35,702;
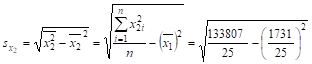
= 23,624;
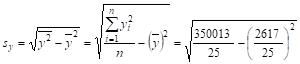
= 55,160.
Тогда,.
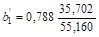
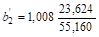
= 0,510= 0,432.
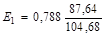
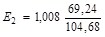
= 0,659= 0,667.
С увеличением среднегодовой стоимости основных фондов на 1% от среднего уровня годовой валовой доход возрастет на 65,9% от своего среднего уровня при фиксированном значении среднегодовой стоимости оборотных средств. С увеличением стоимости оборотных средств на 1% от среднего уровня годовой валовой доход возрастет на 66,7% от своего среднего уровня при фиксированном значении стоимости основных фондов. Сила влияния стоимости оборотных средств (х2) на доход несколько больше, чем сила влияния стоимости основных фондов (х1).
3. Определим парные коэффициенты корреляции, используя формулу (12) и данные табл. 12.
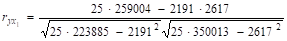
= 0,602;
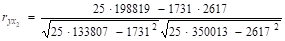
= 0,540;
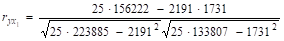
= 0,214.
Парный коэффициент между доходом (у) и стоимостью основных средств (х1) равен 0,602. Парный коэффициент между доходом (у) и стоимостью оборотных средств (х2) равен 0,540. Связь между переменными довольно тесная.
Рассчитаем частные коэффициенты корреляции:
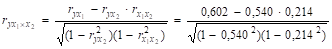
= 0,591;
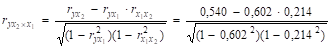
= 0,527.
При сравнении коэффициентов парной и частной корреляции приходим к выводу, что из-за слабой зависимости между факторами (rx1x2 = 0,214 — отсутствие мультиколлинеарности) коэффициенты парной и частной корреляции отличаются незначительно.
Рассчитаем коэффициент множественной корреляции по формуле.
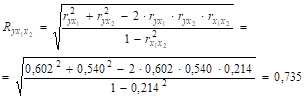
Коэффициент множественной корреляции больше значений парных коэффициентов корреляции. Совокупность факторов оказывает большее совместное влияние на результативный признак.
Для линейных моделей коэффициент множественной детерминации равен квадрату коэффициента множественной корреляции, тогда R2 = 0,7352 = 0,54.
4. Для оценки адекватность уравнения регрессии воспользуемся критерием Фишера. Для расчета Fнабл воспользуемся формулой.
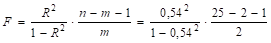
= 12,92.
По таблицам F-критерия прил. 1 F0,05;2;22 = 3,44. Так как F > F0,05;2;17, то уравнение регрессии значимо.
Чтобы оценить значимость параметров регрессии b1 и b2 необходимо найти значения t-статистики. Используя предыдущие расчеты, найдем частные F-критерии Фишера.
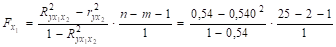
= 12,394;
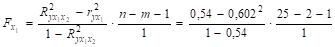
= 8,881.
Для линейных моделей частный F-критерий Фишера связан с t-критерием Стьюдента следующим соотношением:
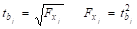
.
Выполнив расчеты, получим.
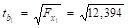
= 3,521;
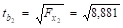
= 2,980.
По таблицам t-распределения прил. 1 t0,95;22 = 2,07. Тогда,.
t1 = 3,521 > t0,95;47 = 2,07 — параметр b1 адекватен;
t2 = 2,980 > t0,95;47 = 2,07 — параметр b2 адекватен.
Задача 6.
Имеются следующие результаты регрессионного анализа зависимости объема выпуска продукции (млн руб.) у от численности занятых на предприятии (чел.) х1 и среднегодовой стоимости основных фондов (млн руб.) х2 по 20 предприятиям отрасли:
Коэффициент детерминации0,81.
Множественный коэффициент корреляции???
Уравнение регрессии ln y = ??? + 0,48 lnx1 + 0,62 lnx2
Стандартные ошибки параметров20,06???
t-критерий для параметров1,5???5.
Задания:
- 1. Напишите уравнение регрессии, характеризующее зависимость у от х1 и х2.
- 2. Восстановите пропущенные характеристики.
- 3. Оцените адекватность полученной модели.
Решение:
1. Для данного уравнения примели преобразование, которое приводит модель нелинейную относительно оцениваемых параметров, к линейной модели: .
Чтобы написать уравнение регрессии сначала восстановим значение параметра а. Воспользуемся формулой (20), в которой отношение обозначим через стандартную ошибку параметра. Тогда.
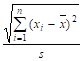
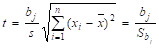
. (39).
Значение параметра а = b0 будет равно а = b0 = t • Sbj = 2 • 1,5 = 3.
Уравнение будет записано в виде: ln y = 3 + 0,48 lnx1 + 0,62 lnx2.
Проведем обратные преобразования и получим уравнение: .
2. Чтобы восстановить пропущенные значение стандартной ошибки коэффициента регрессии и t-критерия также воспользуемся формулой (38).
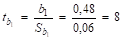
;
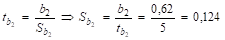
.
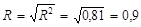
Так как коэффициент детерминации R2 в линейных моделях равен квадрату множественного коэффициента корреляции R, то .
Запишем исходные данные с восстановленными характеристиками:
Коэффициент детерминации0,81.
Множественный коэффициент корреляции0,9.
Уравнение регрессии Стандартные ошибки параметров20,060,124.
t-критерий для параметров1,585.
3. Для оценки адекватность параметров регрессии воспользуемся значениями tнабл. По таблицам t-распределения прил. 1 t0,95;17 = 2,11. Тогда, t1 = 8 > t0,95;17 = 2,11 — параметр b1 адекватен; t2 = 5 > t0,95;17 = 2,11 — параметр b2 адекватен.
Для оценки адекватность уравнения регрессии воспользуемся критерием Фишера. Для расчета Fнабл воспользуемся формулой.
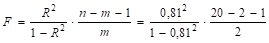
= 16,22.
По таблицам F-критерия прил. 1 F0,05;2;17 = 3,59. Так как F > F0,05;2;17, то уравнение регрессии значимо.
Задача 7.
При изучении уровня потребления мяса (кг на душу населения) у в зависимости от дохода (руб. на одного члена семьи) х1 и в соотношении с уровнем потребления рыбы (кг на душу населения) х2 результаты оказались следующими (по 50 семьям):
Уравнение регрессии = 180 + 0,2х1 0,4х2
Стандартные ошибки параметров20 0,01 0,25.
Множественный коэффициент корреляции0,85.
Задания:
- 1. Используя t-критерий Стьюдента, оцените значимость параметров уравнения.
- 2. Рассчитайте F-критерий Фишера.
- 3. Оцените по частным F-критериям Фишера целесообразность включения в модель:
- а) фактора х1 после фактора х2;
- б) фактора х2 после фактора х1.
Решение:
1. Чтобы найти t-критерий Стьюдента воспользуемся формулой (38).
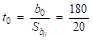
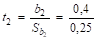
= 9; = 20 = 1,6.
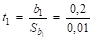
Для оценки адекватность параметров регрессии воспользуемся значениями tнабл. По таблицам t-распределения прил. 1 t0,95;47 = 2,01. Тогда,.
t0 = 9 > t0,95;47 = 2,01 — параметр b0 адекватен;
t1 = 20 > t0,95;47 = 2,01 — параметр b1 адекватен;
t2 = 1,6 < t0,95;47 = 2,01 — параметр b2 неадекватен.
2. Коэффициент детерминации R2 в линейных моделях равен квадрату множественного коэффициента корреляции R.
Отсюда R2 = 0,852 = 0,72.
Для оценки адекватность уравнения регрессии воспользуемся критерием Фишера. Для расчета Fнабл воспользуемся формулой.
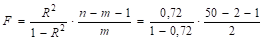
= 21,86.
По таблицам F-критерия прил. 1 F0,05;2;47 = 3,21. Так как F > F0,05;2;47, то в целом уравнение регрессии значимо.
3. Чтобы оценить целесообразность включения в модель дополнительных переменных, необходимо найти частный F-критерий Фишера. Для линейных моделей частный F-критерий Фишера связан с t-критерием Стьюдента следующим соотношением:
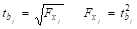
.
Для целесообразности включения фактора х1 после фактора х2 рассчитаем Fx1:
= 202 = 400.
Так как F = 400 > F0,05;2;47 = 3,21, то включение в модель фактора х1 после фактора х2 статистически оправдано.
Для целесообразности включения фактора х2 после фактора х1 рассчитаем Fx2:
= 1,62 = 2,56.
Так как F = 2,56 < F0,05;2;47 = 3,21, то включение в модель фактора х2 после фактора х1 статистически не оправдано.
Задача 8.
Пусть имеются следующие данные об урожайности озимой пшеницы yt (ц/га) за 10 лет (табл. 13):
Таблица 13
t. | |||||||||||
yt | 16,3. | 20,2. | 17,1. | 7,7. | 15,3. | 16,3. | 19,9. | 14,4. | 18,7. | 20,7. |
Задания:
- 1. Построить линейную модель Y(t) = a0 + a1t, параметры которой оценить методом наименьших квадратов (МНК).
- 2. Оценить адекватность построенной модели на основе исследования:
случайной остаточной компоненты по критерию пиков;
независимости уровней ряда остатков по d-критерию (dн = 1,08 и dв = 1,36) и по первому коэффициенту автокорреляции (r = 0,36);
нормальности распределения остаточной компоненты по RS-критерию (критические уровни 2,67 — 3,69).
- 3. Построить точечный и интервальный прогнозы на два шага вперед (t = 1,12 для уровня вероятности 70% и n = 10).
- 4. Отобразить на графике фактические данные, результаты расчетов и прогнозирования.
Решение:
1. Расчеты коэффициентов модели будем проводить по формулам кривых роста оцененных МНК:
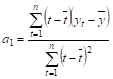
(40).
a0 = a1,(41).
где, средние значения уровней ряда и моментов наблюдения соответственно.
Промежуточные расчеты приведены в табл. 14.
Оценка параметров регрессии:
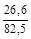
а1 = 0,3224;
а0 = 16,66 — 0,3224 5,5 14,8867.
Таблица 14
t. | yt. | (t-tcp). | (t-tcp)^2. | (y-ycp). | (t-tcp)*(y-ycp). | ||
16,3. | — 4,5. | 20,25. | — 0,36. | 1,62. | |||
20,2. | — 3,5. | 12,25. | 3,54. | — 12,39. | |||
17,1. | — 2,5. | 6,25. | 0,44. | — 1,1. | |||
7,7. | — 1,5. | 2,25. | — 8,96. | 13,44. | |||
15,3. | — 0,5. | 0,25. | — 1,36. | 0,68. | |||
16,3. | 0,5. | 0,25. | — 0,36. | — 0,18. | |||
19,9. | 1,5. | 2,25. | 3,24. | 4,86. | |||
14,4. | 2,5. | 6,25. | — 2,26. | — 5,65. | |||
18,7. | 3,5. | 12,25. | 2,04. | 7,14. | |||
20,7. | 4,5. | 20,25. | 4,04. | 18,18. | |||
сумма. | 166,6. | 82,5. | 26,6. | ||||
среднее. | 5,5. | 16,66. | |||||
В результате ручного расчета получено линейное уравнение зависимости yt (урожайности) от t (время) в виде:
Y(t) = 14,89 + 0,32t.
Оценка параметров модели средствами мастера диаграмм представлена на рис. 4.
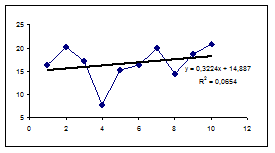
Рис. 4. Корреляционное поле и тренд
2. Оценим качество построенной модели.
Модель является адекватной, если математическое ожидание значений остатков близко или равно нулю, и если значения остаточного ряда случайны, независимы и подчинены нормальному закону распределения;
Проверка равенства нулю математического ожидания уровней ряда остатков
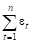
Для этого найдем значения ряда остатков и произведем суммирование (табл. 15). В нашем случае 0, поэтому гипотеза о равенстве математического ожидания значений остаточного ряда нулю выполняется.
Таблица 15
t. | Урожайность. | Yрег. | Е. | ||
16,3. | 15,20 909. | 1,90 909. | |||
20,2. | 15,53 152. | 4,668 485. | |||
17,1. | 15,85 394. | 1,246 061. | |||
7,7. | 16,17 636. | — 8,47 636. | |||
15,3. | 16,49 879. | — 1,19 879. | |||
16,3. | 16,82 121. | — 0,52 121. | |||
19,9. | 17,14 364. | 2,756 364. | |||
14,4. | 17,46 606. | — 3,6 606. | |||
18,7. | 17,78 848. | 0,911 515. | |||
20,7. | 18,11 091. | 2,589 091. | |||
сумма. | 166,6. | ||||
Модель по данному свойству адекватна.
Проверка независимости (отсутствие автокорреляции)
Данное свойство проверяют с помощью критерия Дарбина-Уотсона. Для этого находится статистика Дарбина-Уотсона (d-статистика):
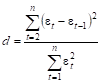
.(42).
Для проверки используют два пороговых значения dв и dн, зависящие только от числа наблюдений, числа регрессоров и уровня значимости.
Графически результат теста Дарбина-Уотсона можно изобразить следующим образом (рис. 5).
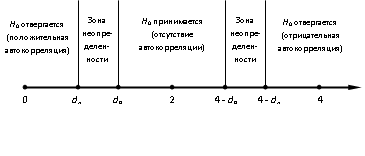
Рис. 5. Тест Дарбина-Уотсона
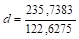
Расчетное значение d равно: = 1,9224.
Значение рассчитанного параметра d больше dв и меньше 4dв, поэтому принимаем гипотезу об отсутствии автокорреляции по критерию Дарбина-Уотсона.
Также для проверки наличия автокорреляции можно воспользоваться первым коэффициентом автокорреляции:
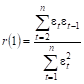
.(43).
Для принятия решения об отсутствии или наличие автокорреляции в исследуемом ряду расчетное значение r(1) сопоставляют с табличным (критическим) значением r для = 0,05. Если r(1) < r, то гипотеза об отсутствии автокорреляции в исследуемом ряду может быть принята, иначе — делают вывод о наличии автокорреляции в ряду.
Вычислим r(1) для нашего примера:
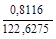
r(1) = = 0,662.
Рассчитанное значение меньше табличного. Это означает, что гипотеза об отсутствии автокорреляции в ряду урожайности может быть принята.
Модель по параметру независимости адекватна.
Проверка случайности возникновения отдельных отклонений от тренда
Используем критерий, основанный на поворотных точках. Значение случайной переменной считается поворотной точкой, если оно одновременно больше (меньше) соседних с ним элементов. Если остатки случайны, то поворотная точка приходится примерно на каждые 1,5 наблюдения. Если их больше, то возмущения быстро колеблются, и это не может быть объяснено только случайностью. Если же их меньше, то последовательные значения случайного компонента положительно коррелированны.
Критерий случайности отклонений от тренда при уровне вероятности 0,95 можно представить как.
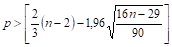
(44).
где р фактическое количество поворотных точек в случайном ряду; 1,96 квантиль нормального распределения для 5%-го уровня значимости.
Квадратные скобки означают, что от результата вычисления следует взять целую часть (не путать с процедурой округления!).
Если неравенство не соблюдается, то ряд остатков нельзя считать случайным (т.е. он содержит регулярную компоненту), стало быть, модель не является адекватной. Построим график остатков (рис. 6).
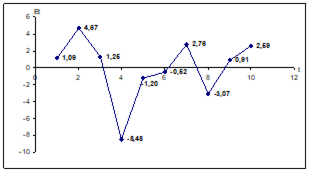
Рис. 6. График остатков
Количество поворотных точек равно 4.
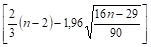
Значение = [2,9687] = 2.
Неравенство выполняется 4 > 2. Следовательно, свойство случайности выполняется. Модель по данному параметру адекватна.
Соответствие ряда остатков нормальному закону распределения
Данное соответствие можно проверить с помощью RS-критерия:
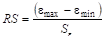
(45).
где max, min — соответственно максимальный и минимальный уровни ряда остатков; S среднеквадратическое отклонение ряда остатков.
Если расчетное значение RS попадает между табулированными границами с заданным уровнем вероятности, то гипотеза о нормальном распределении ряда остатков принимается. В этом случае допустимо строить доверительный интервал прогноза.
Среднеквадратическое отклонение ряда остатков S = 3,6912.

RS = = 3,5611.
Расчетное значение попадает в интервал [2,67−3,69], следовательно, выполняется свойство нормального распределения. Модель по этому параметру адекватна.
Если все пункты проверки дают положительный результат, то выбранная трендовая модель является адекватной реальному ряду экономической динамики, и, следовательно, ее можно использовать для построения прогнозных оценок. В противном случае модель надо улучшать.
3. Точечный и интервальный прогнозы на два шага вперед.
Точечный прогноз — это прогноз, которым называется единственное значение прогнозируемого показателя. Это значение определяется подстановкой в полученное (рассчитанное) уравнение выбранной кривой роста величины времени t, соответствующей периоду упреждения: t = n + 1; t = n + 2 и т. д.
Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность. Возникновение соответствующих отклонений объясняется следующими причинами.
- 1. Выбранная для прогнозирования кривая не является единственно возможной для описания тенденции. Можно подобрать такую кривую, которая дает более точные результаты.
- 2. Прогноз осуществляется на основании ограниченного числа исходных данных. Кроме того, каждый исходный уровень обладает еще и случайной компонентой. Поэтому и кривая, по которой осуществляется экстраполяция, также будет содержать случайную компоненту.
- 3. Тенденция характеризует движение среднего уровня ряда динамики, поэтому отдельные наблюдения могут от него отклоняться. Если такие отклонения наблюдались в прошлом, то они будут наблюдаться и в будущем.
Интервальные прогнозы строятся на основе точечных прогнозов. Доверительным интервалом называется такой интервал, относительно которого можно с заранее выбранной вероятностью утверждать, что он содержит значение прогнозируемого показателя. Ширина интервала зависит от качества модели, т. е. степени ее близости к фактическим данным, числа наблюдений, горизонта прогнозирования и выбранного пользователем уровня вероятности.
При построении доверительного интервала прогноза рассчитывается величина U(k), которая для линейной модели имеет следующий вид.
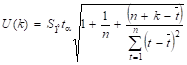
(46).
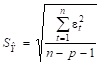
где р — число факторных переменных; k — период прогнозирования; t табличное значение t-статистики Стьюдента при заданном уровне значимости и числе наблюдений (значение t можно получить с помощью встроенной функции Excel СТЬЮДРАСПОБР); стандартная ошибка (среднеквадратическое отклонение от модели).
Для других моделей величина U(k) рассчитывается аналогичным образом, но имеет более громоздкий вид. Как видно из формулы, величина U зависит прямо пропорционально от точности модели, коэффициента доверительной вероятности t, степени углубления в будущее на k шагов вперед, т. е. на момент t = n + k, и обратно пропорциональна объему наблюдений. Доверительный интервал прогноза будет иметь следующий вид:
Uy = U(k)(47).
Если построенная модель адекватна, то с выбранной пользователем вероятностью можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадает в интервал, образованный верхней и нижней границей.
После получения прогнозных оценок необходимо убедиться в их разумности и непротиворечивости оценкам, полученным иным способом.
Построим прогнозы на два шага вперед (k = 1 и k = 2):
точечный
у11 = 14,887 + 0,32 211 18,39.
у12 = 14,887 + 0,32 212 18,71.
интервальный
Рассчитаем стандартную ошибку = 3,915.
Тогда значение U(k) для расчета доверительного интервала будет равно:
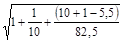
U(1) = 3,915 1,108 = 5,254;
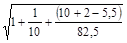
U(2) = 3,915 1,108 = 7,319.
Данные расчета верхних и нижних границ доверительного интервала приведены в табл. 8.
Таблица 16
n + k | U(k). | Прогноз. | Верхняя граница. | Нижняя граница. | |
10 + 1. | 5,254. | 18,39. | 23,644. | 13,136. | |
10 + 2. | 7,319. | 18,71. | 26,029. | 11,391. | |
4. График фактических данных, результатов расчета и прогнозирования. Для построения графика прогнозирования воспользуемся инструментом Excel Мастер диаграмм.
Для этого необходимо:
- 1. Выделить диапазоны ячеек значений t, урожайности и оценки урожайности.
- 2. Запустить Мастер диаграмм, в диалоговом окне мастера выбрать тип диаграммы Точечный, на котором значения соединены отрезками. Далее в мастере установить необходимые настройки и параметры. Желательно для исходных значений у задать параметр, который обозначает фактические значения урожайности.
- 3. В диалоговом окне Исходные данные на вкладке Ряд добавить ряды для значений точечного и интервального прогноза. Для этого выбрать кнопку Добавить, в поле Имя указать название ряда, в поле Значение Х диапазон прогноза (11 и 12), в поле Значение Y диапазон либо точного, либо интервального прогнозов. Пример окна (рис. 7).
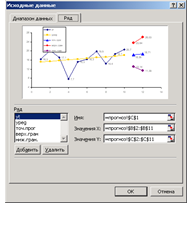
Рис. 7. Рабочее окно исходных данн…