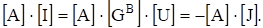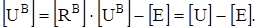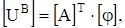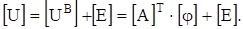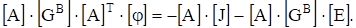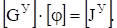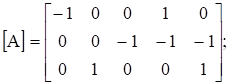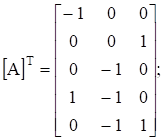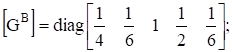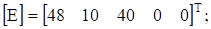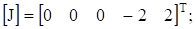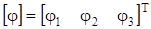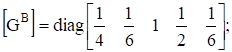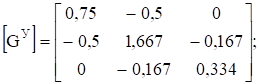Матричная форма записи метода узловых потенциалов

Уравнение для узловых потенциалов выводят из уравнений, составленных по первому закону Кирхгофа для исследуемой схемы.

Подставив в матричное уравнение (3.15) матрицу I из (3.11). получим.

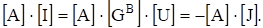
(3.25).

Уравнение (3.12) с учётом (3.10) может быть записано в такой форме.

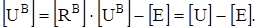
(3.26).

Можно показать, что с помощью транспонированной узловой матрицы А^Т, матрица напряжений ветвей схемы U^B может быть выражена через матрицу потенциалов узлов в таком виде.

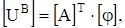
(3.27).

где — столбовая матрица потенциалов узлов схемы.

Уравнение (3.26). переписанное относительно матрицы U и с учётом (3.27). запишем так.

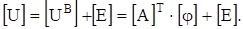
(3.28).

Теперь уравнение (3.25) с учётом (3.28) примет вид.

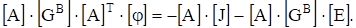
(3.29).

Произведение матриц АG^ВА^Т даёт матрицу узловых проводимостей G^У, а правая часть уравнения (3.29) представляет собой матрицу узловых токов J^У. Теперь уравнение (3.29) примет вид.

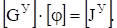
(3.30).

При составлении матрицы G^У следует учесть, что g_ii > 0, g_ik < 0 (см. уравнение 1.17).

Уравнения (3.28) и (3.29) являются узловыми уравнениями в матричной форме.

Матрицы уравнения (3.29) наиболее простые для составления, поэтому для ввода матриц в ЭВМ пользуются именно этим уравнением.

После решения уравнения (3.29) на ЭВМ относительно потенциалов, решается уравнение (3.27) относительно U^B, далее (3.28) относительно U и (3.11) относительно I.

Перечисленные матрицы выводятся в качестве выходных данных.

Пример 3.2. Для схемы рис. 3.1 составить необходимые матрицы для определения токов в резисторах методом узловых потенциалов с целью вывода их в ЭВМ. Параметры элементов схемы те же, что и в примере 3.1.

Для решения матричного уравнения (3.29) запишем следующие матрицы:

Узловую.

транспонированную узловую.

матрицу проводимостей ветвей.

матрицу ЭДС ветвей.

матрицу токов источников тока.

матрицу потенциалов узлов 1, 2, 3 на графе рис. 3.2, приняв за базисный узел 4,.

положив ₄ = 0 .

Задачи для самостоятельного решения (к главе 3)

Для схемы рис. 3.1 записать:

• а) матрицу проводимостей ветвей [G^B];
• б) матрицу узловых проводимостей [G^У];
• в) определить потенциалы узлов, приняв ₄ = 0.

Ответы: а).

б).

в) ₁ = 44 В, ₂ = 38 В, ₃ = 8 В.