Виды колебаний. 
Виды колебаний

Колебаниями называются процессы, характеризуемые определённой повторяемостью со временем. Можно без преувеличения сказать, что мы живём в мире колебаний и волн. Действительно, живой организм существует благодаря периодическому биению сердца, наши лёгкие колеблются при дыхании. Человек слышит и разговаривает вследствие колебаний его барабанных перепонок и голосовых связок. Световые волны (колебания электрических и магнитных полей) позволяют нам видеть. Другими важными примерами являются переменный ток, электромагнитные колебания в колебательном контуре, радиоволны и т. д. Как видно из приведённых примеров, природа колебаний различна. Однако они сводятся к двум типам механическим и электромагнитным колебаниям. Оказалось, что, несмотря на различие физической природы колебаний, они описываются одинаковыми математическими уравнениями.

Любая система, способная колебаться или в которой могут происходить колебания, называется колебательной. Колебания, происходящие в колебательной системе, выведенной из состояния равновесия и представленной самой себе, называют свободными колебаниями. Свободные колебания являются затухающими, так как энергия, сообщённая колебательной системе, постоянно убывает. Рассмотрим сначала колебания, полностью пренебрегая причинами, приводящими к убыванию энергии.

Гармоническими называют колебания, при которых какая-либо физическая величина, описывающая процесс, изменяется со временем по закону косинуса или синуса:

(t) = Acos (₀t +) (1).

Выясним физический смысл постоянных A, w и a, входящих в это уравнение.

Константа A называется амплитудой колебания.

Амплитуда это наибольшее значение, которое может принимать колеблющаяся величина. Согласно определению, она всегда положительна.

Выражение wt + a, стоящее под знаком косинуса, называют фазой колебания. Она позволяет рассчитать значение колеблющейся величины s в любой момент времени. Постоянная величина a представляет собой значение фазы в момент времени t = 0 и поэтому называется начальной фазой колебания. Значение начальной фазы зависит от выбора начала отсчёта времени. Величина w получила название циклической частоты, физический смысл которой связан с понятиями периода и частоты колебаний.

Периодом незатухающих колебаний называется наименьший промежуток времени, по истечении которого процессы повторяются, или коротко время одного полного колебания. Число колебаний, совершаемых в единицу времени, называют частотой колебаний. Частота n связана с периодом T колебаний соотношением.

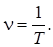
(2).

Частота колебаний измеряется в герцах (Гц). Циклическая частота связана с периодом и частотой колебаний соотношением:

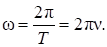
(3).

Из этого соотношения следует физический смысл циклической частоты. Она показывает, сколько колебаний совершается за 2p секунд.

Пружинный маятник представляет собой тело массой, подвешенное на пружине. Массой пружины и силами трения пренебрегаем.

Рассмотрим превращения энергии, происходящие при колебании такого маятника. Уравнение колебаний пружинного маятника имеет вид:

x (t) = Xmcos (w_t + a) (4).

где Xm и w0 амплитуда колебания и циклическая частота колебания (см. (1)). Это выражение получается из (1) заменой x на x———и A на Xm, учитывая, что.

Здесь k коэффициент жёсткости пружины, т — масса тела. Полная механическая энергия W пружинного маятника представляет собой сумму кинетической энергии Wk тела и потенциальной энергии Wp деформированной пружины, т. е.

W = Wk + Wp (5).

Потенциальная энергия деформированной пружины находится по формуле.

W_p = kx2 /2.

где x величина удлинения пружины, равная отклонению тела от положения равновесия. С учётом (4) получаем:

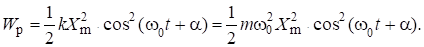
(6).

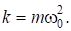
так как Кинетическая энергия тела равна Wk = (½)m2. Согласно определению скорость тела при движении вдоль координатной оси x равна.

Тогда скорость тела, совершающего гармонические колебания по закону (4), находим по формуле:

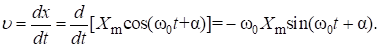
Поэтому:

(7).

Подставляя (6) и (7) в (5), находим.

(8).

поскольку sin2(w0t + a) + cos2(w0t + a) = 1. Таким образом, как следует из (8), полная механическая энергия при свободных гармонических колебаниях не зависит от времени, т. е. остается величиной постоянной. Из соотношений же (6) и (7) вытекает, что потенциальная и кинетическая энергии изменяются со временем пропорционально cos2(w0t + a) и sin2(w0t + a) соответственно. Поэтому, когда одна из них увеличивается, другая уменьшается. Следовательно, в процессе механических колебаний происходит периодический переход потенциальной энергии в кинетическую энергию и обратно. Важно отметить, что энергия колебаний пропорциональна квадрату амплитуды колебаний (см. (8)).

Колебательным контуром называют электрическую цепь, состоящую из индуктивности и ёмкости. Электрическим сопротивлением контура пренебрегаем.

Рассмотрим теперь электромагнитные колебания в колебательном контуре. Уравнение колебаний заряда q на конденсаторе записывается в виде:

q = qmcos (w0t + a) (9).

где qm амплитуда колебания заряда, ?0 циклическая частота колебаний (см. (1)).

Циклическая частота находится по формуле.

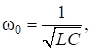
где L индуктивность катушки, С — ёмкость конденсатора.

Энергия W колебательного контура складывается из энергии WE электрического поля конденсатора и энергии WB магнитного поля индуктивности, т. е.

W = WE + WB (10).

Но.

WE = q2/(2C).

где q величина заряда на конденсаторе, C ёмкость конденсатора. Учитывая (9), получаем, что:

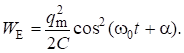
(11).

Энергия магнитного поля находится по формуле.

WB = Li2/2.

Здесь i сила тока, проходящего через проводник. Сила тока i в контуре находится дифференцированием соотношения (9) по времени:

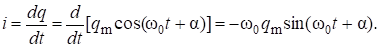
Тогда.

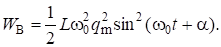
Поскольку то.

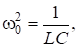
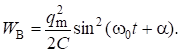
(12).

Подставляя (11) и (12) в (10), находим.

(13).

Из соотношений же (11) и (12) следует, что энергии электрического и магнитного полей изменяются со временем пропорционально cos2(?0t + ?) и sin2(?0t + ?) соответственно. Поэтому, когда одна из них увеличивается, другая уменьшается. Следовательно, в процессе колебаний происходит периодический переход энергии электрического поля в энергию магнитного и обратно, т. е. происходят электромагнитные колебания. Важно отметить, что энергия колебаний также пропорциональна квадрату амплитуды.

Затухающие колебания. До сих пор были рассмотрены идеализированные незатухающие колебания, которые возникали в колебательной системе, когда не происходит потери энергии. Однако такие потери всегда есть вследствие наличия сил трения и нагревания проводников в колебательном контуре. Рассмотрим теперь реальные колебательные системы, в которых наблюдается убывание энергии, сообщённой ей. Уравнение колебаний в этом случае записывается в виде:

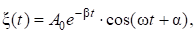
(14).

где введено обозначение.

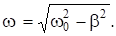
Здесь w представляет собой циклическую частоту затухающих колебаний, а w0 собственную циклическую частоту, в отсутствии потерь энергии при колебаниях. График зависимости (14) показан на рис. 1).

незатухающий колебание маятник декремент.

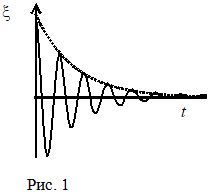
Из графика видно, что величина? периодически достигает максимума и минимума. В этом смысле процессы, описываемые уравнением (14), можно считать колебательными. Их называют затухающими колебаниями. Наименьший промежуток времени T, через который повторяются максимумы (или минимумы) называют периодом затухающих колебаний. Выражение.

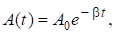
(15).

стоящее перед периодической функцией cos (t +) в формуле (14), рассматривают как амплитуду затухающих колебаний. Она экспоненциально убывает со временем (см. пунктирную кривую на рис. 1). Величина A0 представляет собой амплитуду колебания в момент времени t = 0, т. е. это начальная амплитуда затухающих колебаний. Величина, от которой зависит убывание амплитуды, называется коэффициентом затухания. Чем больше коэффициент затухания, тем колебания быстрее прекращаются.

Рассмотрим характеристики затухающих колебаний. Из выражения (15) теоретически следует, что амплитуда затухающих колебаний становится равной нулю при t. В связи с этим трудно охарактеризовать быстроту затухания. Поэтому вводят промежуток времени t, в течение которого амплитуда затухающих колебаний уменьшается в e раз (e 2,718 основание натуральных логарифмов), т. е. A(t)/A(t + ?) = e. Подставляя (15) в это выражение, получаем:

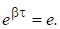
Отсюда bt = 1 и b = 1/t, т. е. коэффициент затухания обратно пропорционален времени, за которое амплитуда затухающих колебаний уменьшается в e раз.

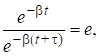
Наряду с коэффициентом затухания используется также понятие логарифмического декремента затухания.

Логарифмическим декрементом затухания называют натуральный логарифм от отношения амплитуд затухающих колебаний, соответствующих моментам времени, отличающимся на период колебания, т. е.

(16).

Выясним его физический смысл. Используя выражение (15), из (16), находим:

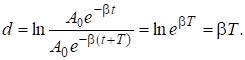
Но.

• b = 1/t
• t = NеT

где Ne число колебаний за время t.

Тогда.

d = T/ = T/(NeT) = 1/Ne.

т.е. логарифмический декремент затухания обратно пропорционален числу колебаний, по истечении которых амплитуда затухающих колебаний уменьшается в e раз.

Вынужденные колебания. Явление резонанса. Вынужденными называют колебания, происходящие под действием периодически изменяющегося воздействия, а сами воздействия называются вынуждающими. Вынужденные колебания происходят с частотой, равной частоте вынуждающих воздействий. В качестве примера рассмотрим вынужденные колебания пружинного маятника. В этом случае на тело, кроме силы упругости и трения, действует вынуждающая сила F, изменяющаяся со временем по закону.

F = Fmcos Щt,.

где Fm и Щ — амплитуда и циклическая частота колебания. Пусть циклическая частота вынуждающей силы меньше собственной частоты.

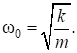
В этом случае маятник совершает гармонические колебания с некоторой амплитудой АВ. Затем начинаем плавно увеличивать частоту вынуждающей силы. При этом амплитуда вынужденных колебаний возрастает. При Щ амплитуда становится максимальной и при дальнейшем увеличении частоты амплитуда вынужденных колебаний снова уменьшается (рис. 3). Аналогичная зависимость амплитуды вынужденных колебаний от частоты наблюдается при электромагнитных колебаниях, происходящих в колебательном контуре. Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающих воздействий примерно равна собственной частоте колебательной системы, называется резонансом.

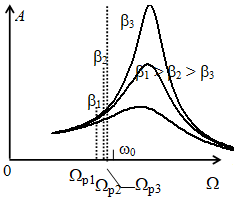
Рис 3.

Явление резонанса широко используется в технике. Оно может быть как полезным, так и вредным. Так, например, явление электрического резонанса играет полезную роль при настройке радиоприёмника на нужную радиостанцию. Изменяя величины индуктивности и ёмкости, можно добиться того, что собственная частота колебательного контура совпадёт с частотой электромагнитных волн, излучаемых какой-либо радиостанцией. В результате этого в контуре возникнут резонансные колебания данной частоты, амплитуды же колебаний, создаваемых другими станциями, будут малы. Это приводит к настройке радиоприёмника на нужную станцию.

С возможностью резонанса приходится считаться при сооружении мостов, производственных зданий, дымовых труб, высотных зданий и т. д. С целью ограничения разрушающего действия резонанса в производственных зданиях под агрегаты (источники вибрации) устанавливаются виброизоляторы. При расчёте высоких и гибких сооружений (дымовые трубы, висячие мосты и т. п.) на ветровую нагрузку предусматривают мероприятия по устройству обтекателей, виброгасителей. Для ограничения передачи колебаний от источника вибраций сооружениям через грунт, в грунте копают глубокие траншеи и наполняют их керамзитом, хорошо поглощающим энергию колебаний.

Волны. Представление о волнах пронизывает нашу жизнь и всю современную технику: волны на море и сейсмические волны в земле, звуковые волны, электромагнитные волны (радиоволны, свет, рентгеновское излучение) и т. д.

Волна это процесс распространения колебаний (возмущения) в пространстве. Геометрическое место точек, до которых дошли колебания, называют фронтом волны. Фронт волны представляет собой поверхность, отделяющую область пространства, в которой происходят колебания, от области, где их ещё нет. Все точки фронта волны колеблются в одинаковых фазах, поскольку колебания в них.

начинаются одновременно. Форма фронта волны может быть различной. Простейшими являются сферические и плоские волны, фронт которых соответственно сфера и плоскость Линии, вдоль которых происходит распространение волны, называются лучами. В однородных изотропных средах лучи перпендикулярны к фронту волны. Независимо от фронта волны различают волны продольные и поперечные. В продольной волне колебания происходят вдоль направления распространения; в поперечной перпендикулярно к направлению распространения. Волны, во всех точках которых совершаются гармонические колебания одинаковой частоты, называются монохроматическими волнами.