Ветвящиеся случайные процессы в квантовой оптике

Аннотация

Излагаются методы теории ветвящихся случайных процессов с непрерывным временем, применяемые в задачах квантовой оптики со счетным числом фотонов. Обсуждается методы решения системы дифференциально-разностных уравнений для переходных вероятностей в различных частных случаях, а также свойства соответствующих решений.

Ключевые слова: методы теории ветвящихся случайных процессов с непрерывным временем, задачи квантовой оптики со счетным числом фотонов.

Из системы дифференциально-разностных уравнений для можно получить уравнения для производящей функции. Для этого нужно уравнение для умножить на и просуммировать все уравнения. В результате имеем.

.

;

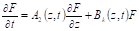
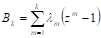
уравнение в частных производных первого порядка с коэффициентами в виде полиномов второго иго порядков от, зависимость от времени которых определяется вероятностями элементарных процессов.

Решение данного уравнения затрудняется невозможностью применения метода разделения переменных, так как полученные этим методом решения не удовлетворяют условиям. Предлагаемые в [1,2] процедуры преобразования уравнения к виду позволяющему применить процедуру разделения переменных являются частными, тем самым общее решение уравнения до сих пор не найдено.

Рассмотрим некоторые простые частные случаи. Пусть в системе имеется только один источник излучения и индуцированными процессами можно пренебречь (подобная ситуация имеет место для тормозного или магнитотормозного излучения заряженной частицы). Тогда и система дифференциально-разностных уравнений для переходных вероятностей приобретает вид:

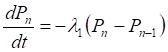
Решением данного уравнения является распределение Пуассона:

.

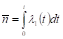
среднее представляет собой среднее число фотонов. Все корреляционные параметры для данного распределения обращаются в нуль, что отвечает однородному потоку независимых событий. Распределению Пуассона подчиняются также вклады состояний с определенным числом фотонов в когерентное излучение или отсчеты ФЭУ от источника с постоянной интенсивностью. Из других областей знания можно привести также другие примеры применимости распределения Пуассона: радиоактивный распад, число отказов элементов в большой системе, число вызовов, поступающих на АТС и т. п.

При учете индуцированного излучения, но без многофотонных процессов (), решением системы дифференциально-разностных уравнений является распределение Пойя:

.

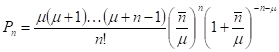
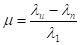
— относительная сила источника излучения. Для целых значений распределение называют отрицательным биноминальным, подчеркивая тем самым характер обобщения схемы испытаний Бернулли. Наконец при распределение переходных вероятностей имеет вид:

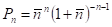
В математической литературе это распределение встречается под названием геометрического или даже распределения Фарри, но правильнее было бы называть его распределением Бозе-Эйнштейна, которое легко узнать, если заменить среднее число фотонов его явным выражением через частоту излучения.

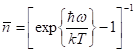
Таким образом, распределение Пойя представляет собой распределение Бозе-Эйнштейна для системы с произвольным (не целым) числом ячеек. Распределению Пойя удовлетворяют также вклады состояний с определенным числом фотонов в равновесном (черном) излучении, а также отсчеты ФЭУ от полностью хаотического (гауссова) источника света.

Среднее число фотонов в системе зависит от соотношения между вероятностями элементарных процессов.

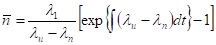
и экспоненциально возрастает при, либо экспоненциально убывает при .

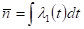
При среднее число фотонов растет практически линейным образом .

Корреляционные параметры распределения Пойя отличаются от нуля в любом порядке:

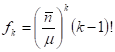
что обусловлено вкладом индуцированных процессов, в которых один фотон может рассматриваться как родоначальник другого фотона, причем любого.

Рассмотрим теперь влияние нелинейных эффектов. Пренебрегая для простоты индуцированными процессами, и полагая, имеем следующую систему дифференциально-разностных уравнений для переходных вероятностей:

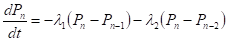
решение которой может быть записано через полиномы Эрмита следующим образом:

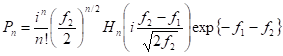
где корреляционные параметры.

;

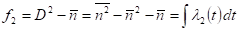
Корреляционные параметры выше второго порядка обращаются в нуль. Как легко показать, распределение фактически является дискретной сверкой двух пуассоновских распределений — одно с генерацией по одиночке, а второе — парами:

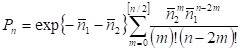
Таким образом, данный случай представляет собой суперпозицию двух источников.

Обобщение на произвольное значение очевидно — это дискретная свертка — распределений Пуассона.

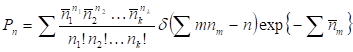
Производящая функция в данном случае может быть записана в виде произведения производящих функций отдельных распределений:

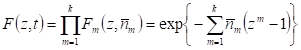
Последнее равенство получено с учетом конкретного вида производящей функции для распределения Пуассона.

Снимая ограничения на значения, получаем для производящей функции следующее выражение:

где.

Где имеет смысл среднего числа кластеров, а производящей функции распада кластера. Можно указать два предельных случая поведения (или что, то же самое, суммы в показателе экспоненты) соответствующих полностью неупорядоченному распаду (тождественным фотонам) и полностью упорядоченному распаду (нетождественным фотонам). Соответствующие производящие функции имеют вид:

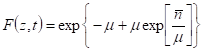
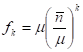
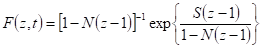
Распределение вероятностей соответствующее первой из этих производящих функций носит название усеченного Пуассонова распределения, а вторая представляет уже обсуждавшееся ранее распределение Пойя. Физический смысл данных результатов достаточно прозрачен. Заметим лишь, что усеченное Пуассоново распределение, как и распределение Пойя, имеет отличные от нуля корреляционные параметры любого порядка, что отличается от соответствующих величин для распределения Пойя лишь на постоянный множитель .

Учет индуцированных процессов приводит к весьма сложным выражениям не только для распределения переходных вероятностей, но и для производящей функции. С физической точки зрения данная ситуация отвечает лазерным системам. В простейшем случае одномодового лазера производящая функция имеет вид:

где — среднее число фотонов когерентного излучения (сигнал), — среднее число фотонов теплового некогерентного излучения (шум).

В реальных ситуациях число фотонов очень велико, поэтому вполне естественным является переход от дискретных значений к непрерывным. Непрерывные распределения случайных величин во многих отношениях отличаются от дискретных. В частности, вместо производящей функции для непрерывных распределений вводится характеристическая функция.

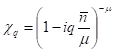
представляющая собой Фурье-образ распределения вероятностей. Факториальным моментам дискретного распределения вероятностей соответствуют начальные моменты непрерывного распределения, а корреляционным параметрам — семиинварианты.

Исследование дискретных и непрерывных распределений можно вести единым образом, поскольку как производящая функция, так и характеристическая функция могут быть представлены в виде интеграла Лебега — Стилтьеса. Для непрерывных дискретных распределений мера интеграла Лебега — Стилтьеса выражается через сумму — функций.

Характеристическая функция непрерывного распределения получается из производящей функции дискретного распределения заменой на первые члены разложения в ряд по :

С точки зрения статистической физики данный переход соответствует разложению в большой статистической сумме активности в ряд по степеням химического потенциала.

Наиболее важными дискретными распределениями являются распределения Пуассона и Пойя. Осуществляя для них переход (В.31) получаем характеристические функции вида:

;

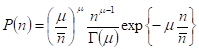
Вытекающие из них непрерывные распределения вероятностей могут быть записаны следующим образом:

;

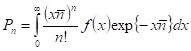
В целом ряде важных и интересных физических ситуаций системы обнаруживают так называемые масштабно-инвариантное поведение, это имеет место в гидродинамике и аэродинамике (Л.И. Седов), теории ударных волн (Л.Д. Ландау), физике твердого тела (Л. Каданов), физике высоких энергий (Р. Фейнман, З. Коба, Д. Бьёркен).

В квантовую оптику понятие масштабно-инвариантного поведения перекочевало из физики высоких энергий, где оно получило название КНО-скейлинга, по имени исследователей З. Кобы, Х. Нильсона, П. Олесена.

Масштабная инвариантность непрерывного распределения вероятностей означает, что оно представимо в виде.

где.

Очевидно, что данным свойством обладают не все распределения. Например, распределение и, соответственно, сходные распределения Пуассона и Пойя масштабно-инвариантны, а распределение нет. Усеченное Пуассоново распределение масштабно-инвариантно при условии постоянных значений .

Масштабная инвариантность дает еще один тип связи дискретных и непрерывных распределений — так называемое преобразование Пуассона, согласно которому дискретное распределение вероятности представимо в виде:

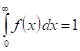
где весовая функция удовлетворяет соотношениям.

;

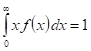
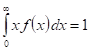
и генерирует непрерывное распределение вероятностей .

Существенным моментом в данном подходе является также то, что функция распределения является статистической функцией распределения и может быть получена как решение уравнения Эйнштейна-Фоккера-Планка. Последнее, как известно, является одним из самых фундаментальных классических кинетических уравнений не имеющее квантовомеханического аналога. Роль масштабной инвариантности и уравнения Эйнштейна-Фоккера-Планка в теории излучения изучена не до конца и необходимы дальнейшие исследования, хотя исторически первым объектом приложения уравнения Эйнштейна-Фоккера-Планка была именно задача из теории излучения — А. Фоккер исследовал распределение энергии диполя вращающегося в поле излучения.

Термин «ветвящиеся процессы» был предложен А. Н. Колмогоровым в начале 1947 года и в силу своей удачности пришёл в другие языки в виде кальки: англ. branching processes, нем. Verzweigungsprozesse, швед. исследований, связанных с разработкой атомного оружия, работы по теории ветвящихся процессов были засекречены на пять лет, в связи с опасениями, что теория может служить общей моделью неких ядерных цепных реакций, пока академик Я. Б. Зельдович не дал заключение, что работы могут быть опубликованы. Основной вклад в исследование ветвящихся случайных процессов внес Борис Александрович Севастьянов (29 сентября 1923, Москва — 30 августа 2013, там же) — советский и российский математик, доктор физико-математических наук, член-корреспондент РАН (1984) [1], а также Андрей Михайлович Зубков и другие его ученики (обзор исследований в данной области математики [2]).

Борис Александрович Севастьянов (29 сентября 1923, Москва — 30 августа 2013, там же) — советский и российский математик, доктор физико-математических наук, член-корреспондент РАН (1984). Основная область научных исследований: дискретная теория вероятностей и математическая статистика, ветвящиеся процессы, комбинаторные задачи, теория массового обслуживания. квантовый фотон пуассон В выпускном классе, случайно узнав, что на механико-математическом факультете МГУ читаются лекции по математике для школьников, прослушал лекцию Александра Геннадиевича Куроша про определители и их использование для решения системы линейных уравнений; лекцию Александра Осиповича Гельфонда о решении некоторых диофантовых уравнений, лекции Якова Семеновича Дубнова о некоторых парадоксах в математике (на первой, в частности, лектор убедительно «доказал», что каждый треугольник — равнобедренный, а на следующей лекции он разоблачил это «доказательство»). Начал посещать математический кружок Сергея Борисовича Стечкина (в то время — студента 3-го курса) и Николая Михайловича Коробова (соответственно, студента 5-го курса). На занятиях познакомился с другим участником кружка Олегом Вячеславовичем Локуциевским. Участвовал в последней предвоенной VII Московской математической олимпиаде. Принял твердое решение поступать только на мехмат. 1 сентября 1941 года, как отличник учёбы был принят в Московский университет без экзаменов. Начались лекции, но 13 или 14 октября было объявлено, что занятия прекращаются, университет эвакуируется в Ашхабад. Участвовал в сооружении защитных укреплений на подступах к Москве, с декабря 1941 года по февраль 1942 года работал штамповщиком в производственной артели Промтехсвязь. В начале февраля 1942 года вновь стал учиться в МГУ, где возобновились занятия. Перед началом экзаменов за второй курс был мобилизован в армию, служил охранником в Краснопресненской пересыльной тюрьме. Затем поступил на второй курс в Московский институт стали, а через год перевелся на третий курс механико-математического факультета МГУ. Студентом 4-го курса стал посещать семинар А. Н. Колмогорова, под руководством которого выполнил дипломную работу. В 1948 году окончил механико-математический факультет МГУ с отличием и был рекомендован в аспирантуру в Институт математики и механики МГУ. С 1948 года работал в Математическом институте им. В. А. Стеклова. В 1968 году защитил диссертацию на соискание учёной степени доктор наук. С 1969 года — профессор МГУ. Умер 30 августа 2013 года, не дожив месяц до своего 90-летия. Похороны прошли 4 сентября на Троекуровском кладбище.

Андрей Михайлович Зубков (Родился 30 декабря 1946 года, Москва) — советский и российский учёный-математик. Доктор физико-математических наук, академик Академии криптографии Российской Федерации (1991), член редакционных коллегий журналов «Теория вероятностей и ее применения», «Дискретная математика», «Математические вопросы криптографии». Область научных интересов: ветвящиеся процессы, предельные теоремы для распределений сумм случайных величин, вероятностно-комбинаторные задачи, цепи Маркова, неравенства и экстремальные задачи для вероятностных распределений, свойства случайных последовательностей дискретных случайных величин (в частности, связанными со схемами размещений частиц по ячейкам, анализом датчиков случайных чисел), анализ вероятностных алгоритмов, методы точного вычисления распределений статистик Окончил среднюю школу № 444 в Москве (1965), школьником занимался в математических кружках на механико-математическом факультете МГУ, занимал призовые места на Московских математических олимпиадах, в 1965 году — на VII Международной математической олимпиаде в Берлине. Окончил механико-математический факультет МГУ (по кафедре теории вероятностей) в 1970 году. Научный руководитель дипломного проекта — А. Д. Соловьев. С 1970 года работает в Математическом институте имени В. А. Стеклова (МИАН). Как соискатель (без обучения в аспирантуре) в 1972 году защитил кандидатскую диссертацию «Условия вырождения модифицированных ветвящихся процессов», научный руководитель — Б. А. Севастьянов. Доктор физико-математических наук (1982), тема диссертации «Аппроксимации зависимых случайных величин независимыми и их применения». В 1994 году возглавил Отдел дискретной математики МИАН. С 1995 года преподает на механико-математическом факультете (по совместительству), читает курсы теории вероятностей, теории случайных процессов, дополнительных глав теории вероятностей, ведет спецсеминар по дискретным задачам теории вероятностей; С 2005 года заведующий кафедрой математической статистики и случайных процессов.

Научный руководитель 5 кандидатских диссертаций. Автор и соавтор более чем 100 научных статей.

• 1. Севастьянов В. А. Ветвящиеся процессы. Наука, М., 1978, 436 с.
• 2. Прохоров Ю. В. Теория вероятностей. Наука, М., 1981, 496 с.
• 3. Ватутин В. А., Зубков А. М. Ветвящиеся процессы. I // Итоги науки и техники. Серия «Теория вероятностей. Математическая статистика. Теоретическая кибернетика». — М.: ВИНИТИ, 1985. — Т. 23. — С. 3−67.
• 4. Душутин Н. К., Мальцев В. М. Ветвящиеся процессы и модели множественной генерации адронов.//Сообщения ОИЯИ, Р2−89−375, 1989, 26с.
• 5. Душутин Н. К., Ясюкевич Ю. В. Излучение электромагнитных волн.- Иркутск: Изд-во ИГУ, 2012, 227 с.