Использование модели пространственной мультисегментной характеристики преобразования для повышения точности измерений термоанемометрических измерителей скорости потока жидкости

Для достижения высокой точности измерения значений скорости потока жидкости с помощью термоанемометрических измерителей предлагается использовать метод построения пространственной мультисегментной характеристики преобразования на основе нелинейных пространственных элементов. Модель пространственной характеристики преобразования, формируемая на основе ранее упомянутого метода, максимально адаптирована к особенностям конфигурации функции преобразования первичного измерительного преобразователя, фактически повторяя ее пространственную форму с учетом нелинейности, дрейфа нуля, влияния внешних факторов, включая температуру. Это обеспечивает низкую погрешность вычисления скорости потока жидкости. Исследование эффективности метода мультисегментной аппроксимации характеристики преобразования для термоанемометрических измерителей скорости потока жидкости проводилась на основе экспериментальное данных, полученных в процессе их градуировки при различных значениях температуры. Полученные результаты показывают, что максимальная приведенная погрешность измерения скорости потока жидкости с помощью термоанемометра с использованием мультисегментной пространственной характеристики преобразования не превышает ~ 0,45% при произвольной температуре, зафиксированной при проведении измерений.

Ключевые слова: термоанемометрический измеритель, пространственная мультисегментная характеристика преобразования, погрешность, скорость потока жидкости, аппроксимация, метод наименьших квадратов.

Повышение точности и достоверности определения значений физических величин представляет собой одну из важных задач совершенствования математических и алгоритмических методов обработки данных в микропроцессорных датчиках непрерывных физических величин [1, 2]. Проблема снижения погрешности измерений актуальна как при создании датчиков и измерительных устройств [3 — 5], так и в случае использования результатов измерений для решения задач мониторинга и управления, в том числе, оценки и прогнозирования состояния контролируемых объектов [6, 7]. Снижение погрешности измерений напрямую связано с используемой в микропроцессорном датчике моделью характеристики преобразования (градуировочной характеристики).

Обработка поступающих сигналов в микропроцессорном модуле датчика может осуществляться с использованием различных моделей характеристики преобразования, таких как кусочно-линейная аппроксимация пространственной характеристики преобразования датчика [8 — 11], матричная полиномиальная модель [2, 12, 13], аппроксимация характеристики с использованием сплайнов [14], алгоритмы нейронных сетей [15].

Характерным для большинства перечисленных моделей является использование единого представления характеристики преобразования для всей области изменения измеряемой величины и внешнего влияющего фактора (области определения характеристики) [16].

Для снижения погрешности определения скорости потока жидкости с помощью термоанемометрических измерителей (ТА) предлагается использовать метод мультисегментной аппроксимации характеристики преобразования микропроцессорного датчика [16 — 18], поскольку она лишена ряда недостатков, присущих упомянутым выше моделям, и обеспечивает высокую точность измерений.

Исследование эффективности метода мультисегментной аппроксимации характеристики преобразования для термоанемометрических измерителей скорости потока жидкости проводилась на основе экспериментальное данных, полученных в процессе их градуировки при различных значениях температуры.

Испытания проводились для двух однотипных термоанемометрических измерителей скорости потока жидкости (№ 1 и № 2) в диапазонах скоростей потоков (ориентировочно) от 1,46 м/с до 11,5 м/с для первого образца и от 1,79 м/с до 15,00 м/с для другого образца при 4-х значениях температуры для первого образца (Т ~ 23−25єС, ~ 30єС, ~ 38−39єС, ~ 45−47єС) и 6-ти значениях температуры для второго образца (Т ~ 21−23єС, ~ 25єС, ~ 30−31єС ~ 35−36єС, ~ 40−41єС, ~ 45−47єС).

Использование метода мультисегментной аппроксимации характеристики преобразования на основе моделей линейных или нелинейных пространственных элементов для вычислений значений скорости потока жидкости проводилось с учетом температуры.

Представленные данные испытаний характеризуются значительной нелинейностью при задаваемой температуре, которая изменялась в небольшом диапазоне величин относительно некоторого среднего значения. Диапазон отклонений температуры (разница между верхним и нижним значениями при задаваемом значении температуры) достигали значений в 1−2єС.

Нелинейность наблюдается на всем диапазоне изменения скорости потока жидкости.

Зависимость электрического сигнала канала измерения скорости потока U_ta ТА от температуры также имеет нелинейный характер. При увеличении температуры для одних и тех же значениях скорости потока выходной сигнал U_ta уменьшается, что на графиках рис. 1 выглядит как «сползание» характеристики, то есть сдвиг в область более низких значений измеряемого электрического сигнала.

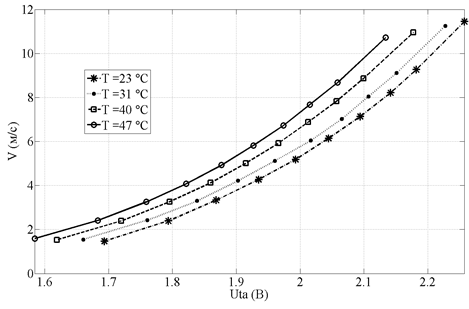
Рис. 1 Изменение сигнала ТА № 1 в зависимости от скорости потока жидкости при различных температурах

измеритель мультисегментарный термоанемометрический жидкость.

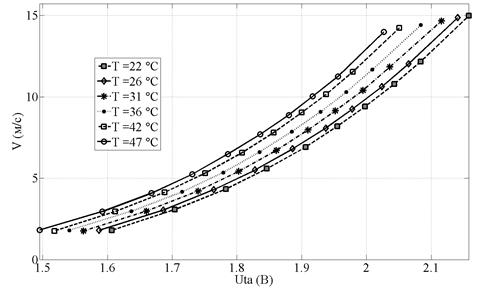
Рис. 2 Изменение сигнала ТА № 2 в зависимости от скорости потока жидкости при различных температурах

Кроме того, реальная характеристика преобразования ТА представляет вогнутую поверхность в системе параметров VU_taT, которая имеет особенность, — это вогнутая поверхность относительно области определения U_taT, границы поверхности не параллельны относительно оси 0 Т (рис. 3, 4).

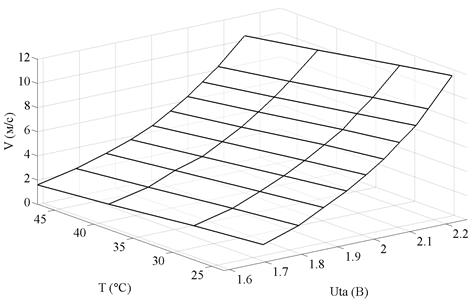
Рис. 3 Характеристика преобразования ТА № 1 в пространстве VU_taT, построенная по результатам испытаний

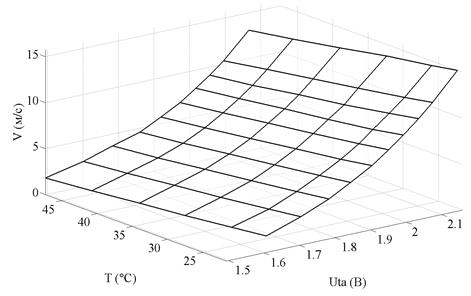
Рис. 4 Характеристика преобразования ТА № 2 в пространстве VU_taT, построенная по результатам испытаний

Пространственную мультисегментную характеристику преобразования (МСХП) для ТА формировали на основе данных испытаний следующим образом:

по параметру U_ta значения выбирались для каждой задаваемой температуры из ряда значений через один, начиная со значения, соответствующего наименьшей скорости потока жидкости;

не выбранные для построения градуировочной характеристики значения использовались для оценки точности измерений скорости потока жидкости с помощью МСХП.

Количество сегментов по оси температур 0T — 3, по оси 0U_ta — 3, т. е. всего девять сегментов.

Коэффициенты аппроксимации МСХД определяли методом наименьших квадратов для каждого сегмента с использованием экспериментальных точек, принадлежащих области определения сегмента.

На рис. 5 и рис. 6 представлены графики абсолютной величины приведенной погрешности (в процентах к диапазону измеряемой скорости движения жидкости) вычисления значений скорости движения жидкости для ТА № 1 и ТА № 2 с использованием нелинейных пространственных элементов МСХП при задаваемых температурах.

Следует отметить, что погрешность аппроксимации в данном случае значительно ниже 0,01%, что позволяет не учитывать ее при измерениях.

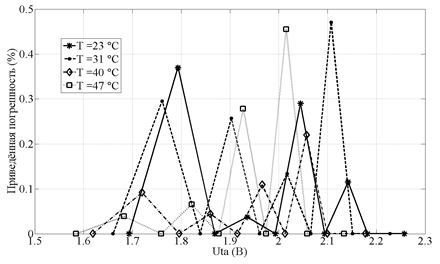
Рис. 5 Графики изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА № 1

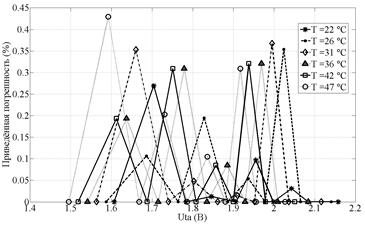
Рис. 6 Графики изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА № 2

На рис. 7 и рис. 8 представлены в пространстве параметров VU_taT графики абсолютной величины приведенной погрешности (в процентах к диапазону измеряемой скорости движения жидкости) вычисления значений скорости движения жидкости для ТА № 1 и ТА № 2 с использованием нелинейных пространственных элементов МСХП при задаваемых температурах.

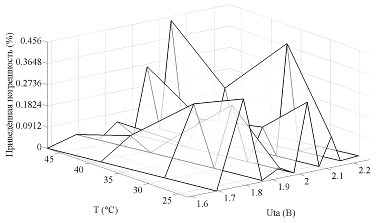
Рис. 7 График изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА № 1 в пространстве параметров VU_taT

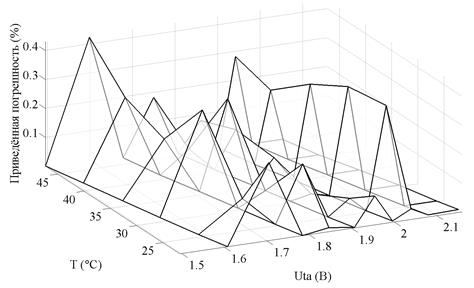
Рис. 8 График изменения абсолютного значения приведенной погрешности вычисления скорости потока жидкости с помощью мультисегментной характеристики преобразования ТА № 2 в пространстве параметров VU_taT

Таким образом, погрешность измерения скорости потока жидкости с помощью термоанемометра с использованием мультисегментной пространственной характеристики преобразования позволяет получить результат с максимальной приведенной погрешность ~ 0,45% при произвольной температуре, зафиксированной при проведении измерений.

• 1. Научно-технические, технологические и практические основы конструирования датчиковой аппаратуры для измерений физических величин: монография. Том 1. Датчиковая аппаратура давлений: монография / М.: ГОУ ВПО МГУЛ, 2010. 579 с.
• 2. Клевцов С. И., Линьков В. С., Веретельников Ю. А., Кузьминов В. Г. Погрешности вычисления давления в интеллектуальном датчике при матрично-полиномиальной аппроксимации его градуировочной характеристики // Известия Южного федерального университета. Технические науки. 2004. Т. 37. № 2. С. 30−48.
• 3. Ломакин М. А. Особенности построения модели погрешности микроэлектромеханических датчиков при решении навигационной задачи // Инженерный вестник Дона, 2014, № 2. URL: ivdon.ru/ru/magazine/archive/n2y2014/2398.
• 4. Орлов А. А., Игнатьев В. К. Цифровой емкостный дилатометр // Инженерный вестник Дона, 2011, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2011/462.
• 5. Янчич В. В., Панич А. Е., Янчич Вл.В. Перспективы применения интегрированных многофункциональных преобразователей в пьезоэлектрических датчиках механических величин // Инженерный вестник Дона, 2010, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2010/209.
• 6. Клевцов С. И. Предварительная оценка состояния совокупности параметров технического объекта с использованием интеллектуального микропроцессорного модуля // Известия Южного федерального университета. Технические науки. 2010. Т.106. № 5. С. 43−48.
• 7. Клевцов С. И. Моделирование алгоритма краткосрочного прогнозирования изменения быстроизменяющейся физической величины в реальном времени // Инженерный вестник Дона, 2012, № 3. URL: ivdon.ru/ru/magazine/archive/n3y2012/920.
• 8. Hillea P., Hцhlera R., Stracka H. A Linearisation and Compensation Method for Integrated Sensors// Sensors and Actuators A: Physical. 1994. V. 44. Issue 2. P. 95−102.
• 9. Бобровников Н. Р., Яркин С. В., Гридин Ю. Н., Стрыгин В. Д., Чертов Е. Д. Математическое обеспечение микропроцессорных преобразователей аналоговых пневматических сигналов // Приборы и системы. Управление, контроль, диагностика. 2002, № 2, С. 36−39.
• 10. Мухатаев Н. А. Алгоритм линеаризации и температурной компенсации характеристик преобразователей // Перспективные системы и задачи управления. Т.2. Таганрог: ТТИ ЮФУ, 2008. С. 74−76.
• 11. Gorbunov S. F., Tsypin B.V. Linearization of calibration characteristics of capacitance pressure sensors// Measurement Techniques. 2011. V. 53. N.10. P. 1113−1117.
• 12. Шапонич Д., Жигич А. Коррекция пьезорезистивного датчика давления с использованием микроконтроллера // Приборы и техника эксперимента. 2001, № 1, с. 54−60.
• 13. Гутников В. С. Тенденции развития электронных измерительных преобразователей для датчиков // Приборы и системы управления. 1990, № 10, С. 32−35.
• 14. Bluemm, C. Weiss, R. Weigel, R. Brenk, D. Correcting nonlinearity and temperature influence of sensors through B-spline modeling//Industrial Electronics (ISIE). 2010. IEEE International Symposium. 4−7 July 2010. P. 3356 — 3361.
• 15. Patra, J.C. Chakraborty, G. Meher, P.K. Neural-Network-Based Robust Linearization and Compensation Technique for Sensors Under Nonlinear Environmental Influences// IEEE Transactions on Circuits and Systems I: Regular Papers. 2008. V 55. Issue 5. P. 1316−1327.
• 16. Клевцов C.И. Мультисегментная пространственная аппроксимация градуировочной характеристики микропроцессорного датчика // Метрология. 2011, № 7, С. 26−36.
• 17. Клевцов C.И., Удод Е. В. Пространственная плоскостная модель градуировочной характеристики интеллектуального датчика давления // Известия Южного федерального университета. Технические науки. 2005. Т.45. № 1. С. 99−107.
• 18. Клевцов С. И. Формирование мультисегментной модели градуировочной характеристики интеллектуального датчика // Известия Южного федерального университета. Технические науки. 2008. Т. 88. № 11. С. 8−11.