Техническое проектирование арки

Данный расчет полуарок заключается в определении всех необходимых для статического расчета размеров углов наклона и их геометрических функций, так как полуарки симметричны, расчет производим для одной из них. Расчет ведется в прямоугольной системе координат с началом в центре левого узла. Ветровая нагрузка w в соответствии с дается равномерно распределенной по длине верхнего пояса арки. В связи… Читать ещё >
Техническое проектирование арки (реферат, курсовая, диплом, контрольная)
Статический расчет арки
При расчете купола не учитываем его пространственной работы, расчленим его на отдельные плоские арки пролетом 30 м и в запас прочности рассчитываем их на все виды нагрузок как плоские системы.
Определение нагрузок, действующих на балку
Нагрузки, приходящиеся на 1 м² плана здания, сведены в табл. 3.1.
Нагрузки от веса плит покрытия взяты из табл. 2.1.
Таблица 3.1 — Подсчет нагрузки на 1 м² плана здания.
Нагрузка. | Нормативная, кН/м2. | Коэффициент надежности по нагрузке. | Расчетная, кН/м2. | |
Кровля из техноэласта трехслойная и плиты покрытия. | 0,6. | ; | 0,7. | |
Собственный вес арки. | 0,1. | 1,1. | 0,11. | |
Итого постоянная. | 0,7. | ; | 0,81. | |
Временная (снеговая). | 0,88. | 1,8. | ||
Полная. | 1,58. | ; | 2,61. | |
Собственный вес арки определен в разделе «Вариантное проектирование».
Временная нагрузка взята в соответствии с [3].
Ветровая нагрузка w в соответствии с [3] дается равномерно распределенной по длине верхнего пояса арки. В связи с небольшой высотой арки она не учитывается, так как почти не увеличивает усилий действующих в сечении арки (нагрузка в виде ветрового отсоса w).
Расчет арки ведется на три вида загружения:
- 1 — временная на всем пролете и постоянная;
- 2 — временная на половине пролета и постоянная;
- 3 — временная по треугольной форме и постоянная (вариант 2, согласно [3]).
Геометрический расчет полуарок
Данный расчет полуарок заключается в определении всех необходимых для статического расчета размеров углов наклона и их геометрических функций, так как полуарки симметричны, расчет производим для одной из них. Расчет ведется в прямоугольной системе координат с началом в центре левого узла.
Основными исходными данными являются:
пролет l=30 м и высота f= 5 м.
Радиус кривизны ребер купола:
R = · (D2 + 4f2),
R = · (302+4·52) = 25 м.
Половина центрального угла дуги купола:
sinц0 = ,.
sinц0= = 0,6.
ц0 = 38_, cosц0 = 0,96.
Центральный угол 2ц0 =76_.`.
Длина дуги купола:
L = р· R,
L = = 33,14 м.
Средние кольцевые элементы, расположенные между опорным и верхним кольцами купола, образуют в плане многоугольники.
Центральный угол дуги купола между средними кольцами.
lc = 2Rsin
Отсюда:
sin = ,
sin= = 0,06.
= 3_, = 7_.
Центральный угол верхнего кольца купола:
= ц0 — 11,.
= 38_ - 113_ = 5_.
= 10_, sin10_= 0,174.
sin = sin5_= 0, 087.
Длина дуги купола, отсекаемая верхним кольцом:
Lk = R· цk ,.
Lk = 25· 0,174 = 4,35 м.
Диаметр верхнего кольца:
м.
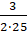

Длина дуги ребра купола на участке между опорным и верхним кольцами:
Lp = L/2 — Lk/2,
Lp = 33,14/2 — 4,35/2 = 15,72м.
Длина дуги ребра между средними кольцами:
Lс =Lp / (mк + 1),
Lс = 15,72/(3+1) = 3,95 м.
где mк = 3 — число средних колец купола.
Диаметры купола на уровнях расположения колец определяют по формуле:
di = 2· R·sinцi,,.
где цi— центральный угол между вертикальной осью купола и соответствующим рядом колец рядом.
На уровне опорного кольца d0 = D = 30 м. На уровне первого ряда колец:
d1 = 2 · 25 · sin31= 25,75 м.
Дальнейшие вычисления аналогичны изложенному и приведены в табл. 3.1. плита арка деформирование колонна Стороны многоугольника на соответствующих уровнях определяют по формуле:
ai = di · sin ,.
ai = = = 22,5_.
sin = sin11,25 = 0,195.
где = 16 — число ребер.
На уровне опорного кольца:
a0 = 30 · 0,195 = 5,85 м.
На уровне первого ряда кольца:
a1 =25,75· 0,195 = 5 м.
Дальнейшие вычисления приведены в табл. 3.1.
Проекция оси нагрузки разбивается на 16 частей от до м с шагом 1 м (рис. 8).
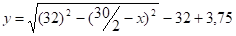
µ1 = cos1,5б, µ2 = 2sin3б [3].