Плоская деформация элементов цилиндрических конструкций под действием физических полей

Под воздействием внешних полей, таких как радиационное излучение, тепловое воздействие и т. д., физико-механические характеристики материала тела могут изменяться.

Исследованию влияния температурных и радиационных полей по отдельности на изменение модуля упругости материала, посвящены работы [1−10]. Однако практически нет работ, где вышеуказанные воздействия рассматривались бы одновременно [11].

В данной статье рассматривается влияние радиационного излучения и температурного поля на изменение модуля упругости материала как по отдельности, так и совместно. Изменение физико-механических параметров приводит так же к перераспределению напряжённо-деформированного состояния всего цилиндрического тела. В дальнейшем рассматривается бетонное цилиндрическое тело в плоской осесимметричной постановке (плоское деформированное состояние).

Основные выкладки приводятся в [11], ограничимся только главными моментами. температурный радиационный цилиндрический юнг Дифференциальное уравнение, описывающее распределение радиальных напряжений вдоль радиуса цилиндра:

(1).

Как было сказано выше, модуль Юнга зависит от температурной и радиационной нагрузок, т. е. Изменение модуля Юнга в результате температурного и радиационного воздействий определяется по формуле:

.

где k₁ и k₂ — коэффициенты, соответствующие изменению модуля Юнга в выражениях (2) и (3).

Зависимость модуля Юнга от температуры может быть аппроксимирована полиномом:

(2).

а от флюенса нейтронов описывается уравнением:

.(3).

Распределение температуры по толщине цилиндра описывается уравнением теплопроводности Фурье:

Распределение флюенса нейтронов Ф вдоль стенки цилиндра определяется уравнением Пуассона:

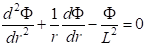
.(5).

В результате воздействия температурного и радиационного полей, в толще тела возникают вынужденные деформации, которые складываются из температурных, в результате расширения-сжатия тела, и радиационных:

.

Здесь: — вынужденная деформация; - температурная деформация; - деформация в результате радиационного воздействия; - коэффициент линейного расширения материала цилиндра.

Зависимость радиационных деформаций от дозы облучения для разных описывается эмпирической формулой:

.

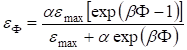
Решена задача со следующими параметрами: r_a=3.3 м; r_b=3.8 м; T_a=300^oC; T_b=0^oC, E₀=2· 10⁴ МПа; L=0.16 м; =1; =3· 10^-24 м²/нейтр.; =0.16; =0.01; =0.7; =10^{_ 24} м²/нейтр.; =0.8. Для решения задачи был использован метод конечных разностей (МКР).

На рис. 1 представлено распределение температура в толще цилиндра в соответствии с (4). В следствие малости толщины цилиндра график выглядит прямолинейным.

На рис. 2 показано распределение потока флюенса нейтронов в толще цилиндрав соответствии с (5). В результате сильного ослабления потока материалов, хорошо прослеживается спад излучения с толщиной.

Рис. 1. Распределение температуры в толще цилиндра	Рис. 2. Распределение потока флюенса нейтронов в толще цилиндра

На рис. 3 показано изменение модуля упругости материала тела. Как отмечается в работах [1, 6], изменение физико-механических параметров происходит от радиационного излучения происходит только при достижении потоком флюенса нейтронов определенного «критического» значения. Это хорошо видно на графике при 3.6 м.

График распределения модуля упругости от температуры при этом очень прямолинеен.

Рис. 3. Изменение модуля упругости в материале тела	Рис. 4. Развитие вынужденных деформаций в толще тела
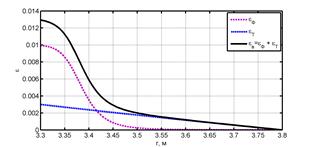Рис. 5. Изменение радиальных напряжений в толще цилиндра	Рис. 6. Изменение окружных напряжений в толще цилиндра

На рис. 4 представлены составляющие вынужденных деформаций в теле: температурной и радиационной. Как видно из графика, радиационная составляющая преобладает только на внутренней поверхности тела; температурная — равномерно распределяется по всей толщине.

На рис. 5 и 6 представлены графики распределения напряжений: радиального и окружного.

Из анализа графиков следует, что распределение напряжений в толще цилиндра не является суммой напряжений отдельных составляющих.

Таким образом, для определения напряженно-деформированного состояния цилиндрического тела, необходимо учитывать совместное влияние и температурного поля, и радиационного излучения.

• 1. Андреев В. И. Некоторые задачи и методы механики неоднородных тел: Монография — М.: Издательство АСВ, 2002. — 288 стр.
• 2. Андреев В. И., Дубровский А. В. Учёт неоднородности материала при расчете сухой защиты реактора // Вопросы атомной науки и техники. Сер. Проектирование и строительство. — М., 1982. — Вып. 3(13). — С. 3−8.
• 3. Андреев В. И., Смолов А. В. К вопросу расчета двухслойных корпусов высокого давления с учетом неоднородности материала // Сопротивление материалов и теория сооружений. — Киев: Будивельник, 1985, — Вып. 47. — С. 48_ 52.
• 4. Смолов А. В. Напряжённо-деформированное состояние неоднородных упругих цилиндров под действием силовых и температурных нагрузок. Дисс. … канд. техн. наук. — М.: 1987. — 161 с.
• 5. Возведение специальных защитных конструкций АЭС / Б. К. Пергаменщик, В. И. Теличенко. Р. Р. Темишев; под общ.ред. д.т.н., проф. В. И. Теличенко — М.: Издательский дом МЭИ, 2011. — 240 [2] с.: ил.
• 6. Строительство атомных электростанций: Учебник для вузов / В. Б. Дубровский, А. П. Кириллов, В. С. Конвиз и др.; Под ред. В. Б. Дубровского. — 2-е изд., перераб. и доп. — М.: Энергоатомиздат, 1987. — 248 с.: ил.
• 7. СНиП 2.03.04−84. Бетонные и железобетонные конструкции, предназначенные для работы в условиях воздействия повышенных и высоких температур / Госстрой СССР. — М.: ЦИТП Госстроя СССР, 1985. — 54 с.
• 8. Zhenhai Guo, Xudong Shi. Experiment and Calculation of Reinforced Concrete at Elevated Temperatures [English]. Publisher: Butterworth-Heinemann. y.2011. 226 p.
• 9. Bin Yang, Jinhua Huang, Chunjiao Lin, Xinkun Wen. Temperature Effects and Calculation Method of Closure Temperatures for Concrete-filled Steel Tube Arch Rib of Dumbbell-shape Section [Электронныйресурс] // «The Open Civil Engineering Journal», 2011, № 5, p. 179−189. — Режимдоступа: http://www.benthamscience.com/open/tociej/articles/V005/179TOCIEJ.pdf — Яз. англ.
• 10. Языев С. Б., Языев Б. М, Литвинов С. В. Реология соляного массива со сферической полостью [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 4. — Режим доступа: http://www.ivdon.ru/magazine/archive/n4p2y2012/1322 (доступ свободный). — Яз. рус.
• 11. Литвинов С. В., Козельский Ю. Ф., Языев Б. М. Расчёт цилиндрических тел при воздействии теплового и радиационного нагружений [Электронный ресурс] // «Инженерный вестник Дона», 2012, № 3. — Режим доступа: http://ivdon.ru/magazine/archive/n3y2012/954 (доступ свободный). — Яз. рус.