Выпучивание продольно сжатых стержней переменной жесткости при ползучести

Подавляющее большинство исследователей рассматривают ставший «классикой» вариант закрепления балки «шарнир-шарнир». В то же время возникает вопрос расчета стержней при других вариантах закрепления. В данной статье приводится задача, где рассматривается условия крепления стержней типа «защемление-свободный край».

Пусть на стержень действует сила F, расчетная схема задачи представлена на рис. 1. Стержень при этом может обладать некоторой начальной погибью v₀ = f (x). Размеры стержня: d диаметр сечения, l — длина стержня. Для рассматриваемых задач в качестве уравнения состояния принималось обобщенное нелинейное уравнение Максвелла для высокоэластических деформаций котороепринимает вид:

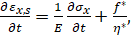
(1).

где и е — напряжения и деформации вдоль оси x

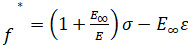
(2).

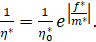
(3).

Напомним: здесь E — модуль упругости; ₀^* — коэффициент начальной релаксационной вязкости; E — модуль высокоэластичности; m^* — модуль скорости.

Одновременно с приложением силы в стержне возникают упругие деформации. Со временемдеформации увеличиваются, благодаря другим составляющим общей деформации, в частности деформации ползучести. В случае наличия возмущающих факторов (эксцентриситет в приложении силы, начальный прогиб), то наряду с деформацией сжатия имеют место и изгибные деформации, которые с течением времени приводят стержень к разрушению. максвелл деформация сечение стержень Поскольку используемое уравнение связи для полимеров является нелинейным, то применение наиболее общего и строгого метода в настоящий момент наталкивается на непреодолимые математические трудности.

Систему из пяти уравнений чл.-корр. РААСН, проф. В. И. Андреев свел к двум уравнениям относительно двух функций f^* и v

Однако разрешающие уравнения, приведенные в [1] могут быть использованы только при применении уравнения связи Максвелла-Гуревича. Поэтому необходимо получить разрешающие уравнения, лишенные этого недостатка и подходящие под любое уравнение связи. Опуская выводы, приведем разрешающее уравнение:

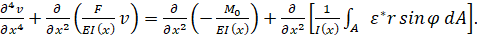
(4).

Решение данного уравнения аналитически не представляется возможным даже в случае значительных упрощений, вследствие его структуры решение удобно произвести методом конечных разностей, интегрирование проводится методом Симпсона.

Рассмотрим подробно редко рассматриваемый исследователями вариант «заделка — свободный край».

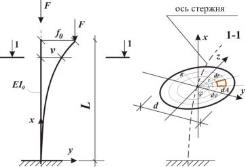
Рис. 2. ? Расчетная схема задачи при варианте закрепления «заделка_свободный край»

Задача. Рассматривается устойчивость стержни постоянного и переменного сечения при постоянной массе. Закрепление «свободный крайзаделка» Материал ПММА. Стержень имеет следующие расчётные параметры: l = 157 мм, d₀ = 15 мм, F = 70 кг, E = 294 кг/мм², f₀=0,15 мм

Граничные условия ля защемленного конца имеем:

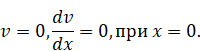
На свободном конце изгибающий момент должен обратиться в нуль:

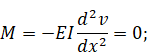
Поперечная сила на верхнем конце может быть выражена через силу F и угол поворота:

Выражая поперечную силу через прогиб и связывая ее с моментом имеем:

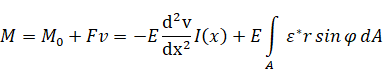
Примем за начальный прогиб.

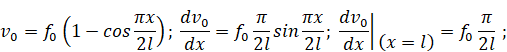
Окончательно на границе при x = l:

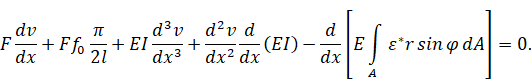
Ответ: t_кр = 2,72 часа.

Для переменного по длине стержня исходные данные:

;

;

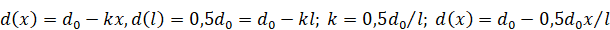
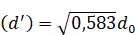
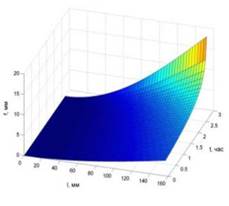
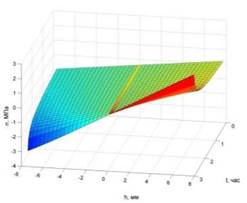
Рис. 3 Результаты расчета задачи (материал — ПММА). Рост деформаций во времени по длине стержня (а) и рост нормальных напряжений во времени по высоте переменного сечения стержня (б)

Для стержняпеременногосечения по длине можно сказать, что прогиб стремиться к конечному значению, и потеря устойчивости не происходит.

• 1. Андреев В. И. Устойчивость полимерных стержней при ползучести: [Текст]: дис. канд. техн. наук: 01.04.19: защищена 22.01. / Андреев Владимир Игоревич — М., 1967.
• 2. Вольмир А. С. Устойчивость деформируемых систем. — М.: Наука, 1975.
• 3. Языев С. Б. Устойчивость стержней при ползучести с учетом начальных несовершенств[Текст]: дис. канд. техн. наук: 05.23.17: защищена 27.10.10: утв. 21.01.11 / Языев Сердар Батырович — Р/н/Д., 2010. — 115 с.