Нечеткие теоретико-графовые подходы к моделированию и анализу социосемантических сетей знаний для задач принятия решений в научной и научно-технической экспертизе

Организации и фонды, осуществляющие финансирование проектов на конкурсной основе, в своей работе руководствуются регламентирующими документами, имеют дело с различными областями знаний, взаимодействуют с организационными структурами и персоналиями (включая экспертов фонда и научные коллективы, состоящие из руководителя и исполнителей проектов), хранят и обрабатывают многостраничные заявки и научные отчеты. В свою очередь, регламентирующие документы имеют внутреннюю и смысловую структуру, темпоральные и событийные характеристики и компоненты. Фонды используют различные многоуровневые классификаторы научных знаний. Персоналии характеризуются областью научных интересов, компетентностью и авторитетом, они объединяются в научные группы, научные школы и «незримые колледжи». При этом обрабатываемая информация, как правило, представлена в слабоструктурированном и неструктурированном виде.

Вышесказанное можно охарактеризовать множествами и подмножествами элементов и разнотипными связями с различными смысловыми и числовыми характеристиками. Прежде, чем перейти к представлению данных и знаний в системе поддержки принятия решений, необходимо выбрать промежуточный уровень абстрагирования, в котором можно было бы отобразить социальные, материальные и нематериальные компоненты и взаимосвязи. гиперграф информационный технический В работах Бруно Латура [1] и его последователей была предложена и развита акторно-сетевая теория (АСТ). Ее основной предметной областью является социология [2, 3], однако известны работы, в которых АСТ используется для представления и анализа данных в области науковедения [4] и информационных технологий.

В работах C. Roth [2] приводится теоретическое и экспериментальное обоснование феномена коэволюционной динамики социальных сетей взаимодействия (или сотрудничества) и так называемых «семантических» сетей понятий и тем. Потребность в объяснении социальных когнитивных процессов, присущих социотехническим системам, приводит исследователей к необходимости введения различных социосемантических конструктов, как-то социосемантические сети на микроуровне, социосемантические коллективы на мезоуровне и социосемантические филогенезы на макроуровне. В качестве формальных моделей таких систем выступают графы, гиперграфы и решётки, соответственно.

Градосельская [6, 7] описывает двумодальную сеть научного сообщества, в которой на одном уровне расположены акторы, а на другом — предметы (артефакты). Термин «артефакты», обозначающий контексты, в которых выражаются сетевые связи, показывает, что эти контексты порождаются связями и в этом смысле искусственны. Акторы могут быть связаны между собой, образуя сеть первого уровня. Артефакты не связаны между собой в сеть, но связаны с акторами. Один актор может быть связан с несколькими артефактами так же, как один артефакт может быть связан с несколькими акторами. Отсюда уровни связаны между собой. При более детальном анализе можно выявить связи между артефактами, опосредованные акторами. В общем итоге обнаруживаются сообщества персоналий, связанных контекстуальными переменными или артефактами.

Алгоритм построения двумодальной сети по текстовым источникам подразумевает последовательные шаги по преобразованию текста в эгоцентричные сети, эгоцентричных сетей — в общую сеть акторов, расширение общей сети акторов и, наконец, построение уровней артефактов. Каждый шаг является самостоятельным этапом анализа и может служить основанием для содержательных выводов.

Методика сетевого анализа опирается на математический аппарат теории графов и методологию анализа социальных сетей (англ. Social network analysis) [8] и может применяться для любых текстовых массивов, элементы которых связаны структурными соотношениями. В качестве «вершин» могут быть определены любые концептуальные переменные. Графические представления синтаксических и стилистических связей также можно отнести к сетям. Особым видом ориентированных сетей являются генеалогические деревья.

На этапе преобразования эгоцентричных сетей в общую сеть проводится анализ сетевого сходства двух акторов с учетом их местоположения и роли в сети, связей с другими акторами. Для этого предлагается на основе социоматрицы рассчитать эквивалентность по формуле Евклидова расстояния, предложенной Бертом. Результирующую сеть взаимных выборов, представленную графом взаимно ориентированных связей научного сообщества, предлагается рассматривать совокупно с сетью сильных связей, которая учитывает контекст упоминаний — положительный, отрицательный или неоднозначный. Такой вид сети дает больше возможностей для применения количественных методов анализа, включая индикаторы свойств сети, разработанные только для неориентированных графов [9, 10].

Однако в большинстве работ, использующих и развивающих АСТ, исследователи не доходят до уровня формального представления элементов и отношений, а ограничиваются представлением элементов и отношений на естественном языке. Ниже предлагается достаточно полный набор элементов и отношений для представления предметной области на основе графово-гиперграфовой парадигмы [11−14] и теории нечетких множеств.

Классификация типов элементов и отношений в предметной области на основе графово-гиперграфовой парадигмы и нечетких множеств. Представление неориентированных однотипных связей между простыми компонентами знаний, данных об объектах, компонентах и субъектах. Простота элементов говорит о невозможности или нецелесообразности учёта состава и внутренней структуры самого элемента. Две вершины связаны неориентированным ребром, все связи в графе имеют одинаковый смысл (принадлежность, быть частью — состоять из). Обозначим тип связи (- graphvertex). Такой граф (рис. 1а) представляется при помощи матриц (таблиц) инцидентности (- определяет, какое ребро связывает какие две вершины, где edge — ребро, vertex — вершина, — множество вершин графа, — множество рёбер графа) или смежности (- определяет какая вершина с какой вершиной связана, в неориентированном графе матрица смежности симметрична относительно диагонали, т. е. существуют связи и, элементы матрицы). Представляет интерес придание связям некоторого веса, который в нашем случае может выступать в качестве меры достоверности, точности соответствия, меры предпочтения, меры согласности (рис. 1b).

Предположим, что в качестве вершин графа у нас представлены множества высказываний экспертов относительно некоторого объекта экспертизы, тогда связям (ребрам) можно придать меру их схожести. Вычисление меры схожести можно возложить на самих авторов высказываний, на сторонних экспертов, либо на некие автоматические процедуры, например, «смысловой антиплагиат». Для случая оценки схожести самим экспертам необходимо достигать попарного согласия величины меры схожести, в противном случае при расхождении мер схожести потребуются либо процедура согласования мер (усреднение, минимум, максимум), либо использование ориентированных рёбер, каждого со своей мерой.

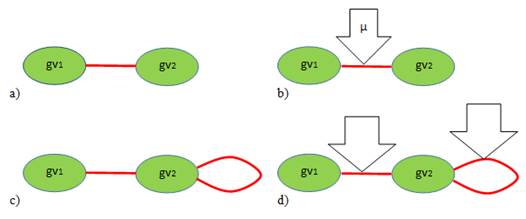
Рис. 1. Представление неориентированных связей

В этом случае матрица смежности будет состоять не из элементов множества, а из чисел отрезка. Для предмета экспертизы исследование такого нечёткого реберного графа представляет большой интерес. Исследовав различность (или похожесть) мер схожести, можно оценить или даже вычислить согласованность экспертных мнений. Наибольшая суммарная или средняя степень инцидентных конкретной вершине рёбер может характеризовать авторитетность высказывания или экспертизы в целом. Вычисление таких характеристик для всех рёбер конкретного графа позволит найти наиболее авторитетное мнение. Для некоторых случаев будет полезным удаление из графа наиболее и наименее «авторитетных» вершин. Средняя степень захода-исхода рёбер может характеризовать и самого эксперта, и меру признанности его экспертным сообществом. Величина этой меры может говорить как об уникальности эксперта или мнения, так и о его некомпетентности. Исследование графа может выявить и характеризовать группы экспертов. Сравнивая несколько экспертных графов с одинаковыми экспертами, можно вычислить авторитетность экспертов и определить лидеров или даже возможный сговор.

Представляет интерес возможность отображения рефлексивной связи в обычном (рис. 1c) и нечетком варианте (рис. 1d). Такая связь может отображать, например, факт самоцитирования или последующую оценку достоверности своего же высказывания. В матрице смежности такая связь отображается наличием 1 или на диагонали. При оценке авторитетности высказывания такую рефлексивную связь учитывать не следует.

Представление ориентированных однотипных связей между простыми компонентами знаний, данных об объектах, компонентах и субъектах. Две вершины связаны направленным или ориентированным ребром, все связи в графе имеют одинаковый смысл (например, указание влияния, убывание/возрастание степени общности, обозначение последовательности процессов и т. д.), представляются также матрицами и, но матрица смежности не симметрична, при наличии связи, , (рис. 2a). Придание связям некоторого веса (взвешенный граф), который в нашем случае может выступать в качестве меры достоверности, точности соответствия, меры предпочтения или меры согласности (рис. 1b), в случае с ориентированным ребром (дугой) представит отношение между двумя вершинами в виде вектора длиной. Путь в ориентированном графе может представлять последовательность цитирования в нескольких работах одного или нескольких авторов. Вес ребра было бы корректнее представлять в виде, то есть должно означать отсутствие связи. Мы будем придерживаться того положения, что все рассматриваемые нами графы являются полными, каждая вершина связана с каждой, но мера связности некоторых рёбер .

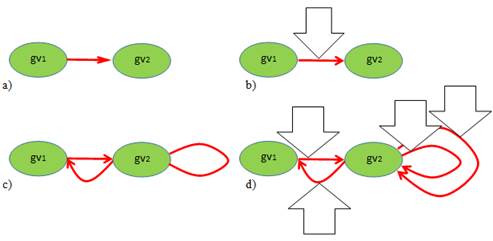
Рис. 2. Представление ориентированных однотипных связей в виде графа

Наличие связей на рис. 2c может показаться аналогичным ненаправленному ребру в графе, однако если мы придадим таким связям смысл «известность», «цитируемость» и допустим, что такие направленные отношения могут существовать в однонаправленном и двунаправленном виде, то такая модель может оказаться продуктивной. Для нечёткого реберного графа (рис. 2d) и особенно для случаев, когда, удобно придавать моделируемым отношениям смысл «взаимного влияния», «известности» или «взаимного оценивания». Для рефлексивных отношений вершин (самих к себе) смысл придания им направленности присутствует только в случае унификации вида рёбер. Рефлексивное направленное ребро нельзя обозначить ни в матрице смежности, ни в матрице инцидентности. Для отображения рефлексивности можно использовать списки. Множественные связи между парами рёбер на рис. 2c и рис. 2d представляют мультиграф, который невозможно представить двумерными таблицами. Для этого подходят многотабличные представления, многомерные таблицы, таблицы с повторяющимися или множественными полями или списки. Таблицы с повторяющимися ли множественными полями содержат отдельные поля, которые могут принимать несколько значений. Трактовка множественности значений одного поля может быть темпоральной (год, месяц), событийной (например, факт цитирования). Множественная рефлексивность (рис. 2d, достоверности и) может иметь смысл самоцитирования, либо возвращения к теме экспертизы в разные года и в разных публикациях.

Ориентированные и неориентированные связи между простыми компонентами данных. В графе присутствуют группы связей различных типов и (например, на одном и том же множестве вершин одним типом связей представлены отношения персон в штатной структуре, другим типом — отношения во временном трудовом коллективе). Направленность может означать подчиненность, а её отсутствие — равноправные отношения. Графы с такими отношениями называются смешанными. Нас интересует смысл таких парных отношений вершин. На рис. 3a представлен невзвешенный граф, неориентированное ребро которого может обозначать похожесть работ, работу авторов в одном учреждении, участие во взаимном оценивании. Одновременное наличие направленной и ненаправленной связей между двумя вершинами может обозначать одна равноправную взаимозависимость, например, работу в одном коллективе, а вторая — подчиненность в рамках конкретного проекта.

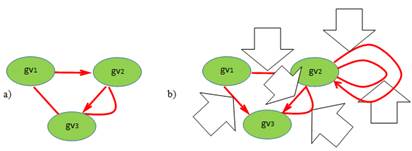
Рис. 3. Представление однотипных связей смешанным графом

На рис. 3b представлен смешанный взвешенный граф. В нем разнотипные связи присутствуют даже между двумя вершинами. Рефлексивные связи также могут быть разнотипными. Весу связи во всех случаях придаётся смысл достоверности или степени принадлежности нечеткому множеству. Степени принадлежности присутствуют в таблицах, задающих граф, либо в списках. Они могут быть постоянными либо вычисляемыми по функциям принадлежности нечётких, либо лингвистических переменных.

Представление разнотипных связей. Каждая ориентированная или неориентированная связь графа имеет своё смысловое значение, каждая связь должна быть идентифицирована (например, парные отношения сравнения заявок). В графе присутствуют группы связей различных типов и (например, на одном и том же множестве вершин одним типом связей представлены отношения персон). На рис. 4a представлен смешанный невзвешенный граф с множеством связей, причем это не просто ориентированные и не ориентированные связи, но связи с разным смыслом. Такие связи могут использоваться для представления онтологии предметной области, смысловой взаимосвязи компонентов в конкретной публикации, взаимоотношений внутри группы (групп) экспертного сообщества. Такой граф невозможно представить одной таблицей (например, смежности). Необходимо дополнительно идентифицировать тип связи. Например, граф на этом рисунке можно представить предложением: «Для исследования предположения сделаем допущение (- сделать допущение), которое само по себе вполне корректно (- корректность) и тогда получим (- получить), которое аналогично (- аналогичность), такое мы делали и ранее (- использовалось ранее)».

Рис. 4. Представление разнотипных связей в виде графа

Что касается разнотипных связей в графе, представленном на рисунке 4b, то их сопровождают меры достоверности или уверенности,. Приведем примеры интерпретации таких дуг и рёбер. Дуга может представлять в динамике различия числа публикаций по темам и, или двух авторов (экспертов).

Рис. 5. Функции принадлежности лингвистической переменной «разность числа публикаций»

Таким образом мы выразили смысловое значение дуги в виде лингвистической переменной «разность числа публикаций» на терм-множестве ={"значительно больше", «немного больше», «примерно равны», «немного меньше», «значительно меньше"} (рис. 5). Эти отношения в зависимости от знака разности можно представить двумя дугами с разными направлениями. Таким образом мы можем представить отношения в виде взвешенной дуги с меняющимися направлениями.

Представление отношений между компонентами данных и знаний в виде гиперграфа. Неориентированные ребра гиперграфа представляют подмножества некоторого множества (например, пересечение областей научных интересов, где предметная область — ребро, вершины — индивиды). Связь типа (- hypergraph) представляется на нижнем уровне при помощи матриц инцидентности — определяет какое ребро связывает какие вершины. На рис. 6a представлен такой граф. На рис. 6b представлен взвешенный вершинный граф, где каждая вершина имеет свою степень принадлежности к подмножеству, представляемому конкретным ребром. Причём, если вершина входит в несколько рёбер, то для каждого она может иметь свою степень вхождения (принадлежности). Здесь каждую персону эксперта можно идентифицировать конкретной вершиной, а ребром представить предметы экспертизы, тогда степень принадлежности может обозначать меру компетентности конкретного эксперта в конкретной тематике.

Рис. 6. Представление однотипных связей в виде гиперграфа

Представление отношений между компонентами данных и знаний в виде ориентированного гиперграфа. В ориентированных ребрах гиперграфа выделяется одна из вершин, объединённых ребром, которая имеет особый статус, связи внутри ребра «все к одному», связь типа. В ребре неориентированного гиперграфа все вершины равноправны, то есть любые две отдельно взятые вершины конкретного ребра объединяет общность принадлежности к данной ребру и их в таком смысле можно соединить дугой. В ориентированном же гиперграфе помимо принадлежности к ребру у каждой вершины существует ещё и некоторое отношение к выделенной вершине. Таким образом можно представить персон некоторой научной школы, тогда выделенной вершиной будет представлен руководитель научной школы. Имеется также возможность в одном ребре описать несколько выделенных вершин. Такое ребро гиперграфа можно считать многонаправленным. Другой способ представления направленности внутри ребра гиперграфа — указывать достоверности только для помеченных вершин в качестве степеней захода рёбер.

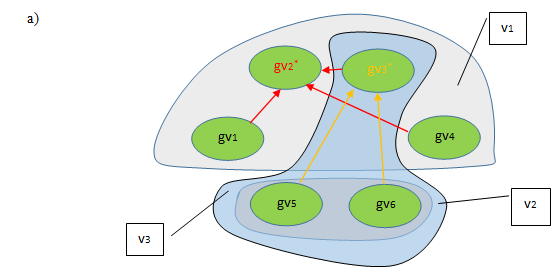
Рис. 7. Представление однотипных связей в виде оргиперграфа

Представление множественных разнотипных отношений между компонентами данных и знаний в виде иерархии графов внутри одного подмножества (ребра гиперграфа). Сложные связи внутри рёбер гиперграфа (например, ребро гиперграфа — конкурс, а вершины ребра — заявки, связанные внутри ребра гиперграфа ориентированными простыми (графовыми) ребрами в порядке возрастания значений некоторого параметра). Графовые связи внутри ребра здесь не следует рассматривать как самостоятельные, а только как описывающие некоторые свойства конкретного ребра, парные отношения вершин внутри ребра. Представление в качестве матрицы инцидентности графа может содержать ссылки на матрицы смежности, описывающие отношения вершин внутри конкретного ребра. Такие отношения внутри ребра гиперграфа являются развитием парадигмы ориентированного гиперграфа.

Для невзвешенного графа (рис. 8a) каждое ребро гиперграфа может представлять отдельный календарный год, а внутренние ориентированные связи — авторское цитирование в рамках конкретной тематики.

«Взвешенность» гиперграфа представлена в двух видах (рис. 8b): «взвешенность» вершин по отношению к ребрам и «взвешенность» графовых рёбер внутри ребра гиперграфа.

Рис. 8. Представление отношений внутри одного подмножества (ребра гиперграфа)

Представление множественных разнотипных отношений между компонентами данных и знаний в виде графов между элементами разных подмножеств (входящими в разные ребра гиперграфа).

«Графовые» связи между вершинами, входящими в разные ребра гиперграфа (например, рёбра гиперграфа — научные школы, вершины — индивиды, межрёберные связи — связи цитирования).

Если в предыдущем случае присутствуют и имеют смысл (трактование) «графовые» связи между вершинами внутри ребра, то здесь в направленные и ненаправленные связи могут быть вовлечены все вершины гиперграфа, вне зависимости в какое ребро гиперграфа они входят.

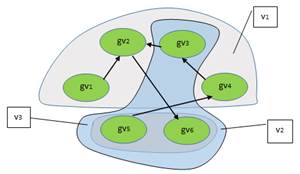
Рис. 9. Представление множественных разнотипных отношений в виде иерархии графов и гиперграфа

На практике такой гиперграф представлен двумя слоями отношений на одном и том же множестве вершин. Первый слой представлен гиперграфовыми ребрами, а второй — графовыми. Например, научные школы и цитирования одними авторами других.

Рис. 10. Представление множественных разнотипных нечетких отношений в виде иерархии графов и гиперграфа

Представление отношений между подмножествами. Связи между ребрами гиперграфа представляются несколькими матрицами. Проиллюстрируем такие типы связей. Множество вершин гиперграфа представляет акторовэкспертов, профессиональная деятельность экспертов состоит из последовательности действий (акторов) в рамках предметных областей, представленных рёбрами гиперграфа,. Актор, представленный вершиной, присутствует в двух предметных областях — рёбрах.

Рис. 11. Представление нечетких отношений внутри подмножества и между подмножествами

Связь между рёбрами представим парой. Она может обозначать зависимость одной предметной области от другой. Например, акторно-сетевая теория (АСТ) в социологии предоставила концепцию для изучения сетевой активности в сети (информатика). Для нечёткого варианта представляет собой экспертную оценку достоверности высказывания «АСТ позволяет моделировать и исследовать сетевую активность ограниченной группы акторов».

Таким образом, авторами приведено представление полного набора отношений предметной области не только между разнотипными элементами, но и между их разнородными группами. Представлены также связи между отношениями. Рассмотрены как достоверные отношения, так и частично достоверные. Комбинация отношений из такого набора позволяет строить, исследовать и использовать модели сетевой научной и научно-технической экспертизы.

Такое формализованное представление позволяет применить модели для решения множества практических задач таких как выбор экспертов, формирование экспертных групп, повышение качества экспертизы, уменьшение доли субъективности в экспертизе, анализ процесса экспертизы, анализ процессов в экспертных группах.

Дальнейшую работу авторы видят в разработке удобного компьютерного представления таких моделей и разработке алгоритмов для исследования и обеспечения функционирования моделей.

• 1. Латур Б. Пересборка социального: введение в акторно-сетевую теорию /пер. с англ. И. Полонской; под ред. С. Гавриленко; Нац. исслед. ун-т «Высшая школа экономики». — М.: Изд. дом Высшей школы экономики, 2014. — 384 с.
• 2. Малов Е. А. О концепции «актор-сети» Бруно Латура // Идеи и идеалы. — 2014. — № 1(19), т. 2. — С. 127−134.
• 3. Вахштайн В. Возвращение материального. «Пространства», «сети», «потоки» в акторно-сетевой теории // Социологическое обозрение. — 2005. — № 1, т. 4. — С. 94−115.
• 4. Артюшина А. В. Акторно-сетевая теория в бездействии: стратегии и ограничения антропологического исследования российской лаборатории // Журнал социологии и социальной антропологии. — 2010. — № 2, т. XIII. — С. 100−115.
• 5. C. Roth, J.-P. Cointet. Social and Semantic Coevolution in Knowledge Networks // Social Networks. — 2010. № 32(1), Pp. 16−29.
• 6. Батыгин Г. С., Градосельская Г. В. Сетевые взаимосвязи в профессиональном сообществе социологов: методика контент-аналитического исследования биографий // Социологический журнал. — 2001. — № 1. — С. 156−163.
• 7. Градосельская Г. В. Сетевые измерения в социологии: Учебное пособие / Под ред. Г. С. Батыгина. — М.: Издательский дом «Новый учебник», 2004. — 248 с.
• 8. Wasserman S., Faust K. Social network analysis. — Cambridge: Cambridge University Press, 1994. — 825 p.
• 9. Целых А. Н., Целых А. А. Позиционный анализ в социальных сетях на основе отношения эквивалентности // Известия высших учебных заведений. Северо-Кавказский регион. Естественные науки. Спецвыпуск. — 2011. — С. 73−76.
• 10. Tselykh, A., Veselov, G. Positional Analysis and Mapping of Scientific Networks // World Applied Sciences Journal. — 2013. — № 27(12). — Pp. 1625−1629.
• 11. Целых А. А. Графогиперграфовая модель семантической социальной сети // Известия ЮФУ. Технические науки. — 2012. — № 4(129). — С. 225−229.
• 12. Сергеев Н. Е., Целых А. А. Методы построения социосемантических сетей знаний // Современные проблемы науки и образования. — 2013. — № 6; URL: http://www.science-education.ru/113−11 462
• 13. Sergeev, N.E., Tselykh, A.A., Tselykh, A.N. Generalized approach to modeling user activity graphs for network security and public safety monitoring // SIN 2013 — Proceedings of the 6th International Conference on Security of Information and Networks. — Pp. 117−122.
• 14. Целых А. А. Теоретико-графовые модели и методы анализа семантической социальной сети для управления корпоративными знаниями и экспертизой // Обозрение прикладной и промышленной математики. — Том 18. — Москва: ТВП, 2012. — С.75.