Применения в управлении запасами

Идея «квантования» имеет применения не только в социологии. Отметим, что применять ее можно не только для выбора числа градаций. Так, весьма интересны два применения идеи «квантования» в теории управления запасами — в двухуровневой модели (полезны теоремы 1 — 3) и в классической модели Вильсона [25] с учетом отклонений от нее (демонстрируется польза «квантования» как способа повышения устойчивости). В очередной раз видим взаимопроникновение статистических методов, возникших для анализа данных из различных предметных областей, в данном случае, из социологии и логистики. Имеем еще одно доказательство того, что статистические методы — единая научно-практическая область, которую нецелесообразно делить по областям применения.

Введение

в теорию управления запасами дано, например, в [26, разд. 8.4]. В математических терминах двухуровневая однопродуктовая модель работы склада формулируется следующим образом.

Пусть — последовательность неотрицательных независимых одинаково распределенных случайных величин (последовательность величин заявок со стороны потребителей). Пусть — неубывающий кусочно-постоянный случайный процесс на, независимый от последовательности и имеющий скачки величиной 1 в точках, причем (процесс описывает моменты возникновения заявок со стороны потребителей). Положим.

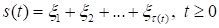
(величина s(t) показывает накопленный спрос за время t). Пусть R<0 и R+Q>0 — произвольные числа (уровни, упоминаемые в названии модели). Пусть.

.

где квадратными скобками обозначена целая часть числа. Здесь y(t) — уровень запаса продукта на складе. Предполагается, что продукт отпускается в соответствии с заявками потребителей. Когда уровень запаса на складе опускается до граничного значения R<0, мгновенно поступает новая партия продукта величиной Q. Если уровень запаса на складе при удовлетворении очередной заявки становится меньше 0, но остается больше R<0, то фиксируется образование дефицита. Рассматриваемая заявка (точнее, ее необслуженная часть) и возникающие в следующие моменты заявки накапливаются вплоть до того момента, когда суммарный дефицит достигнет граничного уровня R, а затем мгновенно удовлетворяются после прихода очередной поставки величиной Q. Таким образом,.

R < y(t) < R + Q

при всех t.

Пусть c₁, c₂, c₃ — положительные константы, T > 0. Введем функционал.

.

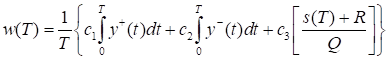
где y+ = max (y, 0) и y— = y+ - y. Требуется минимизировать M(w(T)), выбрав соответствующие R и Q.

В логистических терминах c₁ — расходы, связанные с хранением единицы продукта в течение единицы времени, c₂ — потери, порожденные дефицитом (отсутствием на складе) единицы продукции в течение единицы времени, c₃ — расходы на доставку партии продукта на склад, w(T) — средние (на единицу времени) издержки на функционирование склада (точнее, складской подсистемы, связанной со снабжением потребителей рассматриваемым продуктом). Сформулированная модель рассматривалась рядом авторов [27 — 32] при различных предположениях. У них же можно найти экономическую интерпретацию и развернутое обсуждение рассматриваемых математических объектов и констант (см. также [26, разд. 8.4]).

Будем изучать асимптотику при. Сначала найдем предельное распределение y(t).

Теорема 4. Пусть случайная величина имеет первые пять моментов и интегрируемую характеристическую функцию, при некотором С

при всех y, t таких, что R < y < R + Q и t > 0.

Доказательство. Нетрудно показать, что.

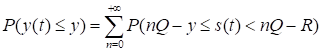
. (39).

Нам окажется полезным вытекающее из (39) представление.

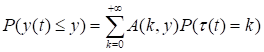
(40).

где.

.

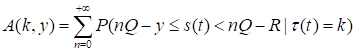
При k > 1 положим.

.

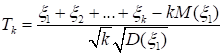
Тогда.

.

Начнем с оценки A(k, y).

Лемма 3. В условиях теоремы 4 существует константа d₁ такая, что при всех y таких, что R < y < R + Q и k = 1, 2, …, выполнено неравенство

.

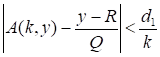
Доказательство. Пусть f_k(x) — плотность случайной величины Tk, существующая в силу условий теоремы 4. Из них же в соответствии с теоремой 2 из [33, с.611] вытекает, что.

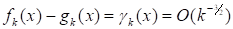
(41).

равномерно по x. Здесь.

(42).

где — плотность стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1, и — константы, зависящие от моментов случайной величины .

Для A(k, y) справедливо представление.

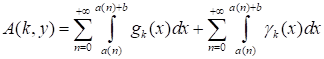
(43).

где.

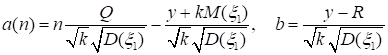
. (44).

К первому слагаемому в (43) применим лемму 2, второе слагаемое оценим с помощью (41).

Пусть m — такое целое число, что a(m) < 0, но a(m+1) > 0. Легко проверить, что для функции f(x) = gk(x — a(m)) выполнены все условия леммы 2. Полагая (слева — обозначения леммы 2, справа — обозначения из (44)).

.

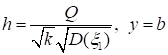
заключаем, что при некоторой константе d₂, зависящей, как видно из (42) и (44), лишь от Q и моментов, и произвольном k

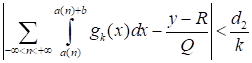
. (45).

Отметим теперь, что.

.

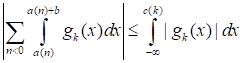
где.

.

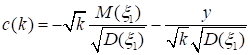
Из (42) нетрудно вывести, что.

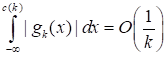
. (46).

Из (45) и (46) следует оценка.

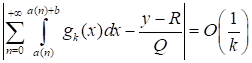
. (47).

Займемся теперь второй суммой в (43). Положим.

.

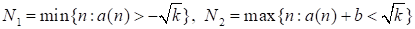
Тогда в силу (41).

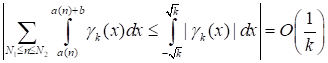
. (48).

Справедливо неравенство.

(49).

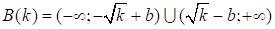
где. Первый интеграл в правой части (49) равен. С помощью неравенства Чебышева и (44) заключаем, что.

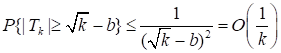
. (50).

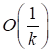
Из явного вида g_k(x), по аналогии с (46), заключаем, что второй интеграл в правой части (49) также есть. Из (48), (49), (50) и последнего утверждения следует, что.

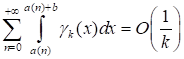
. (51).

Из (47) и (51) вытекает заключение леммы 3, поскольку, как нетрудно проверить, просматривая проведенные выше рассуждения, все оценки являются равномерными по y. Лемма 3 полностью доказана.

Продолжение доказательства теоремы 4. Из (40) и заключения леммы 3 следует, что.

.

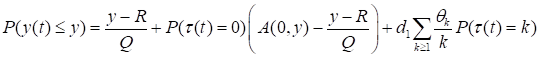
где Поскольку.

.

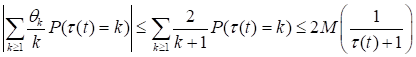
то заключение теоремы 4 справедливо при D = 2d1 + C. Теорема 4 доказана.

Теорема 5. В условиях теоремы 4 и при имеем для минимизируемого функционала

.

где

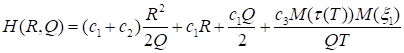
(52).

причем существуют константы d₃ и d₄ такие, что

. (53).

Доказательство. Поскольку накопленный спрос есть сумма случайного числа случайных слагаемых, то по тождеству Вальда. Следовательно, для математического ожидания третьего слагаемого средних издержек w(T) имеем.

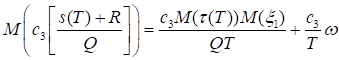
(54).

где.

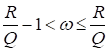
. (55).

При изучении математического ожидания первого слагаемого средних издержек w(T) полезно проинтегрировать по частям:

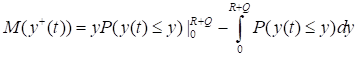
. (56).

Из (56) и заключения теоремы 4 следует, что.

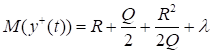
(57).

где.

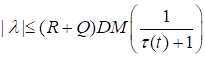
. (58).

Аналогично получаем асимптотическое выражение для математического ожидания второго слагаемого в формуле для w(T):

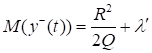
(59).

где.

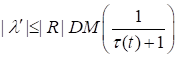
. (60).

Из (54) — (60) следует утверждение теоремы 5, при этом можно считать, что в (53).

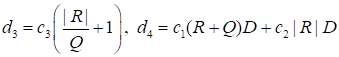
. (61).

Теорема 5 доказана.

Нетрудно показать, что H(R, Q) из теоремы 5 (см. (52)) достигает минимума по области {(R, Q): Q > 0} в точке (R0, Q0), где.

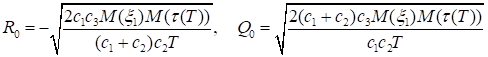
. (62).

Теорема 6. Пусть выполнены условия теоремы 5 и, кроме того,

. (63).

Предположим, что минимум M (w (T)) достигается, причем в точке (RT, QT). Тогда существует константа d5 такая, что при всех T

.

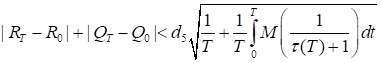
Доказательство. Нетрудно показать, что в силу (63) минимум M(w(T)) не может достигаться вне некоторого компакта. Далее, анализируя доказательства теорем 4 и 5, можно убедиться, что полученные в них оценки являются равномерными по произвольному компакту в области {(R, Q): Q > 0}. Поскольку.

.

то (R_T, Q_T) лежит в области. Эта область является эллипсом, и, как легко видеть [34],.

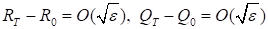
. (64).

Из (53), (61) и (64) следует требуемое. Теорема 6 доказана.

Следствие. Пусть выполнены условия теоремы 6 и, кроме того,

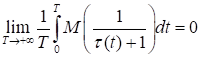
. (65).

Тогда.

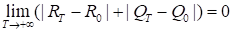
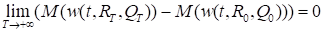
и ,.

где величину M(w(t, R_T, Q_T)) рассчитывают по формулам для математического ожидания средних издержек работы склада M(w(t)) при параметрах плана поставок R = R_T, Q = Q_T, а величину M(w(t, R₀, Q₀)) — по тем же формулам при R = R₀, Q = Q₀.

Таким образом, следствие указывает условия, при которых при большом горизонте планирования T возможно использовать асимптотически оптимальный план поставок с параметрами R = R₀, Q = Q₀, заданными формулами (62).

Отметим, что для справедливости соотношения (65) необходимо и достаточно, чтобы.

.

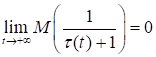
но недостаточно выполнения условия.

.

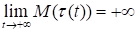
В работах [27, 31] рассматривался пуассоновский поток заявок от потребителей. Тогда накопленный спрос s(t) асимптотически (при) нормален. В этих работах предлагалось вероятности в правой части (39) заменить на предельные и полученным рядом аппроксимировать функцию распределения P(y(t) < y) при больших t. Чтобы сделать расчеты возможными, т. е. из эвристических побуждений, функция Лапласа в этом ряду заменялась [27] на ступенчатую функцию с единственным скачком в 0 единичной высоты. С помощью результатов настоящей статьи нетрудно подсчитать, что такая замена приводит к появлению лишних членов.

в аналогичном H(R, Q) выражении (обозначения [27]). Таким образом, мы отказались от предположения пуассоновости, которое редко выполняется на практике, и получили в общем случае достаточно простые формулы, попутно исправив ошибки предшественников.

Отказ от пуассоновости спроса впервые осуществлен нами в [28]. Дальнейшая работа проводилась совместно с А. В. Воскресенским [34, 35]. Настоящее изложение развивает наброски работы [36], в которой предшествующие результаты были усилены.

Классическая модель Вильсона управления запасами разобрана в [26, разд. 8.4]. Там показано, что квантование используемых экономических показателей позволяет исключить расхождение между собой методик, разработанных различными коллективами специалистов, но при этом обеспечивает сокращение издержек складского хозяйства не менее чем в 2 раза. квантование дискретный социологический Место задачи о выборе числе градаций в социологических анкетах среди других математических задач социологии обсуждается в [37].

• 1. Орлов А. И. Статистическое оценивание для сгруппированных данных // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2014. № 98. С. 1−13.
• 2. Орлов А. И. Теория нечетких множеств — часть теории вероятностей // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2013. № 92. С. 51−60.
• 3. Орлов А. И. Статистика нечетких данных // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2016. № 119. С. 75−91.
• 4. Орлов А. И. Основные идеи статистики интервальных данных // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2013. № 94. С. 55−70.
• 5. Орлов А. И., Луценко Е. В. Системная нечеткая интервальная математика. Монография (научное издание). — Краснодар, КубГАУ. 2014. — 600 с.
• 6. Орлов А. И. Асимптотика квантования и выбор числа градаций в социологических анкетах // В сб.: Математические методы и модели в социологии. — М.: ИСИ АН СССР, 1977. — С. 42−55.
• 7. Орлов А. И. Устойчивость в социально-экономических моделях. — М.: Наука, 1979. — 296 с.
• 8. Орлов А. И. Устойчивые экономико-математические методы и модели. -Saarbrьcken (Germany), Lambert Academic Publishing, 2011. — 436 с.
• 9. Орлов А. И. Новый подход к изучению устойчивости выводов в математических моделях // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2014. № 100. С. 146−176.
• 10. Орлов А. И. Прикладная статистика. — М.: Экзамен, 2006. — 672 с.
• 11. Орлов А. И. Теоретические инструменты статистических методов // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2014. № 101. С. 253−274.
• 12. Шубкин В. Н. Социологические опыты. — М.: Мысль, 1970. — 256 с.
• 13. Шошин П. Б. Размытые числа как средство описания субъективных величин // Статистические методы анализа экспертных оценок. — М.: Наука, 1977. — С. 234−250.
• 14. Саганенко Г. И. Надежность результатов социологического исследования. — Л.: Наука, 1983. — 180 с.
• 15. Шляпентох В. Э. Проблемы достоверности статистической информации в социологических исследованиях. — М.: Статистика, 1973. — 144 с.
• 16. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. Учебник. — М.: Наука, 1972. — 496 с.
• 17. Гнеденко Б. В. Курс теории вероятностей: Учебник. 7-е изд., исправл. — М.: Эдиториал УРСС, 2001. 320 с.
• 18. Лоэв М. Теория вероятностей. — М.: ИЛ, 1962. — 720 с.
• 19. Орлов А. И. Предельная теория непараметрических статистик // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2014. № 100. С. 31−52.
• 20. Моргенштерн О. О точности экономико-статистических наблюдений. — М.: Статистика, 1968. — 396 с.
• 21. Титма М. Х., Тоодинг Л. М. Математические методы в арсенале социолога. / Социологические исследования. 1986. № 4. С.123−128.
• 22. Глотов В. А., Павельева В. В. Векторная стратификация. — М.: Наука, 1984. — 94 с.
• 23. Ильясов Ф. Н. Экспериментальное обоснование количества делений шкалы. / Социологические исследования. 1984. № 4. С.113−116.
• 24. Литвак Б. Г. О выборе делений шкалы. — В сб.: Статистические методы анализа экспертных оценок. — М.: Наука, 1977. — С.228−234.
• 25. Орлов А. И. Оптимальный план управления запасами нельзя найти на основе формулы квадратного корня // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2015. № 106. С. 270−300.
• 26. Орлов А. И. Организационно-экономическое моделирование: учебник: в 3 ч. Ч.3. Статистические методы анализа данных. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2012. — 624 с.
• 27. Лавренченко А. С. Решение задач оптимального управления запасами при нестационарном пуассоновском потоке требований. // Сб. научных трудов / Московский авиационный институт. — 1974. — Вып.306. — С. 62−72.
• 28. Орлов А. И. Отказ от пуассоновости спроса в одной модели управления запасами // Исследования по вероятностно-статистическому моделированию реальных систем. — М.: Изд-во ЦЭМИ АН СССР, 1977. — С. 93−96.
• 29. Ротарь Г. В. Об одной задаче управления резервами // Экономика и математические методы. 1976. Т.12. № 4. С. 733−739.
• 30. Ротарь Г. В. Одна задача об управлении резервами // Теория вероятностей и ее применения. 1972. Т.XVII. Вып.3. С.597−599.
• 31. Саульев В. К., Лавренченко А. С. Математическая теория оптимального управления запасами. — М.: МАИ, 1974. — 188 с.
• 32. Хедли Дж., Уайтин Т. Анализ систем управления запасами. — М.: Наука, 1969. — 512 с.
• 33. Феллер В.

  Введение

  в теорию вероятностей и её приложения: Том 2. — М.: Мир, 1984. — 738 с.

• 34. Воскресенский А. В. Принцип инвариантности в одной модели управления запасами / Дипл. работа (руководитель А.И. Орлов). — М.: Мех.-мат. ф-т МГУ им. М. В. Ломоносова, 1977.
• 35. Орлов А. И., Воскресенский А. В. Принцип инвариантности в одной модели управления запасами // Прикладной многомерный статистический анализ. Ученые записки по статистике, т.33. — М.: Наука, 1978. — С.307−311.
• 36. Орлов А. И. Горизонтная устойчивость двухуровневой модели управления запасами // Многомерный статистический анализ (математическое обеспечение). — М.: Изд-во ЦЭМИ АН СССР, 1979. — С.187−199.
• 37. Орлов А. И. Математические методы в социологии за сорок пять лет // Политематический сетевой электронный научный журнал Кубанского государственного аграрного университета. 2016. № 117. С. 91−119.