Уравнение диффузии. 
Процесс диффузии

Рассмотрим систему, содержащую k компонентов, при этом допустим, что i-ый компонент имеет градиент химического потенциала, который, в свою очередь, обусловлен градиентом концентрации этого компонента. По определению поток Векторные величины в работе выделены «жирным» шрифтом. j_i(x, y, z) равен количеству частиц, которое пересекает в единицу времени поверхность единичной площади, то есть.

(3).

где x, y, zпространственные координаты, tвременная координата, c_i(x, y, z) — концентрация i-ого компонента, а v_i(x, y, z) — его средняя скорость, которую выразим через подвижность u_i(x, y, z) — и вызвавшую поток силовую характеристику системы f_i(x, y, z) -, следующим образом.

(x, y, z, t) =. (4).

Прежде, чем продолжить вывод уравнения диффузии, необходимо небольшое отступление, связанное с физическим смыслом величины f_i(x, y, z).

Из курса общей физики известно, что если в пространстве определено распределение электрического потенциала ц (x, y, z), то в этом пространстве определена и его силовая характеристика E_i(x, y, z) — напряженность электрического поля, причем.

= - grad (5).

или.

= -, (5a).

где — оператор набла, который в декартовой системе координат имеет вид

=, (5b).

где, в свою очередь, i, j, k — ортогональные единичные векторы, определяющие декартову систему координат. Справедливость равенства правых частей выражений (5) и (5а) легко показать. Действительно.

=· =.

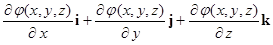
= grad.

Здесь же следует напомнить, что скалярное произведение оператора набла и некоторого вектора b (x, y, z) = b_x(x, y, z) + b_y(x, y, z) + b_z(x, y, z) определяет скалярную величину, которую называют дивергенцией.

· · =.

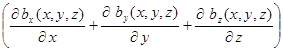
= div.

А теперь обратим внимание на следующие словосочетания: электрический потенциал, термодинамический потенциал, потенциал Гиббса. Общим для этих выражений является слово «потенциал». Этот факт не случаен и означает он не что иное как: подвергая указанные выше параметры однотипным преобразованиям, мы должны получать однотипные по физическому смыслу результаты (величины). То есть, воздействуя оператором набла на электрический потенциал, мы получаем, как было показано выше, характеристику поля, являющуюся движущей силой процессов, происходящих с заряженными частицами. Аналогично, действуя оператором набла на термодинамический потенциал, мы непременно должны получить подобный параметр. Единственно надо помнить о том, что в термодинамике количества теплоты и работы являются функциями процессов (адиабатный, изохорический, изобарический и т. д.). Поэтому, например, в изолированной системе при квазиизохорическом процессе за все изменения ответственен градиент температуры: (dU) = (?U/?S)_{V, N} dS = T dS, а в квазиадиабатном — градиент давления: (dU) = (?U/?V)_{S, N} dV = -P dV (здесь U — внутренняя энергия, S — энтропия, V — объем, N — число частиц в системе и P — давление).

В нашем случае, как мы условились ранее, поток i-ого компонента обусловлен градиентом химического потенциала м_i, поэтому.

Здесь и далее для краткости записи аргументы функций опущены за исключением тех случаев, когда это может, по мнению автора, привести к недоразумениям.= - ·. (6).

Подставив (6) в (4), а результат подстановки в (3), получим.

= -. (7).

Собственно говоря, (7) и есть первый закон Фика, записанный в самом общем виде и справедливый как для реальной, так и для идеальной систем. А теперь установим зависимость изменение количества i-ого компонента N_i от времени t в некотором локальном объеме? V в результате истечения частиц через поверхность? S, ограничивающую? V,.

В уравнении (8) знак минус поставлен вследствие того, что количество частиц в рассматриваемом объеме уменьшается со временем и, соответственно, левая часть последнего выражения должна быть меньше нуля, а под dS имеется ввиду.

(9).

где — единичный вектор, направленный нормально к элементу поверхности dS изнутри исследуемой области. Зная пространственное распределение компонентов системы c_i(x, y, z), легко рассчитать N_i

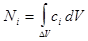
. (10).

Подставим (10) в (8).

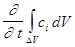
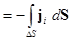
. (11).

Используя теорему Остроградского-Гаусса, в правой части (11) перейдем от интегрирования по поверхности к интегрированию по объему.

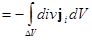
. (12).

Поскольку область интегрирования в (12) выбрана произвольно и ее размер в левой и правой частях одинаков, то равенство будет выполняться всегда в случае, когда

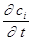
(13).

или, используя оператор набла,.

. (14).

Формулы (13) — (14) выражают второй закон Фика.

Но уравнения (7) и (13) — (14) в литературе не связывают с именем немецкого ученого Фика, поскольку указанные формулы получены для любых (идеальных и неидеальных систем), а Фиком сформулирован закон диффузии для идеальных систем, в соответствии с которым «количество соли, проходящее за известное время в направлении убывающей концентрации через некоторый элемент поверхности, пропорционально величине этого элемента, промежутку времени, величине убывания концентрации на месте нахождения элемента поверхности по направлению течения"[3].

Покажем допущения, которые необходимо сделать, чтобы от (7) и (14) перейти к традиционным уравнениям диффузии, названными законами Фика. Имея в виду, что зависимость химического потенциала от температуры Т и активности i-ого компонента имеет вид Во всех последующих формулах посредством k_Б обозначена постоянная Больцмана.

(15).

преобразуем (7) и (14) к

(16).

и.

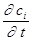
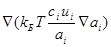
= (17).

соответственно. Применяя правила действий с дифференциальными операторами [4], получим из (17).

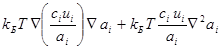
=. (18).

Для того, чтобы решить уравнение (18) относительно концентрации i-ого компонента, то есть установить зависимость от времени пространственного распределения указанного компонента для заданных начальных и граничных условий, необходимо как минимум знать пространственное распределение коэффициента активности и подвижности компонентов, образующих систему, что само по себе очень трудоемкие и в основном экспериментальные задачи. Очевидно, именно поэтому уравнение (18) не используют для указанной цели. И только для идеальных систем, когда коэффициент активности равен единице, уравнение имеет аналитические решения и то для достаточно ограниченного числа начальных и граничных условий. В случае идеальной системы выражение (7) трансформируется в.

. (19).

Три первых сомножителя в правой части (19) объединяют общим названием «Коэффициент диффузии», то есть

. (20).

В литературе равенство (20) известно как формула Эйнштейна. С учетом (20) уравнение (19) принимает ту форму записи, которую и называют первым законом Фика.

(21).

а уравнение (18) при дополнительном условии, что коэффициент диффузии не зависит от пространственных координат, принимает вид, который общепринято называть 2-м законом Фика или уравнением диффузии.

=. (22).

С учетом (20).

=. (23).

В последних двух выражениях посредством символа? (дельта) обозначен оператор Лапласа, который в декартовой системе координат имеет вид.

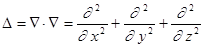
. (24).

Для того, чтобы все же учесть неидеальность системы, зависимость коэффициента активности и подвижности от пространственных координат переносят на коэффициент диффузии. Схема получения уравнения диффузии в этом случае следующая. Уже в (7) полагают, что = D_i(x, y, z) — функция пространственных координат x, y, z. А затем уравнение (7) подставляют в (17), которое принимает вид.

=. (25).

Однако аналитическое решение уравнения (25) получить не удается. В лучшем случае решение (25) можно получить в виде суперпозиции решений, отвечающих на разных пространственных интервалах различным коэффициентам диффузии. В этой связи далее будут показаны решения уравнения диффузии численными методами.