Логарифмический закон распределения скоростей в круглой трубе

На рис. 6.17 даны эпюры скорости ламинарного (1) и турбулентного (2) потоков при одинаковых расходах в круглой цилиндрической трубе. В ламинарном гидродинамическом пограничном слое турбулентного потока () имеет место линейный закон изменения скорости, а в турбулентном ядре () — логарифмический закон. В ламинарном потоке закон изменения скорости параболический. При исследовании турбулентного… Читать ещё >
Логарифмический закон распределения скоростей в круглой трубе (реферат, курсовая, диплом, контрольная)
На рис. 6.17 даны эпюры скорости ламинарного (1) и турбулентного (2) потоков при одинаковых расходах в круглой цилиндрической трубе. В ламинарном гидродинамическом пограничном слое турбулентного потока (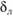 ) имеет место линейный закон изменения скорости, а в турбулентном ядре (
) имеет место линейный закон изменения скорости, а в турбулентном ядре (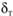 ) — логарифмический закон. В ламинарном потоке закон изменения скорости параболический.
) — логарифмический закон. В ламинарном потоке закон изменения скорости параболический.
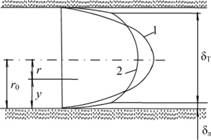
Рис. 6.17. Эпюры скоростей ламинарного и турбулентного потоков.
Выведем закон распределения скорости в круглой трубе для турбулентного потока вблизи стенки, за исключением ламинарного пограничного слоя ( ). При турбулентном движении инерционное касательное напряжение определяется, но формуле (пренебрегая напряжением от молекулярной вязкости).
). При турбулентном движении инерционное касательное напряжение определяется, но формуле (пренебрегая напряжением от молекулярной вязкости).
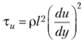 (6.14).
(6.14).
где l — длина пути перемешивания при переходе жидкости из одного слоя в другой.
Примем следующие допущения:
- 1) касательные напряжения в зоне турбулентного ядра близки к касательным напряжениям у стенки:
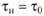 (допущение Прандтля);
(допущение Прандтля); - 2) длина пути перемешивания пропорциональна расстоянию от стенки:
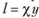 , где
, где 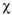 - коэффициент пропорциональности, определяемый из опыта.
- коэффициент пропорциональности, определяемый из опыта.
С учетом принятых допущений формула (6.14) примет вид.
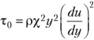 ,.
,.
или.
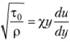
Известно, что.
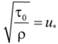 ,.
,.
где 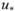 - динамическая скорость (см. параграф 6.9).
- динамическая скорость (см. параграф 6.9).
Тогда.
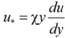
Отсюда.
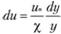
Интегрируя, получаем.
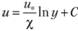 (6.15).
(6.15).
Следовательно, в области турбулентного потока около стенки скорость изменяется по логарифмическому закону (кривая 2 на рис. 6.17).
Опытом установлено, что при соответствующем выборе постоянной 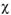 эта формула может быть распространена на все живое сечение трубы, за исключением ламинарного слоя, где скорость изменяется по линейному закону.
эта формула может быть распространена на все живое сечение трубы, за исключением ламинарного слоя, где скорость изменяется по линейному закону.
Так как формулу (6.15) можно распространить на все живое сечение трубы, то определим постоянную С из того условия, что при 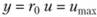
Тогда.
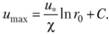 (6.16).
(6.16).
Вычитая из формулы (6.16) выражение (6.15), находим.
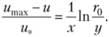
Или, переходя к десятичным логарифмам, имеем 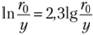 и, подставляя
и, подставляя 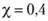 (для гладких труб), получаем.
(для гладких труб), получаем.
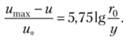 (6.17).
(6.17).
Разность umax-и называется дефицитом скорости, а выражение в левой части — относительным дефицитом. Таким образом, относительный дефицит скорости является функцией только безразмерного расстояния 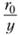
Установим соотношение между средней и максимальной скоростями. Пусть при некотором значении 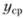 скорость жидкости равна средней скорости
скорость жидкости равна средней скорости 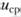 . Тогда можно записать.
. Тогда можно записать.
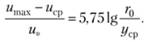
Вследствие того что относительный дефицит скорости есть всегда одна и та же функция 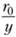 , то и средняя ордината должна пересекать кривую.
, то и средняя ордината должна пересекать кривую.
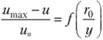
всегда в одной и той же точке с абсциссой 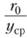 , т. е. должно быть.
, т. е. должно быть.
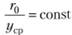
Следовательно,.
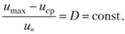 (6.18).
(6.18).
Расчеты и эксперимент показывают, что можно принять.
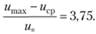 (6.19).
(6.19).
Формулы (6.17) и (6.19) позволяют производить построение эпюр скоростей в турбулентном ядре потока.
Зная 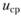 находим.
находим.
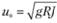 ,.
,.
где 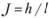 - гидравлический уклон;
- гидравлический уклон; 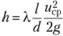 - линейные потери напора.
- линейные потери напора.
Из уравнения (6.19) находится 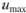 . По известным
. По известным 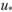 и
и 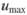 по формуле (6.17) находится величина осредненной скорости
по формуле (6.17) находится величина осредненной скорости 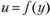
Экспериментальные данные для коэффициента гидравлического сопротивления. Опыты Никурадзе и Зегжда
При исследовании турбулентного движения жидкости в трубах необходимо решать два основных вопроса — определения потерь напора и распределения скоростей по поперечному сечению трубы. Опыты показывают, что обе эти величины существенно изменяются в зависимости от диаметра трубы, вязкости жидкости, скорости движения и шероховатости стенок труб.
Экспериментальные данные для? в широком интервале чисел Re были получены И. И. Никурадзе в трубах и А. П. Зегжда — в прямоугольных каналах с искусственной (песочной) шероховатостью.
Средний диаметр фракции песка? принимался за меру абсолютной шероховатости (рис. 6.18). Труба называется гидравлически гладкой, если средняя высота выступов шероховатости? меньше толщины ламинарной пленки 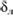 . В этом случае шероховатость не влияет на движение. Если абсолютная шероховатость? больше толщины ламинарной пленки
. В этом случае шероховатость не влияет на движение. Если абсолютная шероховатость? больше толщины ламинарной пленки 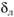 , то труба называется гидравлически шероховатой. В этом случае шероховатость существенно влияет на движение жидкости (рис. 6.19).
, то труба называется гидравлически шероховатой. В этом случае шероховатость существенно влияет на движение жидкости (рис. 6.19).
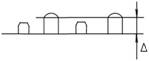
Рис. 6.18. Схема к объяснению абсолютной шероховатости.
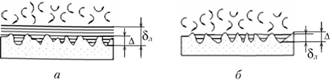
Рис. 6.19. Схемы гидравлически гладкой (а) и гидравлически шероховатой (б) труб.
Таким образом, абсолютная шероховатость Д — это средняя высота выступов шероховатости. Относительная шероховатость определяется величиной.
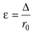
где 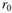 - радиус трубы.
- радиус трубы.
Величина, обратная относительной шероховатости,.
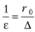
называется относительной гладкостью.
Результаты опытов представлены на графиках рис. 6.20. На графиках всю область чисел Рейнольдса можно разделить на пять характерных зон движения.
1. Зона ламинарного режима (Re < 2300, или lgRc < 3,36). Здесь все опытные точки, независимо от шероховатости стенок, ложатся на прямую линию I, описываемую уравнением Ж. Пуазейля 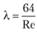
Следовательно, опытные данные позволяют заключить, что при ламинарном движении шероховатость стенок не оказывает влияния на сопротивление (коэффициент трения). Потери напора здесь пропорциональны скорости.
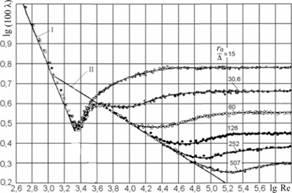
Рис. 6.20. Графики И. И. Никурадзе и А. П. Зегжда.
Действительно, подставляя выражение для коэффициента трения.
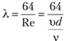
в формулу Дарси — Вейсбаха.
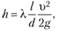
получаем.
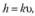
где 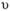 - средняя скорость;
- средняя скорость; 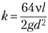
- 2. Переходная зона. Здесь ламинарный режим переходит в турбулентный (2300? Re? 3000). Коэффициент? возрастает с увеличением числа Рейнольдса, оставаясь одинаковым для различных шероховатостей.
- 3. Зона гидравлически гладких труб для турбулентного режима. Для труб с высокими значениями относительной гладкости (r0/? > 500) опытные точки для чисел Рейнольдса (400 < Re < 80r0/?) располагаются вдоль наклонной прямой II. Эта прямая известна как прямая Блазиуса для гладких труб. На ней коэффициент трения? хорошо описывается эмпирической формулой Блазиуса
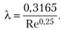
Потери напора определяют по формуле 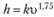
- 4. Зона шероховатых труб (r0 /? < 500), или так называемая доквадратичная зона при турбулентном режиме (80r0 /А < Re < 1000r0/А). Здесь отклонение экспериментальных точек от прямой II зависит от величины шероховатости (относительной гладкости). И это отклонение наступает тем раньше, чем меньше относительная гладкость. При этом коэффициент? стремится к некоторому пределу (разному для труб с различной шероховатостью), оставаясь затем постоянным при увеличении числа Re.
- 5. Зона вполне шероховатых труб (r0/? = 15 и r0 /? = 30). Гидравлические потери в этой области пропорциональны квадрату скорости (квадратичный закон сопротивления). Для кривых r0/? = 15 и r0/? = 30 ламинарная пленка даже при небольших значениях Re не перекрывает выступов шероховатости, и эти кривые с увеличением числа Re только пересекают линию II для гладких труб. Следовательно, в данном случае коэффициент? совершенно не подчиняется закону для гладких труб. С увеличением числа Re он постепенно возрастает и при lgRe = 4,6 для первой кривой (r0/? = 15) или lgRe = 5,0 для второй кривой (r0/? = 30) становится практически независимым от Re.
Коэффициент? для этой зоны может быть определен по формуле Шифринсона.
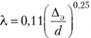
где ?э — эквивалентная шероховатость (см. ниже).
Полученным результатам можно дать следующее объяснение: до тех пор пока выступы шероховатости полностью погружены в ламинарный пограничный слой (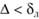 ),.
),.
для величины гидравлических сопротивлений нет разницы между гладкими и шероховатыми поверхностями стенок. Коэффициент? здесь зависит только от числа Рейнольдса и определяется как для гладких труб (1−3-я зоны).
В случае, когда выступы шероховатости выходят за пределы пограничного слоя (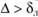 ), ламинарное течение нарушается, и выступы шероховатости оказываются в области турбулентного течения жидкости.
), ламинарное течение нарушается, и выступы шероховатости оказываются в области турбулентного течения жидкости.
С увеличением числа Рейнольдса толщина пограничного слоя уменьшается, и в случае, когда величина? оказывается сопоставимой с величиной 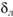 , коэффициент? зависит не только от числа Рейнольдса, но и от шероховатости стенок (4-я зона).
, коэффициент? зависит не только от числа Рейнольдса, но и от шероховатости стенок (4-я зона).
Если число Рейнольдса достаточно велико и, А значительно больше? л, то коэффициент? зависит только от шероховатости и не зависит от числа Рейнольдса (5-я зона).
Опыты А. П. Зегжды для прямоугольных каналов позволили получить график, близкий к графику И. И. Никурадзе не только качественно, но и количественно, если результаты сопоставлять при одинаковых гидравлических радиусах.
Опыты, проведенные в промышленных трубопроводах с естественной шероховатостью, показали, что оценка только по высоте выступов шероховатости, А недостаточна, большую роль имеет также характер шероховатости: форма выступов, их расположение и проч. Поэтому было введено понятие об эквивалентной шероховатости 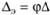 (
(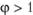 ), где параметр
), где параметр 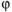 зависит от характера шероховатости. Под эквивалентной шероховатостью
зависит от характера шероховатости. Под эквивалентной шероховатостью 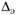 понимают такую зернистую шероховатость, при которой сопротивление оказывается таким же, как и при действительной шероховатости. Величина эквивалентной шероховатости
понимают такую зернистую шероховатость, при которой сопротивление оказывается таким же, как и при действительной шероховатости. Величина эквивалентной шероховатости 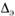 указывается в гидравлических справочниках в зависимости от типа трубопровода.
указывается в гидравлических справочниках в зависимости от типа трубопровода.