Использование средней взвешенной первых значений ряда

Из недостатков предыдущего варианта оценивания первоначального расчетного значения прогнозируемого показателя со всей очевидностью следует другой вариант, свободный от него — использование средней взвешенной первых значений ряда^[1]. Эта средняя взвешенная по логике процедуры должна находиться так, как это предопределяется логикой метода Брауна, т. е. с помощью весов, задаваемых рядом (7.4). Исследования показали, что расчет модели Брауна следует начинать не с вычисления первого расчетного значения 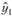, а с вычисления третьего расчетного значения, нс прибегая непосредственно к формуле Брауна, а вычисляя это значение как среднюю взвешенную: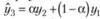

Теперь, зная расчетную величину третьего наблюдения, ее можно подставить в модель Брауна, после чего продолжать вычисления по модели для четвертого, пятого и последующих наблюдений.

Тогда, с учетом этих начальных значений модель Брауна в полной форме должна быть записана так^[2]:

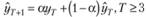при 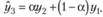(7.28).

Как видно, в этом подходе нет субъективизма, случайная ошибка первого и второго наблюдения усредняется с помощью той же постоянной сглаживания, что и для других членов ряда. Единственным недостатком такого метода является неравномерное и необоснованное распределение весов между двумя первыми наблюдениями. Так, если? мал и близок к 0, то вес у второго наблюдения становится значительно меньше, чем у первого. Если же, а близок к 1, то ситуация получается диаметрально противоположной: у второго наблюдения вес получается больше, чем у первого. Если же? вообще лежит в запредельном множестве, то у первого наблюдения получается отрицательный вес. Таким образом, четкого математического обоснования у такого метода нет, хотя он и лишен ряда недостатков других методов задания первого расчетного значения в модели Брауна.

5. Расчет значений на основе ряда весов модели Брауна. Существует еще один способ задания начального расчетного значения в модели Брауна, который логично вытекает из сути самой модели.

Как уже отмечалось ранее, сумма ряда весовых коэффициентов на практике никогда не равна единице, а может лишь приближаться к ней (исключением является случай, в котором 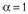). А раз так, то величина остаточного члена ряда 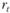в момент времени t может быть найдена по формуле.

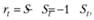(7.29).

где S — сумма бесконечного ряда, равная в нашем случае единице; St — сумма конечного ряда из его первых t членов.

Найдем, чему равен остаточный член (7.29) для двух наблюдений:

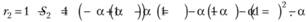
Теперь найдем величину остаточного члена для трех наблюдений:

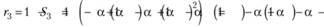
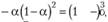
Очевидно, что для ряда наблюдений, состоящего из t членов, остаточный член будет равен.

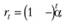(7.30).

Он будет равен нулю только тогда, когда выполняется одно из двух условий:

• 1) постоянная сглаживания равна единице;
• 2) число членов ряда стремится к бесконечности

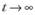
Так как ситуация равенства постоянной сглаживания единице встречается крайне редко, а бесконечных рядов в экономике не бывает, то мы приходим к выводу, что практически всегда экспоненциально взвешенная средняя по сути не будет таковой, поскольку не выполняется условие (7.4). Стало быть, весовые коэффициенты для сохранения сути модели Брауна нужно скорректировать.

Мы знаем, что сумма весовых коэффициентов в соответствии с (7.29) равна.

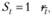(7.31).

или, учитывая (7.30),.

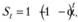
Таким образом, если мы умножим каждый весовой коэффициент в ряде (7.4) на поправочный.

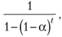(7.32).

то сумма весов S станет равной единице.

Для выборки из двух наблюдений среднее экспоненциальное взвешенное, являющееся прогнозной оценкой третьего наблюдения, будет с учетом поправки (7.32) рассчитываться так:

(7.33).

Для выборки из трех наблюдений.

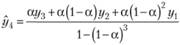
Окончательно для выборки из t наблюдений будем иметь.

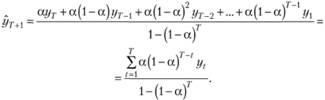(7.34).

Таким образом, исследователь может сам принять решение о том, с какого значения начинать расчет, и в таком случае в качестве первого расчетного значения использовать рассчитанное по формуле (7.34), а далее для расчета последующих значений уже использовать формулу (7.26). Например, если начинать расчеты с третьего наблюдения, то можно использовать формулу (7.33) для получения этого стартового значения.

Предложенное решение обладает несколькими преимуществами:

• 1) средняя взвешенная (7.34) представляет собой экспоненциально взвешенную первых Т значений ряда. Все последующие значения ряда также рассчитываются по формуле экспоненциально взвешенной (сама модель Брауна), в результате чего у исследователя имеется однородный ряд расчетных значений, ситуации «чужеродного вторжения» в процесс не происходит;
• 2) при подборе оптимального значения постоянной сглаживания два первых наблюдения у1 и у2 участвуют в формировании третьего значения через ту же постоянную сглаживания, через которую пропускается весь ряд наблюдений;
• 3) полностью устраняется элемент субъективизма.

Из явных недостатков такого метода можно отметить потерю первых двух расчетных значений (так как ряд начинает заполняться значениями, начиная с третьего наблюдения), которые могут понадобиться для более корректного сравнения разных моделей.

Таким образом, мы получили еще один вариант модели Брауна в полной форме с учетом начальных значений:

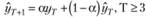при 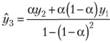(7.35).

• [1] Светуньков С. Г. Бутуханов Л. В. Светуньков И. С. Исследование запредельных случаев метода Брауна применительно к малым выборкам. СПб.: Изд-во СП6ГУЭФ, 2005.
• [2] Светуньков С. Г., Бутуханов Л. В., Светуньков И. С. Запредельные случаи метода Брауна в экономическом прогнозировании. СПб.: Изд-во СПбГУЭФ, 2006.