Аналитические многофакторные модели

Модели Фишбейна и Розенберга

Аналитические многофакторные модели, реализующие статистический подход к комплексной оценке отношения к продукту, могут иметь один из двух вариантов представления: 1) атрибутивный, основанный на субъективных оценках конкретных объективных и субъективных свойств продукта потребителями; 2) мотивационный, основанный на оценках, выражающих степень пригодности продукта для удовлетворения чувств, нужд, выгод. Соответственно атрибутивному и мотивационному вариантам в табл. 15.4 представлены две модели — Фишбейна и Розенберга.

Таблица 15.4

Модели Фишбейна и Розенберга

Аналитическая зависимость.	Модель.	Параметры модели и обозначения.
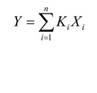	Фишбейна.	i — номер свойства; Хi — выраженность i-го свойства; Ki — важность i-го свойства продукта.
	Розенберга.	i — номер мотива; Xi - субъективная оценка пригодности продукта для удовлетворения i-го мотива; Кi - важность i-го мотива.

Если величина Y в модели Фишбейна характеризует оценку отношения к продукту как к совокупности его свойств, то в модели Розенберга — как к способности удовлетворять совокупность нужд потребителя в терминах чувства и мотивов.

Модель с дифференциацией

Мнения потребителей имеют тот или иной разброс. При применении модели с дифференциацией преследуется цель — уменьшить влияние или даже исключить из рассмотрения те свойства продукта, по оценкам важности которых имеется наименьшее совпадение мнений потребителей, поскольку расхождение потребителей в своих мнениях свидетельствует о неоднородности выборки потребителей и приводит к недостоверности результатов.

В итоге будет иметься оценка отношения с акцентом на те свойства, по отношению к которым потребители достаточно едины. Фактически разброс мнений потребителей относительно важности свойств означает их неоднородность и, следовательно, необходимость сегментации. Соответственно далее следует сначала провести сегментацию, а затем вновь обратиться к оценке отношения. В основу сегментации (см. подразд. 23.7) должны быть положены именно те свойства продукта, по которым имеется разброс оценок важности.

Степень согласованности мнений экспертов учитывается через дифференциацию i-го признака — Di. Дифференциация рассчитывается по формуле среднеквадратического отклонения оценки выраженности конкретного свойства различными респондентами:

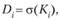
где Ki — важность свойства.

Для свойств, по которым мнения относительно их важности далеки друг от друга, дисперсия велика. Комплексная оценка отношения дается по следующей мультиатрибутивной модели:

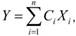
где i — номер свойства; Сi — характерность свойства; Xi — выраженность свойства, рассчитываемая как средняя по респондентам.

Характерность имеет вид.

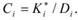
Здесь 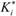- важность признака, рассчитываемая как средняя по респондентам. Фактически величина Ci представляет собой коэффициент вариации выраженности i-го свойства. В литературе встречаются и иные варианты построения модели с дифференциацией.

Десять замечаний по применению мультиатрибутивных моделей

Для облегчения практического применения моделей Фишбейна, Розенберга и модели с дифференциацией целесообразно рассмотреть несколько важных замечаний, которые относятся не только к этим моделям, а имеют более широкое применение.

Замечание 1. Компенсаторные оценки. Модели дают так называемую компенсаторную оценку, поскольку низкие оценки, но одним свойствам могут быть компенсированы высокими оценками по другим.

Замечание 2. Несколько респондентов. При применении моделей Фишбейна и Розенберга па основе использования результатов опроса не одного, а нескольких респондентов (j = 1, т) возникает задача последовательности осреднения и умножения. Формально возможны два альтернативных варианта — осреднение сомножителей или осреднение произведений в расчетной формуле. Следует применять первый вариант как более точный. Обоснование преимущества данного варианта основано на положениях теории вероятностей. При этом величины Kj и X в формулах (см. табл. 15.4) рассчитываются как средние значения по совокупности т респондентов (табл. 15.5).

Таблица 15.5

Расчет оценки отношения по результатам опроса т респондентов.

Средняя выраженность i-го свойства.	Средняя важность i-го свойства.	Модель.

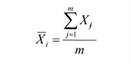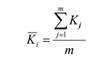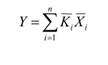Замечание 3. Таблицы для расчета. Если решается задача сравнения отношения к нескольким продуктам, то удобно применять расчетную табл. 15.6, обозначения в которой соответствуют единственному респонденту.

Замечание 4. Нормирование уровня комплексной оценки Y. Для наглядности оценки уровня Y по принципу «плохо — хорошо» целесообразно рассчитать уровень оценки.

Таблица 15.6

Расчетная таблица оценки отношения для нескольких продуктов

Свойство, i	Важность, X		Выраженность, К	КХ
	Продукт 1.	Продукт 2.		Продукт 1.	Продукт 2.
п
Итого.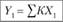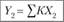

по отношению к максимальному уровню. Для этого можно вычислить максимальное значение комплексной оценки. Пусть К и X принимают значения 1, 2, 3 по принципу «чем больше, тем важнее» для К и «чем больше, темлучше» для X. Максимальная комплексная оценка 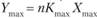, где п — число признаков-свойств. При одном признаке максимальная оценка равна 3•3 = 9, при двух — 2 • 9 = 18 и т. д. Для приведения оценки Y к нормированному виду ее следует разделить на 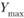. Тогда комплексная нормированная оценка принимает вид .

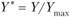Замечание 5. Нормирование весовых коэффициентов. Удобнее применять весовые коэффициенты в нормированном виде 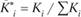. В результате достигается равенство единице суммы всех нормированных весов.

Замечание 6. Применение весовых коэффициентов для сгруппированных свойств. Пусть все п свойств разделены на L групп. Каждому свойству присваивается вес к в группе. Каждая группа имеет свой вес К по отношению к другим группам. В результате модель принимает вид.

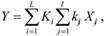
где L — число групп; l — число свойств в группе.

Возможно нормирование весов как внутри группы, когда сумма индивидуальных коэффициентов в каждой группе равна единице, так и среди групп. Сумма групповых весовых коэффициентов равна единице.

Замечание 7. Число градаций. Варианты по числу градаций могут быть самыми различными, начиная с двух градаций для важности и выраженности. Некоторые рекомендации относительно используемых шкал и последовательности оценивания переменных содержатся в литературе. Кроме пятибалльной иногда предлагается использовать семибалльную униполярную шкалу с градациями от 1 до 7 в виде 1−2-3−4-5−6-7. Для весовых коэффициентов или уровней значимости К соответственно применяется семиуровневая униполярная шкала, причем с градациями не только от 1 до 7, а также с градациями от 0 до 6 в виде 0−1-2−3-4−5-6.

Замечание 8. Согласование шкал. Наиболее типичным, но не единственным вариантом согласования шкал по К и по X является тот, когда обе эти величины отражают прямую зависимость в том смысле, что для величины К применяется правило «чем важнее, тем больше», а для величины X — «чем лучше, тем больше» .

Замечание 9. Предпосылка «чем лучше, тем больше». Модели основаны на предпосылке, что чем выше оценка выраженности свойства, тем лучше. Если это неочевидно, то целесообразно применять модель с идеальной точкой (см. подразд. 16.3), в которой реальный продукт сравнивается с идеальным продуктом по выраженности свойств.

Замечание 10. Оценки соответствия. Как правило, для оценки уровня выраженности в моделях Фишбейна и Розенберга применяются абсолютные оценки с вариантами интерпретации уровней «высота уровня» (от низкого до высокого) или «плохо — хорошо». Однако содержательно применение шкалы с интерпретацией уровней выраженности в виде соответствия запросам от полного несоответствия до полного соответствия (см. табл. 15.1). Полученные модели дают оценку соответствия продукта и результата его потребления ожиданиям потребителя. Модель Фишбейна дает оценку соответствия ожиданиям уровня потребительских свойств, а модель Розенберга — ожиданиям чувств и мотивов.