Объединенная модель против модели со случайными эффектами

Анализ дисперсии (тест Фишера)

Первый способ проверки отсутствия индивидуальных эффектов состоит в проверке нулевой гипотезы о равенстве нулю дисперсии Оц: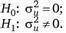

Этот тест легко выполняется если оценить внутригрупповую и межгрупповую дисперсии, из которых мы можно получить оценки дисперсии остатков. Во внутригрупповой модели дисперсия остатков ?2 будет равна ?2, а в межгрупповой модели дисперсия остатков составит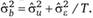

При выполнении предположения о нормальности величина.

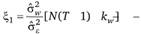(9.68).

будет иметь? -распределение с 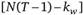степенями свободы, где kw — число регрессоров во внутригрупповой модели, и величина.

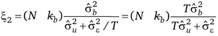(9.69).

будет иметь ?2-распределение с (JV-fcb) степенями свободы, где кь — число регрессоров в межгрупповой модели. Как следствие величина ?2 / ?] будет иметь F-распределение с (?-кь) и 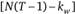степенями свободы.

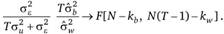(9.70).

Тогда при нулевой гипотезе, состоящей в том, что ?2 = 0, выражение (9.66) примет вид.

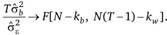(9.71).

В результате мы можем отклонить нулевую гипотезу и принять альтернативную в том случае, когда F-статистика (9.71) больше, чем Fкр со степенями свободы 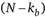и 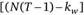для соответствующего уровня значимости. Получается, что если индивидуальная дисперсия межгрупповой регрессии, которая вычисляется по N наблюдениям, умноженная на Т, больше, чем остаточная дисперсия во внутригрупповой регрессии, то гипотеза об отсутствии индивидуальных эффектов отклоняется: такие эффекты присутствуют.

Проведем анализ дисперсий в модели индивидуальной заработной платы. Во внутригрупповой модели оценка дисперсии ошибок 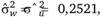а в межгрупповой модели оценка дисперсии ошибок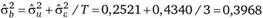

Для проверки нулевой гипотезы о равенстве нулю дисперсии ?" вычислим F-статистику.

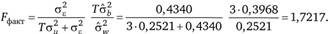
Критическое значение F-статистики для уровня значимости 0,05 составляет 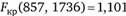. Так как вычисленное значение F-критерия больше критического значения 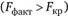, то мы можем отклонить нулевую гипотезу и принять альтернативную гипотезу о том, что дисперсия ?" не равна нулю. Таким образом, можно сделать вывод о присутствии индивидуальных эффектов и сделать выбор в пользу модели со случайными эффектами.

Тест множителей Лагранжа Бреуша — Пагана

Т. Бреуш и Э. Паган^[1] в 1980 г. предложили тест множителей Лагранжа, который может использоваться для тестирования модели со случайными эффектами против объединенной модели. При помощи этого теста проверяются следующие гипотезы:

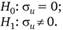
Из формулы (9.52) очевидно, что при справедливости нулевой гипотезыо равенстве дисперсии ?" нулю ковариационная матрица 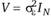, и в результате модель со случайными эффектами сокращается до объединенной МНК-регрессии с независимыми одинаково распределенными ошибками.

Проверка этой гипотезы основана на МНК-остатках eit из объединенной регрессии и требует вычисления LM-статистики При нулевой гипотезе LM-статистика будет асимптотически иметь ?2-распределение с одной степенью свободы. В результате, если LM-статистика, вычисленная на основе остатков МНК-регрессии, больше, чем 3,84 (при проверке гипотезы на 5%-ном уровне значимости), то нулевая гипотеза об отсутствии индивидуальных случайных эффектов отвергается и принимается альтернативная гипотеза об их присутствии. В противном случае у нас нет оснований для того, чтобы отвергнуть нулевую гипотезу.

LM-статистика для нашего примера, вычисленная по формуле (9.72) на основе МНК-остатков еи из объединенной регрессии, составила LM = 253,15, что намного больше критического значения ?2? с одной степенью свободы на 5%-ном уровне значимости, т. е. мы можем отклонить нулевую гипотезу о равенстве нулю лисперсии ?1(и принять альтернативную гипотезу о том, что дисперсия ?" не равна нулю. Таким образом, тест множителей Лагранжа Бреуша — Пагана свидетельствует о том, что в нашей модели присутствуют индивидуальные эффекты, и мы делаем выбор в пользу модели со случайными эффектами.

Тест Хонды

Недостаток теста Бреуша — Пагана состоит в том, что он представляет собой двусторонний тест, тогда как дисперсия должна быть либо нулевой, либо положительной. Для того чтобы охватить эту проблему, Ю. Хонда^[2] в 1985 г. предложил очень простой односторонний тест. Тест Хонды заключается в том, чтобы рассматривать квадратный корень LM-статистики Бреуша — Пагана. Тест показал, что при нулевой гипотезе об отсутствии индивидуальных эффектов, квадратный корень имеет нормальное распределение. Статистика Хонды определяется по формуле.

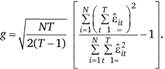
Если g-статистика Хонды больше, чем 1,64, то нулевая гипотеза об отсутствии индивидуальных эффектов отклоняется. Тест Хонды приводит к отклонению нулевой гипотезы гораздо чаще, чем это делает LM-статистика Бреуша — Пагана.

В нашем примере статистика Хонды g = 15,91 также свидетельствует о присутствии индивидуальных эффектов в модели и показывает, что модель со случайными эффектами больше подходит для наших данных, чем объединенная модель.

• [1] Breusch Т. S. and Pagan A. R. The Lagrange Multiplier Test and its Applications to Model Specification in Econometrics. Review of Economic Studies, Vol. 47 (1980). Pp. 239−253.
• [2] Honda Y. Testing the Error Components Model with Non-normal Disturbances. Review of Economic Studies. Vol. 52 (1985). Pp. 681−690.