Многофакторная модель. 
Корпоративные финансы

Альтернативой модели САРМ является многофакторная модель APT (arbitrage pricing theory), которую предложил в 1976 г. С. Росс. Эта модель опирается на предположение, что рынок находится в равновесии, если на нем невозможно совершение арбитражных сделок.

Арбитражем (arbitrage), или арбитражной сделкой, называется такая безрисковая сделка, которая позволяет ее инициатору получать прибыль. По сути, такие операции бывают двух видов:

• • инвестор может сформировать портфель активов, не затратив сейчас собственных средств, но по которому впоследствии получит положительный доход и отсутствие каких-либо обязательств перед третьими лицами;
• • инвестор сейчас может составить портфель с положительной текущей стоимостью (т.е. он получит доход от него прямо сейчас), по которому впоследствии не будет никаких обязательств перед третьими лицами.

В остальном подход к определению стоимости цены актива аналогичен подходу в модели САРМ. Авторы модели APT исходят из того факта, что цена актива определяется не только связью с рыночным портфелем, но и многими другими факторами, в основном макроэкономическими.

В любой момент времени основное уравнение модели может быть записано в виде.

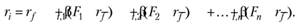(5.20а) В формуле (5.20а) 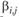показывает чувствительность доходности i-го актива к фактору, а 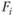- значение доходности некоторого индекса, связанного с фактором тогда 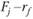показывает размер премии за риск по фактору j.

По сути, как модель САРМ связана с однофакторной линейной регрессией, так модель APT связана со множественной линейной регрессией:

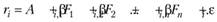(5.20б) Из формулы (5.20б) выводятся следующие соотношения. Чувствительность портфеля к фактору k равна средневзвешенной чувствительности к этому фактору всех активов, входящих в состав портфеля:

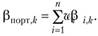(5.21а) Дисперсия остатков портфеля есть средневзвешенная сумма дисперсий остатков по каждому фактору (т.е. подразумевается, что ).

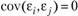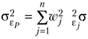(5.21б) В целом дисперсия портфеля может быть разложена на несколько составляющих, связанных с выделенными и со всеми остальными факторами:

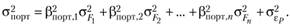(5.21в) Ковариация между любыми двумя активами может быть найдена из соотношения.

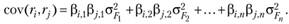(5.21г) Хотя по смыслу с точки зрения статистики (эконометрики) модель APT должна быть лучше модели САРМ, используется эта модель намного реже.

Связано это с тем, что сама модель не дает четких указаний ни на то, сколько факторов необходимо использовать для ее построения, ни на то, какие именно факторы необходимо учитывать. Это лишает возможности сравнить результаты модели APT, построенной разными аналитиками. Например, один аналитик может использовать в качестве факторов:

• • темп роста реального ВВП страны;
• • темп инфляции в стране;
• • реальную ставку процента внутри страны;
• • процентное изменение в реальных ценах на нефть;
• • темп роста сбережений граждан.

Пример 5.8. Предположим, что аналитик использует трехфакторную модель APT, а безрисковая ставка равна 5%. Вы создаете портфель из двух активов А и В в равных пропорциях. Данные по рынку и этим активам приведены в табл. 5.4.

Таблица 5.4

К примеру 5.8.

Фактор			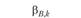Премия за риск по фактору, %.
	0,3.	0,5.
	0,2.	0.6.
	1,0.	0,7.

Основываясь на имеющихся данных, рассчитайте ожидаемую доходность создаваемого портфеля.

Решение

Для начала необходимо найти коэффициенты бета портфеля по каждому из факторов с помощью формулы (5.21а):

Теперь с помощью формулы (5.20а) находим ответ задачи:

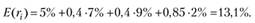
Таким образом, ожидаемая доходность формируемого портфеля составит 13,1%.

В заключение приведем еще несколько примеров с решениями, чтобы у читателя была возможность лучше разобраться в материале главы.

Пример 5.9. В двухпериодной экономике (в которой нет возможностей для коротких продаж) обращаются два актива со следующими характеристиками: ожидаемые доходности , стандартные отклонения доходностей 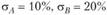, коэффициент корреляции между доходностями активов А и В равен нулю. Безрисковая ставка равна 5%. Известно, что инвестор имеет функцию полезности, которую можно выразить зависимостью

• 1. Определите состав и параметры портфеля GMV, составленного только из рисковых активов, имеющего минимальную дисперсию.
• 2. Определите состав и параметры портфеля Т, составленного только из рисковых активов, самого выгодного для инвесторов с точки зрения вознаграждения за риск.
• 3. Постройте линии CAL на основе портфеля GMV и на основе портфеля Т.
• 4. Определите оптимальный портфель для инвестора для двух полных портфелей из предыдущего пункта. К каким выводам приводит полученный результат?

Решение

1. Пусть 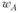- вес актива А в составе рискованного портфеля GMV. Тогда дисперсия доходности такого портфеля будет равна 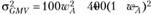, поскольку коэффициент корреляции между доходностями активов равен нулю. Таким образом, для ответа на первый вопрос задачи возникает необходимость решения задачи на нахождение безусловного экстремума вида.

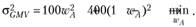
Решая эту задачу, получаем.

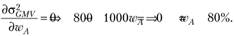
Таким образом, оптимальный состав рискового портфеля с минимальной возможной дисперсией доходности следующий: 80% вложений в актив А и 20% в актив В. А его параметры, соответственно, равны:

2. Лучший портфель для инвесторов с точки зрения вознаграждения за риск — это портфель Т, у которого наклон линии CAL, проведенной через него, будет максимальным. Пусть х — доля актива А в таком портфеле, тогда доходность портфеля будет , а дисперсия доходности портфеля будет 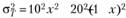-(так как корреляция равна нулю). Поэтому поиск портфеля с наибольшим тангенсом угла наклона линии CAL превращается в задачу поиска безусловного экстремума:

Используя правило дифференцирования.

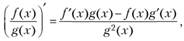
получаем уравнение 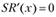, или, после некоторых математических преобразований,.

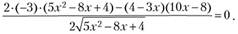
Решая это уравнение (приравниваем числитель к нулю, перемножаем и раскрываем скобки), получаем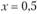

Таким образом, оптимальный состав рискового портфеля Т, самого выгодного с точки зрения вознаграждения за риск, следующий: 50% вложений в актив А и 50% - в актив В. А его параметры, соответственно, равны:

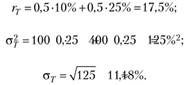
3. Уравнение линии распределения капитала выглядит как 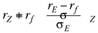, где Е — портфель, через который проходит линия распределения капитала. Поэтому:

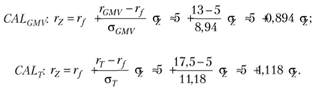
4. Так как мы знаем составы рискованных портфелей GMV и Т, то, подставляя в функцию полезности соответствующую линию распределения капитала, получим функцию полезности от одной переменной (от стандартного отклонения). Максимизируя функцию полезности в этом виде, находим стандартное отклонение оптимального для инвестора портфеля и уже по этому отклонению находим состав полного портфеля.

Для портфеля GMV:

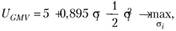
откуда 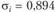. Поскольку для полного портфеля выполняется 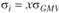•, где х — доля портфеля GMV в составе полного портфеля, имеем , откуда 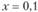. Другими словами, в этом случае для инвестора оптимальным будет портфель, состоящий из 10% GMV и 90% безрискового актива.

Для портфеля Т:

откуда 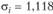. Поскольку для полного портфеля выполняется 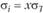•, где х — доля портфеля Т в составе полного портфеля, имеем 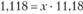, откуда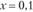

Другими словами, в этом случае для инвестора оптимальным будет полный портфель, состоящий на 10% из рискованного портфеля Т и на 90% из безрискового актива. Поскольку портфель Т состоит поровну из активов А и В, то оптимальный полный портфель для инвестора следующий: 5% вложений в актив А, 5% вложений в актив B, 90% вложений в безрисковый актив.

Данные результаты полностью соответствуют тому, что мы должны были получить. Это хорошо видно на графике (рис. 5.16).

Пример 5.10. Доходность ценной бумаги А на рынке страны за полные последние шесть лет была {5%; -1%; 12%; 2%; 0%; 7%}, а доходность ценной бумаги В, соответственно, следующей: {4%; 1%; 4%; 2%; 3%; 3%}. Каково наименьшее стандартное отклонение доходности портфеля, составленного из данных акций, с доходностью, равной 3,69%?

Рис. 5.16. К примеру 5.9.

Решение

Находим значения математического ожидания доходности обоих активов:

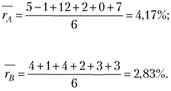
Пусть wA - доля актива А в портфеле, тогда должно выполняться равенство , так как для одной доходности существует только один портфель (вспомните, как выглядит допустимое множество портфелей для случая двух рискованных активов). Решая последнее уравнение, получаем 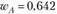Дальнейшие расчеты делаем в таблице (табл. 5.5).

К примеру 5.10.

Таблица 5.5.

Исход.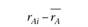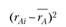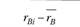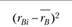
	5−4,17 = 0,83.	0,6889.	4 — 2,83 = 1,17.	1,3689.	0,9711.
	— 1 -4,17 = -5,17.	26,7289.	1 — 2,83 = -1,83.	3,3489.	9,4611.
	12−4,17 = 7,83.	61,3089.	4 — 2,83 = 1,17.	1,3689.	9,1611.
	2−4,17 = -2,17.	4,7089.	2 — 2,83 = -0,83.	0,6889.	1,8011.
	0−4,17 = -4,17.	17,3889.	3 — 2,83 = 0,17.	0,0289.	— 0,7089.
	7−4,17 = 2,83.	8,0089.	3 — 2,83 = 0,17.	0,0289.	0,4811.

Таким образом, 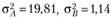и 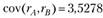. Теперь у нас есть вся информация для расчета дисперсии доходности портфеля, составленного из активов А и В:

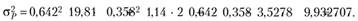
Следовательно,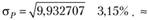

Пример 5.11. Эксперты оценили поведение двух ценных бумаг и одного фондового индекса в зависимости от результатов выборов президента (табл. 5.6). Доходность государственных долгосрочных облигаций, независимо от результатов выборов, составляет 1% годовых.

К вам пришел клиент, который желает вложить свои деньги в акции. На основе этих данных найдите: 1) дисперсии обеих акций и рынка; 2) коэффициенты «бета» обеих акций; 3) определите, какие акции переоценены, а какие недооценены; 4) дайте рекомендацию не склонному к риску инвестору относительно инвестиций в активы в составе портфеля и без портфеля.

Таблица 5.6

К примеру 5.11.

Решение

Используем метод расчетов как в примере 5.10 с поправкой на вероятности наступления исходов и получаем:

Теперь находим коэффициенты «бета»: 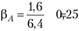и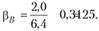

По модели САРМ находим доходности акций А и В: 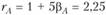и 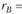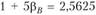. Отсюда очевидно, что обе акции являются недооцененными, поскольку текущие средние значения их доходностей (выступающие как их фактическая доходность) больше, чем доходности, посчитанные по модели. Для инвестора в состав портфеля посоветуем акцию А (у нее меньший коэффициент «бета»), а без портфеля — снова акцию А, так как у нес меньше стандартное отклонение. Хотя для отдельной акции можно применить коэффициент вариации, т. е. риск на единицу доходности:

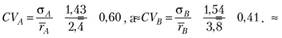
Поэтому в виде отдельной акции возможен выбор акции В как наименее рискованной в относительном плане, а не в абсолютном (более детальный выбор делается на основании функции полезности инвестора).

Пример 5.12. Предположим, что функция полезности инвестора имеет вид , где 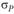 — стандартное отклонение доходности портфеля. Инвестор составляет портфель из акций А и В, про которые известно, что 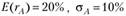, 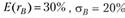. Коэффициент корреляции между доходностями равен . Необходимо определить, в каких пределах может быть ожидаемая доходность портфеля инвестора, в случае если он сформирует таковой из указанных активов.

Решение

В данной задаче решение сводится к нахождению условного экстремума функции полезности, или условной минимизации функции дисперсии портфеля инвестора, т. е.

при условии что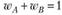

Расписывая формулу дисперсии портфеля из имеющихся двух активов и подставляя из условия выражение одного веса через другой, получаем задачу безусловной максимизации функции:

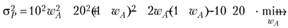
Выписываем условие первого порядка (первая производная равна нулю):

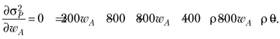Отсюда 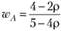и, соответственно,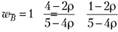

Подставляя эти оптимальные значения весов в формулу для расчета ожидаемой доходности портфеля, получаем:

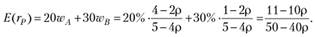
Это выражение является монотонно убывающей функцией относительно р и имеет минимальное значение 1/10 (10%), а максимальное 21/90 (23,33%).