Сюжет «Страшный дом на кладбище»

Еще одна динамическая игра с неполной информацией может быть сконструирована на основе сюжета про «виртуальное» посещение Алисой «страшного дома на кладбище» (гл. 10 литературного приложения).

Мы имеем трех участников. Во-первых, это Модест Эрастович Носфератов (игрок 1), которого Алиса относит к числу своих недоброжелателей. Во-вторых, это Природа (игрок 2). И наконец, сама Алиса (игрок 3).

В тот ненастный и роковой вечер, когда в Алисину голову пришла, скажем откровенно, нелучшая мысль следить за Носфератовым, у последнего было два выбора:

• • не предпринимать никаких действий и мирно ехать домой (на рис. 10.4 данная стратегия обозначена символом );
• • отправиться (с не вполне ясными целями) в дом па кладбище (на рис. 10.4 стратегия обозначена символом в ).

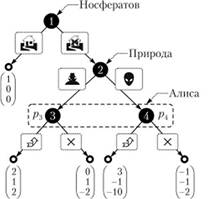
Рис. 10.4. Игра «Страшный дом на кладбище» .

Далее в игру вступает Природа, у которой есть две возможности:

• • создать Носфератова обычным человеком из крови и плоти, экстравагантным любителем ночных прогулок по нестандартным краеведческим маршрутам, что в общем-то не выглядит чем-то абсолютно невозможным (на рис. 10.4 стратегия обозначена символом ):
• • создать Носфератова сверхъестественным существом (вампиром, оборотнем либо еще какой-то нечистью, приравненной к ним в нравах, а самое главное, в возможностях), выбравшим в качестве очередной жертвы несчастную Маргариту (на рис. 10.4 эта стратегия обозначена символом ).

Последнее кажется практически невозможным, но, как любила повторять Маргарита, «а вдруг…» Самое неприятное для Алисы, что ход Природы по определению экзистенциального естества Носфератова иенаблюдаем для нее. А значит, информационное множество, из которого Алиса будет делать свой ход, будет неодноэлементным. Таким образом, ее выбор будет определяться се представлением о Носфератове: с вероятностью 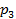он все-таки человек, с вероятностью = 1 — 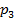— сверхъестественное существо (далее, но соображениям лаконичности изложения, — просто вампир).

Остановимся теперь на возможностях Алисы. Она стоит перед выбором: проникнуть в комнату и помочь подруге Рите (стратегия «вход», на рис. 10.4 обозначена символом 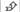) либо незаметно покинуть место действия и оставить подругу в руках злодея (стратегия «бегство», на рис. 10.4 обозначена как X).

Зададим (конечно, условно) значения платежей сторон для возможных ситуаций в рассматриваемой игре.

Если Модест Носфератов, как это и положено мирному и добропорядочному городскому жителю, проводит вечер дома (стратегия «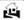 »), то игра закапчивается на первом шаге с результатом (+1) для него. Полезности Природы и Алисы, не получающих в этой ситуации возможности хоть как-нибудь проявить себя, мы с полным на то основанием можем считать равными 0 (нейтральными).

Теперь обсудим полезности участников в тех ситуациях, когда действие игры все-таки переносится ближе к кладбищу. Относительно Природы вполне разумным выглядит допущение, что ей не очень-то нравится плодить нечистую силу (в противном случае мы бы в повседневной жизни сталкивались с этой самой силой значительно чаще). Следовательно, Природа получает (+1), если создает Носфератова человеком, и (-1) — в противном случае.

Относительно полезностей Носфератова и Алисы будем считать следующее:

• • Алиса, войдя в дом (" 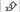"), при встрече с Носфератовым-человеком получает (+2), однако столкновение с Носфератовым-вампиром приводит к неприемлемому ущербу в (-10). При этом Носфератов, если он, конечно, человек, при встрече с Алисой получает (+2) — приятно познакомиться с умной и обаятельной девушкой, особенно когда ты ночью в одиночестве бродишь по кладбищу. Носфератов-вампир при встрече Алисой получает (+3) — одинокий вампир, встретивший ночью поблизости от кладбища умную и обаятельную девушку, будет обрадован даже больше, чем простой смертный.
• • В случае если Алиса не решается войти в комнату («´»), она за бесславное бегство с поля боя получает (-2), Носфератов-человек имеет нулевую полезность (не стоит расстраиваться, если ты, бродя ночью в одиночестве по кладбищу, никого там не встретил), Носфератов-вампир получает полезность в размере (-1) (так сказать, «обломись, нечистая сила»).

Совершенное равновесие, но Байесу — Нэшу в данной игре находится несложно:

• • « «— Носфератов отправляется на прогулку в район страшного дома на кладбище (2 > 1);
• • « «— Природа создает Носфератова человеком (1>-0);
• • « >» — Алиса заходит в комнату и знакомится с господином Носфсратовым в его человеческой ипостаси (2 > -2);
• • при этом Алиса руководствуется представлением: Носфератов — человек с вероятностью р₃ = 1 и вампир с вероятностью р₄ = 0.

Данные действия являются последовательно рациональными, а представления единственного игрока (Алисы), совершающего ход из неодноэлементного информационного множества, согласованы с ходами, задаваемыми равновесными стратегиями игроков.

Авторы заранее готовы признать справедливость острых критических замечаний со стороны серьезных и обстоятельных читателей в адрес построенной модели. Безусловно, можно усомниться в том, что удовольствие Носфератова-человека от ночного рандеву на кладбище (+2), а от вечера у уютного домашнего очага — всего лишь (+1). Но в то же время мы не сомневаемся (в контексте рассказываемой истории!), что если он отправляется на кладбище, то точно встречается там с Алисой. Столь фантастический и гротескный сюжет был выбран вполне сознательно. Он позволяет достаточно ярко отразить значение требований, содержащихся в условии R4.

Рассмотрим ситуацию, при которой М. Э. Носфератов едет домой, т. е. игры как таковой не происходит. При этом другие участники просто не получают права хода, а значит, их стратегии по существу не работают. Однако при формальном определении ситуации равновесия мы должны описать стратегии всех игроков. Покажем, к чему это может привести.

Информационное множество игрока 3 (Алисы), состоящее из вершин 3 и 4, не достигается, т. е. условия R1 — R3 на него не распространяются. В таком случае, если Алиса посчитает, что Носфератов — вампир (сформирует представления р₃ = 0 и р₄ = 1), ей следует выбирать ход «´», так как -2 >-10. Следовательно, если бы мы руководствовались только условиями R1 — RЗ, то под определение равновесия «подпадала» логически абсурдная ситуация:

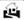• • « «— Носфератов отправляется домой (1 > -1);
• • « «— Природа создает Носфератова человеком (1 > -1);
• • «´» —Алиса не заходит в комнату (-2 > -10), потому что считает его вампиром (р₄ = 1).

Условие R4, требующее (по возможности) соответствия представлений игроков в информационных множествах, лежащих вне равновесного пути, правилу Байесу и выбранным ими равновесным стратегиям, исключает подобные ситуации. Действительно, представление Алисы о Носфератове как о вампире противоречит предшествующему ходу Природы, которая может в равновесии создать его исключительно человеком: . Именно поэтому авторы позволили своей героине как девушке современной и обладающей хорошим экономико-математическим образованием иметь подобные представления исключительно во сне.

Существенность «роли» условия R4 в процедурах отсечения «неосмысленного» равновесия для данной игры проявляется еще и в том, что в ней нет под-игр (в силу специфической структуры информационных множеств), а значит, в отличие от динамических игр с полной информацией, не могут быть применены и критерии «совершенства равновесия в под-играх» .

Ранее мы уже отмечали, что теоретико-игровые концепции равновесия имеют не только математическое, но и мировоззренческое значение. Например, когда мы упрекаем коголибо в «неадекватном поведении», это по существу и есть отражение того факта, что данный человек неверно представляет реальное положение (информационное множество), в котором он оказался в результате развития предшествующих событий, а следовательно, принимает неверные решения о своих последующих действиях.

* * *.

В заключение вернемся к игре, построенной на основе сюжета «Первый визит к Нау.Ру» (см. рис. 10.1), и определимся с тем, какие ситуации являются совершенным равновесием по Байесу — Нэшу в ней.

В первую очередь отметим, что если Алиса имеет априорное представление, что тип Нау.Ру Good (p_G = 1, р_B = 0), то ей следует играть стратегию (A, F), а Нау.Ру — стратегию (Н, Н).

В то же время, если Алиса имеет априорное представление, что тип Нау.Ру Bad (p_G = 0, р_B = 1), то ей следует играть стратегию (NA, NF), а Нау.Ру — стратегию (Н, Н).

В случае, когда представления Алисы о типах Нау.Ру таковы, что 0 < p_G < 1 и 0 < p_B < 1, то, с учетом того что Нау.Ру всегда выгоднее играть Help, она в информационном множестве V₂ должна иметь представления.

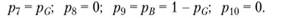
Из этого следует, что выбор Алисы между стратегиями A (ask) и NA (по ask) должен происходить па основе ее ожидаемых полезностей в ситуациях, заканчивающихся тем, что она прислушивается к совету Нау.Ру (F). Они, соответственно, равны:

• • 2• p_G для хода из вершины 7 (если тип Нау.Ру реализовался как Good);
• • -3• (1- p_G) для хода из вершины 9 (если тип Нау.Ру реализовался как Bad).

Сравнивая ожидаемую полезность 2• p_G — 3(1 — p_G) с полезностью 0, которую получит Алиса, играя NA, получаем условия совершенного байесова равновесия:

• • при представлениях Алисы с p_G ³ 3/5 ей следует играть стратегию (A, F), а Нау.Ру — стратегию (Н, Н);
• • при представлениях Алисы, в которых p_G? 3/5 (р_B ³ 2/5), ей следует играть стратегию (NA, NF), а Нау.Ру — стратегию (Н, Н).

Как мы помним, по факту Алиса выбрала NA. Видимо, ее представления о научном руководителе были недостаточно хороши.

Данный пример не должен порождать иллюзий относительно простоты процедур нахождения совершенных байесовых равновесий. В общем случае требования о согласованности равновесных стратегий и представлений игроков, а также отсутствие под-игр приводят к необходимости решать достаточно сложные системы уравнений и неравенств.