Методы спуска. 
Приближенное решение задач выпуклого программирования градиентным методом

Общая схема решения задач математического программирования методами спуска состоит в построении последовательности.

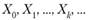(10.14).

решений системы ограничений данной задачи по следующему принципу: в качестве 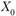выбирается, вообще говоря, любая точка области решений и затем каждая последующая точка получается из предыдущей по формуле.

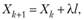(10.15).

где 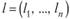 — некоторое направление (т.е. вектор),.

а? — число. При этом направление? и «длина шага»? выбираются так, чтобы обеспечить сходимость последовательности (10.14) к оптимальному решению . В общем случае процесс получения последовательных приближений Хк бесконечен (и тогда некоторое 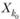берется за приближенное значение оптимального решения X*), однако иногда процесс может завершиться и за конечное число шагов, приводя к локальному, а в задачах ВП и глобальному оптимуму.

Находя производную по направлению 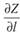, мы можем определять, является ли направление? «невыгодным» или «выгодным» в смысле приближения к оптимуму.

10.6. В задаче ВП нужно найти минимум функции.

при ограничениях: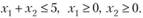

Взяв за Х0 точку (1; 1), проверить, приблизимся ли мы контимуму по направлению: а)? = (2; 1); б) /, = (-2; 1).

Решение. По критерию Сильвестра (10.5) нетрудно убедиться, что функция ? является выпуклой при .г, > 0,.

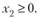Находим 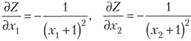, значит,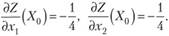

Отсюда, учитывая, что, по формуле (10.1) по лучаем:

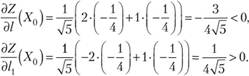
Таким образом, в направлении? функция Z убывает, и по этому направлению мы приближаемся к оптимуму, а в направлении /, функция возрастает, т. е. мы удаляемся от оптимума. >

Так как направление градиента VZ целевой функции является направлением ее наискорейшего роста, то при отыскании максимума вогнутой функции (минимума выпуклой функции) в качестве? часто берется VZ (-VZ) и тогда формула (10.15) принимает вид.

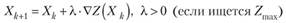(10.16).

ил и.

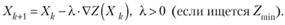(10.16').

Методы спуска, в которых итерационная последовательность (10.14) находится по формуле (10.16) (или (10.16')), называются градиентными. Друг от друга они отличаются способами выбора длины шага? и алгоритмами нахождения точки Хк+1, если Хк находится на границе области решений и формула (10.16) выводит Хкн за пределы этой области. Выбор длины шага? очень важен. Как видно из рис. 10.6, перемещаясь из точки Х0 в направлении VZ, мы в некоторый момент можем «проскочить» мимо точки Л', в которой достигается искомый максимум. Если величина? выбирается так, чтобы приращение функции VZ при перемещении из точки Хк в точку Хк+1 было наибольшим (при отыскании Zma! i) или наименьшим (при отыскании ??), то градиентный метод называется методом скорейшего спуска. Таким образом, по методу скорейшего спуска длина шага? в формуле (10.16) (или (10.16') выбирается так, чтобы при этом? достигался экстремум функции.

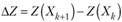. Обратите внимание на то, что при нахождении точки Хк+{ предыдущая точка Хк считается уже известной, т. е. Z (XA) и kZ (Xk) являются постоянными величинами, a VZ — функцией одной переменной ?. Продифференцировав функцию ?? с учетом выражения Хк+1.

по формуле (10.16)и выражения градиента в точке ,.

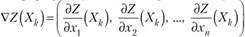, получим, что необходимое условие экстремума 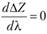примет вид.

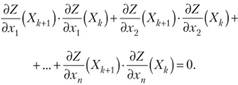(10.17).

Ему можно придать более компактную форму, если использовать скалярное произведение векторов:

• src="/imag/econom/krem_islopek/image1043.jpg" >(10.17')
• (Напомним, что скалярное произведение векторов в прямоугольной системе координат равно сумме произведений их соответствующих координат. Например, если? = (2,-1) и /, = (3, 5), то? • /j = 2 • 3 + (-1) •5 = 1. Скалярное произведение векторов равно нулю тогда и только тогда, когда они ортогональны.)

Если оптимум достигается внутри области решений системы ограничений данной задачи ВП, то нет опасности, что точка Хк+х, найденная по формуле (10.16) или (10.16'), выйдет за пределы этой области, и длину шага? определяем по формуле (10.17) без каких-либо дополнительных ограничений. Рассмотрим примеры решения таких задач, а к случаю, когда оптимум достигается на границе области, обратимся позднее. Вместо VZ (X0), VZ (Z,) и т. д. будем писать VZ (), VZ]t … Заметим также, что для различных к длина шага? по формуле (10.16), вообще говоря, различна и для строгости нужно было бы писать ??, но это сделало бы запись решения более громоздкой.

10.7. Используя метод скорейшего спуска, найти максимум функции при ограничениях:

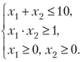
Решение. Функция (-?) является выпуклой при любых ?? х2 (проверьте это самостоятельно, см. (10.4) и задачу 10.2), значит, по свойству 1 выпуклых функций ? — вогнутая функция и поэтому се локальный максимум совпадает с глобальным. Область решений системы ограничений данной задачи изображена на рис. 10.6 (хотя, вообще говоря, ее построение для решения задачи необязательно).

В качестве исходной точки возьмем точку Х,(1; 2). Найдем частные производные функции ?:

Запишем общее выражение градиента:

(10.18).

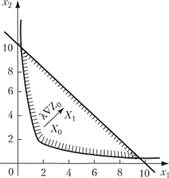
Рис. 10.6.

Подставляя в (10.18) координаты точки Х0, получим VZp=(6;6). По формуле (10.16) X, = Х0 + ??? = (1; 2)+ +?(6; 6) = (? + 6?; 2 + 6?). Подставляя координаты точки X, в (10.18), получаем.

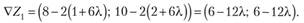
Теперь можем записать уоавнение (10.17') для нахождения 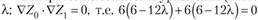, откуда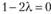

т.е. 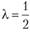. Подставив это значение в выражения X, и VZ, через? (см. выше), получаем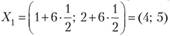

и 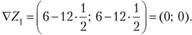Так как градиент в точ ке (4; 5) равен нулю, то X, является точкой максимума, Zmajt = 5. (За один шаг мы достигли точного оптимума. Это не является общей закономерностью; есть задачи, в которых оптимальное решение получается за большее число шагов, и задачи, в которых за любое конечное число шагов мы получаем лишь приближенное решение.) >

Для случая функции двух переменных метод скорейшего спуска имеет простую геометрическую интерпретацию: для любого к луч, идущий от точки Хк к точке Х/;+), перпендикулярен к линии уровня функции Z, проходящей через точку Хк (так как направлен по градиенту), и касается линии уровня, проходящей через точку Хк+{ (так как ввиду условия (10.16') он перпендикулярен к следующему лучу, который в свою очередь перпендикулярен к этой линии уровня). Таким образом, па плоскости скорейший спуск происходит по двум взаимно перпендикулярным направлениям так, как показано на рис. 10.7.

Замечание. Для упрощения счета можно в формулах (10.16) и (10.17') брать вместо XZk любой вектор с тем же направлением, т. е. координаты XZk можно умножать или делить на положительное число.

10.8. Найти методом скорейшего спуска с точностью до 0,01 минимум функции 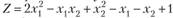при ограничениях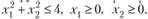

Решение. Найдем частные производные.

и общее выражение градиента целевой функции:

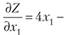
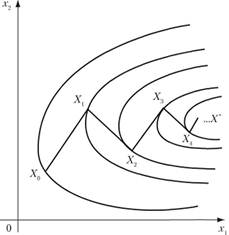
Рис. 10.7.

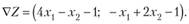
В качестве исходной берем точку (1; 1), которая лежит в области решений. Так как Z является выпуклой функцией, то для нахождения точек Хк, будем пользоваться формулой (10.16'), в которой, возможно, вместо VZ/; будем брать вектор 1к с тем же направлением, но более простыми координатами (см. замечание). Длина шага? находится по формуле (10.17'), на каждом шаге производятся аналогичные вычисления, которые подробно объяснены в предыдущем примере.

I шаг.

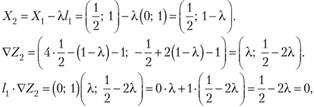
II шаг. Вместо VZ, возьмем /, =(0; 1). Тогда.

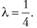
откуда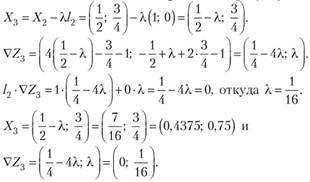

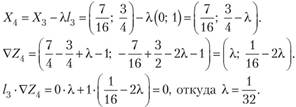
III шаг. Вместо VZ2 возьмем /2 = (1; 0). Тогда.

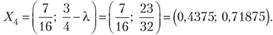
IV шаг. Берем /3 = (0; 1). Тогда

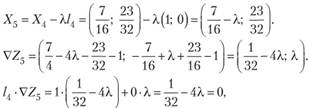
V шаг. Берем . Тогда.

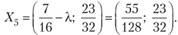
откуда и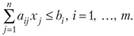

Таким образом, Х5 =(0,4 296 875; 0,71 875). Сравнение X4 и X- показывает, что координаты этих точек отличаются меньше чем на 0,01, и поэтому («правда, не совсем строго) можно положить А» (0,43; 0,72). Нетрудно убедиться, что все точки 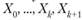лежат в области решений системы ограничений. >

Рассмотрим теперь задачу ВП, когда оптимум целевой функции достигается на границе области решений системы ограничений. В этом случае, взяв, как и ранее, в качестве исходной точки Х0 любую точку из области решений и находя последующие точки по формуле (10.16) или (10.16'), мы на некотором шаге получим, что Хк уже не лежит в области решений (рис. 10.8, а). Тогда вместо Хк берем точку Х'к, которая лежит на пересечении направления спуска с границей области решений, а последующие точки находятся путем проецирования на эту границу точек, получаемых обычным методом скорейшего спуска. Поскольку общий оператор проецирования не изучается в нашем курсе, ограничимся случаем, когда система ограничений линейная, т. е. область решений задачи для случая двух переменных ограничена отрезками прямых (рис. 10.8, б).

В этом случае система ограничений данной задачи примет вид.

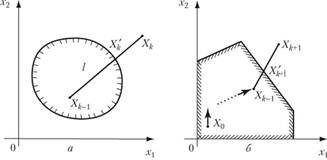(10.19).

Пусть по методу скорейшего спуска мы построили точки и убедились (подставляя в (10.19) координаты.

Рис. 10.8.

этих точек), что 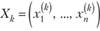лежат в области решений, а точка Xk+i уже не лежит в ней. Значит, координаты точки Х1/+{ не удовлетворяют хотя бы одному неравенству системы (10.19), например неравенству 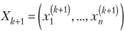(здесь i — номер конкретного неравенства). Пусть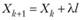 и 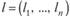, т. е.

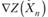(10.20)

Здесь 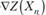 — направление спуска, которое совпадает с направлением при отыскании максимума или с направлением — 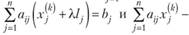при отыскании минимума.

Чтобы остаться в пределах области решений, следует вместо точки Х.+. взять точку, лежащую на том же направлении спуска, т. е. с координатами, удовлетворяющими условию (10.20), но с меньшей длиной шага ?. Значение? нужно выбирать так, чтобы точка оказалась на границе области решений, т. е. чтобы выполнялось равенство 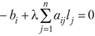Учитывая (10.20), получаем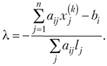 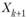. Отсюда.

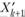(10.21).

Формула (10.21) дает значение ?, при котором направление спуска пересекает границу области решений. Если координаты точки 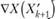нс удовлетворяют нескольким неравенствам системы (10.19), то нужно найти? по формуле (10.21) для каждого из этих неравенств и взять наименьшее из найденных значений. Подставляя его в (10.20), найдем координаты точки 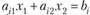, которая будет исходной для следующего шага решения. Так как проекция градиента 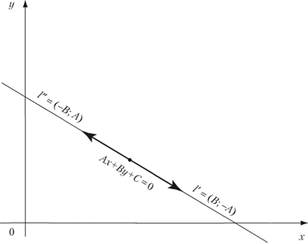задачи с линейными ограничениями лежит на границе области решений, а для случая двух переменных просто на прямой ,.

то направление спуска? на следующем шаге берется на этой.

Рис. 10.9.

границе. Оптимум достигается в той точке, в которой градиент перпендикулярен границе области решений.

Замечание. Если прямая на плоскости имеет уравнение 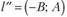, то ее направление задается вектором 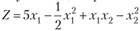или вектором 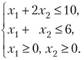(рис. 10.9).

10.9. Используя методскорейшего спуска, найти максимум функции при ограничениях:

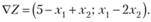
Решение. Отметим, что функция Z вогнутая, т. е. данная задача является задачей ВП. Находим частные производные 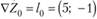функции Z и записываем общее выражение ее градиента:

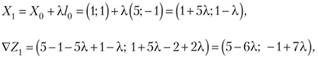
I шаг. В качестве исходной возьмем точку Х0 = (1; 1) (ее координаты удовлетворяют системе ограничений). Далее, используя формулы (10.15) и (10.16'), также, как и в задачах 10.6 и 10.7, находим точку Ху? . Тогда

Рис. 10.10.

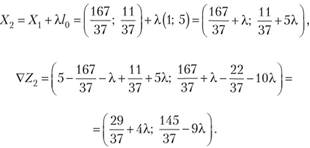
Отсюда? = -, т. е. 37?(4,5; 0,3). Так как 4,5 + 0,6<10 и 4,5+0,3<6, то X, находится внутри области ношений Хннс.^Ш.ШЛ, .,.

II шаг. Находим 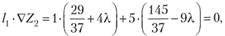. Мож, но не производить этих вычислений. Достаточно убедиться, что первая компонента положительна, и тогда взять /[ = (l; 5). В самом деле, 1^ 1/0, так как /, • /0 = 1 • 5 + 5 • (-1) = 0, и /, имеет то же направление, что VZr Теперь.

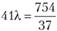
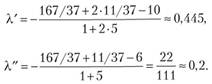откуда ,.

т.е.? ? 0,50 и Х2 ? (5,01; 2,78). Мы видим, что Х2 лежит уже вне области решений, причем не выполняются первое и второе неравенства. По формуле (10.21) находим? для обоих неравенств:

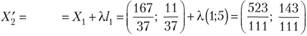
Берем и теперь получаем.

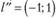
Нетрудно убедиться, что эта точка лежит на границе области X, + х2 = 16.

III шаг. Попав на границу области, мы должны двигаться по ней в сторону увеличения функции Z. Ввиду замечания, сделанного перед этим примером, направление прямой х,+.г2 = 16 задается вектором /'= (1; -1) или /" = (-1; 1). По формуле (10.1) находим производную функции Z по направлению Г в точке X.;.

Значит, в этом направлении функция Z убывает, и в качестве направления спуска следует взять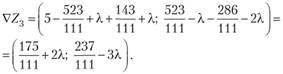

Итак,.

Далее поступаем, как и на предыдущих шагах:

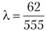
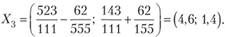
Отсюда 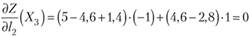и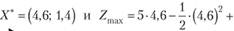

Так как (4,6 + 2,8) < 10, то точка Х3 является решением данной задачи.

Поскольку 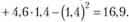, проекция градиента на это направление равна нулю, значит, мы достигли оптимального значения функции при данных ограничениях.

Таким образом,.