Непрерывные характеристики продолжительности жизни

Функция дожития

Классические таблицы смертности отражают значения показателей с интервалом, равным одному году. Однако на практике люди редко умирают в день своего рождения. Процесс вымирания совокупности людей является непрерывным.

В теории вероятностей^[1] стохастическую природу любой случайной величины X описывают функцией распределения F (x). Она определяется как вероятность того, что случайная величина X примет значение, меньшее х.

(7.13).

В демографической статистике F (x) называется функцией распределения продолжительности предстоящей жизни (lifetime distribution) и соответствует вероятности того, что новорожденный умрет до достижения возраста х лет.

В актуарной математике принято работать с дополнительной функцией распределения:

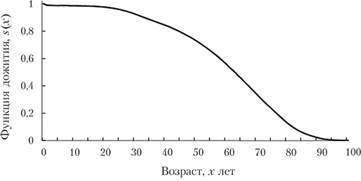
Рис. 7.1. График функции дожития s (x)

которая показывает вероятность того, что случайная величина X не меньше, чем некоторое число х. Применительно к продолжительности жизни, s (x) = 1 — F (x) — это безусловная вероятность того, что человек (новорожденный) доживет до возраста х лет. Функция ,?(.?) называется функцией дожития (выживания) {survival function):

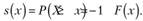(7.15).

Свойства функции дожития:

• 1) s (x) — функция убывающая;
• 2) функция s (x) непрерывна справа;
• 3) 5(+00) = 0;
• 4) 5(0) = 1.

Функция дожития является строго убывающей. В противном случае существовал бы фиксированный неслучайный период в жизни людей, когда смерть невозможна.

Функция дожития непрерывна, так как в противном случае существовал бы некоторый фиксированный момент в жизни человека, в который он умирал бы с положительной вероятностью. Это замечание приводит к тому, что функцию дожития можно было бы определить и как Р (Х >х) (понимая под функцией распределения Р (Х<�х)).

Так, в таблицах смертности обычно считают, что существует некоторый предельный возраст? (как правило,? = = ЮО-г-120 лет) и соответственно s (.r) = 0 при х> ?. В то время как при описании смертности аналитическими законами обычно считают, что время жизни неограниченно. Однако при этом подбирают вид и параметры законов так, чтобы вероятность жизни свыше некоторого возраста была бы пренебрежимо мала.

Функция дожития s (x) описывает среднюю долю живых представителей некоторой фиксированной группы новорожденных к моменту х.

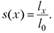(7.16).

Другими словами, из 100 000 рожденных в 2009 г. в России мальчиков до 30-летнего возраста доживут 94 344 человека (приложение 9).

Обозначим Т — продолжительность жизни новорожденного, а Тх как остаточную продолжительность жизни — время, которое проживет еще человек, достигнув возраста х. Тогда функция дожития примет вид.

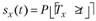(7.17).

и будет обозначать условную вероятность того, что человек возраста х лет, доживет до (х + I.) лет:

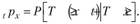(7.18).

Тогда:

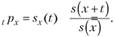(7.19).

Условная вероятность того, что человек возраста х лет умрет в промежутке от х до (х + t) лет определяется по формуле.

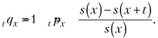(7.20).

Условная функция дожития sx(t) описывает среднюю долю живых возраста (х + t) лет из группы лиц, доживших до возраста х лет:

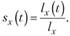(7.21).

Кривая смертей

Введем новую случайную величину , DX, как число умерших в возрасте от х до (х + t) лет из фиксированного числа /0 новорожденных. Она связана с величиной L (x), выражающей число живых представителей группы новорожденных /0 к моменту х, соотношением.

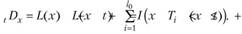(7.22).

Математическое ожидание случайной величины , т. е. среднее число представителей группы, умерших в возрасте от х до (х + t) лет, обозначается :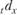

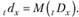(7.23).

Используя формулу (7.22), получаем:

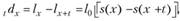(7.24).

где  — вероятность смерти в промежутке (х, х + t).

В актуарной математике часто встречается ситуация? = 1 год. В этом случае индекс I, указывающий на то, что рассматриваемая величина относится к периоду 1 год, опускается:

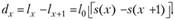(7.25).

Тогда вероятность смерти в промежутке (x, х + 1):

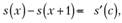(7.26).

где с — некоторое число между возрастом х и (х + 1).

Так как s '(х) мало меняется на протяжении одного года, можно считать, что верно приближенное равенство.

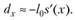(7.27).

Величина.

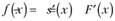(7.28).

называется в теории вероятностей плотностью случайной величины X с функцией распределения F (.г). Она описывает в актуарных расчетах долю умерших в возрастном интервале (х, х + 1) из исходной группы /0 новорожденных. При малых значениях п величина -s х) t приближенно описывает долю умерших в возрасте от х до (х + t) лет из исходной группы /0 новорожденных. В актуарной математике (рафик плотности /(.г) (или график IqJ (x)) называют кривой смертей (the curve of deaths).

Поскольку функция выживания л (.г) убывает, то плотность /(.г) = -s'(x) — неотрицательна, т. е. f (x) > 0.

Кроме того, из свойств функции дожития справедливы соотношения:

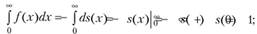(7.29).

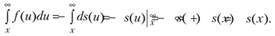(7.30).

Эти свойства являются характеристическими свойствами кривой смертей, т. е. если некоторая кривая обладает этими свойствами, то она является кривой смертей и может быть использована в качестве первичной характеристики продолжительности жизни.

• [1] Вентцель E. С. Указ. соч.