Вывод формулы оптимального размера заказа

Выводимая ниже формула, известная как формула Харриса (а также Маршака, Эрроу, модель Андлера и др.), получена впервые в 1915 г., хотя она и сейчас не потеряла своего значения.

Предположим, что спрос некоторого предприятия на определенный товар оценивается в 10 000 шт. в год. Хранение 1 шт. в течение года стоит 2,5 ден. ед., а каждый заказ (независимо от размера) — 500 ден. ед. Если бы мы сразу завезли весь товар на склад и постепенно отпускали бы его в производство, то затраты по хранению были бы относительно велики. Можно было бы сказать, что в среднем 5000 шт. пролежали целый год на складе (рис. 5.8). Тогда затраты на хранение составили бы 12 500, затраты на заказывание — 500, а всего — 13 000 ден. ед.

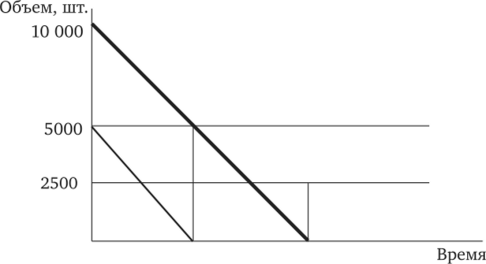
Рис. 5.8. График изменения товарных запасов при условии равномерного потребления.

Если бы общая потребность предприятия была бы разделена на два заказа, то средний уровень запаса, а вместе с ним и затраты были бы ниже, но зато само заказывание стоило бы дороже. В результате получилось бы: 2,5 • 2500 + 500 • 2 = 7250 ден. ед.

При дальнейшем дроблении заказа расходы на хранение продолжали бы снижаться, а на заказывание — расти. При этом общие расходы сначала бы снижались, а начиная с некоторого числа заказов, начали бы расти. Таким образом, возникает необходимость определить, как часто нужно заказывать, или, что-то же самое, каков должен быть размер заказа.

Сформулируем еще раз условия задачи.

• 1. Надо определить, чему должен быть равен размер заказа q.
• 2. Потребность в заказываемом продукте на плановый период известна. Q — потребность в течение периода.
• 3. Продукт потребляется равномерно.
• 4. Заказывать можно в любое время и любое количество.
• 5. На рассматриваемый процесс влияют следующие затраты:
  • а) расходы на заказывание (Z) пропорциональны числу заказов;
  • б) расходы на хранение (р) зависят от количества хранимого продукта и от уровня затрат на единицу хранимого продукта за период.
• 6. Целью является минимизация совокупных затрат на хранение и заказ (К).

Решение этой проблемы оказывается несложным, если целевую функцию сформулировать так, чтобы затраты в явном виде зависели от q.

Число заказов — Q / q (шт.). Тогда.

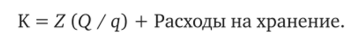
Расходы на хранение равны l/2qp.

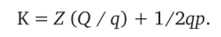
Для того чтобы найти минимум этой функции, надо взять первую производную и приравнять ее к 0.

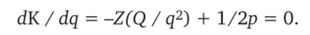
Эта формула называется формулой Харриса:

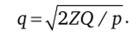
Пример. Пусть Q = 10 000 шт.; р = 2,5 руб./шт. в год; Z = = 500 руб./заказ.

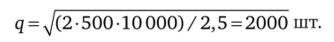
Может сложиться впечатление, что, несмотря на важность получаемого результата, эта формула не может широко использоваться на практике из-за ее предельной упрощенности: в жизни на принимаемое решение оказывает влияние значительно больше параметров, чем их фигурирует в модели.

Между тем такой вывод был бы ошибочным. Формула — это схема, которую можно наполнить самым разным содержанием.

Рассмотрим, например, задачу: определить оптимальный размер заказа, если месячная потребность в материале составляет 60 000 тыс. руб., стоимость одной доставки — 375 000 руб., а среднемесячные издержки, связанные с хранением товара, — 200 руб. на каждые 1000 руб. хранимого товара.

Очевидно, перед нами классическая иллюстрация применения формулы Харриса. Подставляя в формулу указанные величины, получаем: q = 15 000 тыс. руб.

Однако к этой же формуле может привести и задача в совсем другой постановке.

Предполагается открыть магазин. Он будет находиться в арендуемом помещении. Арендная плата составляет 240 000 руб. в год за 1 м². Арендуемая площадь включает площадь под склад, которая, исходя из предполагаемого ассортимента, должна определяться из расчета 1 м² для хранения товара стоимостью 250 000 руб. Завоз товара в магазин может осуществляться от одного до шести раз в месяц через равные промежутки времени. Стоимость доставки любой партии товара 375 000 руб. Затраты на хранение товара составляют 7%, а потери при хранении — 2% от средней стоимости хранимого товара в месяц. Среднемесячный объем закупки товара магазином ожидается на уровне 60 000 тыс. руб. в месяц. Кредит может быть получен под 36% годовых.

Требуется определить, какова арендуемая под склад площадь.

Здесь решение уже не столь очевидно, поскольку издержки, связанные с хранением, включают целый ряд составляющих.

Решим эту задачу. Для этого определим величину издержек, зависящих от размера хранимой партии товара, т. е. от размера заказа.

• 1. Арендная плата. 240 тыс. руб. в год делим на 12 мес. и получаем 20 тыс. руб. в мес.
• 20 тыс. — это арендная плата за 1 м². Поскольку 1 м² используется для хранения товара стоимостью 250 тыс. руб., то для хранения товара стоимостью 1 тыс. руб. надо: 20 тыс. руб. / 250 = 80 руб.
• 2. Затраты на хранение равны 7% от стоимости хранимого товара, т. е. 70 руб. для хранения товара стоимостью 1 тыс. руб.
• 3. Потери при хранении составляют 2%, т. е. 20 руб. на 1 тыс. руб. товара.
• 4. Хранение товара стоимостью 1 тыс. руб. в течение месяца ведет к необходимости выплаты в виде процентов за кредит 3% от этой стоимости (36% годовых разделить на 12 мес.), т. е. 30 руб.
• 5. Итого расходы, связанные с хранением товара стоимостью 1 тыс. руб.: р = 80 + 70 + 20 + 30 = 200 руб.

Далее задача решается по той же самой формуле, что и предыдущая. В результате получается тот же самый оптимальный размер заказа. Теперь на основании этого заказа определяется арендуемая площадь, которая оказывается равной 48 м².

Таким образом, получаем вывод 1: каждый параметр в формуле является результирующим целого ряда составляющих.

Едва ли кто-нибудь заметил, что предыдущую задачу мы решили неверно. Чтобы убедиться в этом, решим ее без использования формулы, так называемым прямым счетом. Все расчеты выполним в табл. 5.1.

Таблица 5.1

Затраты предприятия при разном количестве заказов в месяц.

В табл. 5.1 арендуемая площадь определена путем деления максимальной стоимости хранимого товара при каждом числе заказов (а это как раз и есть размер заказа) на норматив потребности в площади для хранения.

Например, для двух заказов в месяц: 30 000 тыс. руб. / 250 тыс. = = 120 м².

Затраты на хранение, потери и проценты за кредит определены как 7, 2 и 3% соответственно от средней стоимости хранимого товара. Стоимость заказа и доставки определяется путем умножения стоимости одного заказа и доставки на число заказов. Для двух заказов: 375 тыс. руб. • 2 = 750 тыс. руб.

Наконец, последняя строка является суммой строк 3, 5, 6, 7, 8.

В итоге получили результат, отличающийся от полученного по формуле: там оптимальным было заказывать четыре раза в месяц, здесь же минимальные затраты получаются при пяти заказах (наименьшее значение затрат в последней строке таблицы).

Упражнение 5.8.

Не заглядывая дальше, попытайтесь разобраться, где и в чем была допущена ошибка.

Для того чтобы понять, в чем ошибка, надо тщательно проанализировать процесс вывода формулы Харриса. Вернемся еще раз к выражению, описывающему полные затраты на заказывание и хранение.

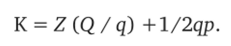
Мы видим, что во втором слагаемом норматив, характеризующий расходы, связанные с хранением товара умножаются на половину размера заказа. Напомним, это связано с тем, что при равномерном расходовании сырья его средний запас на складе равен половине его завоза на склад, а расходы на хранение, потери, проценты за кредит и т. п. считаются зависящими от средней величины запаса на складе.

Иное дело — арендная плата. После того как мы арендовали какую-то площадь под склад, мы вынуждены платить за всю площадь, независимо от того, что периодически склад бывает почти пуст. Площадь же мы должны арендовать в расчете не на средний, а на максимальный запас, т. е. на размер заказа.

Наша ошибка как раз и состояла в том, что мы не учли этот факт и в своих расчетах ставку арендной платы использовали точно так же, как и норматив потерь при хранении, хотя, еще раз отметим, первый из этих показателей зависит от максимальной величины заказа, на которую мы рассчитываем, а второй — от средней величины хранимого товара.

Из всего сказанного можно сделать вывод 2: при использовании формулы в неочевидных случаях расчеты по ней целесообразно дополнить проверкой методом «прямого счета», который, следуя логике вывода формулы, является в то же время более гибким и наглядным.

Можно предложить, по крайней мере, два метода исправления: один метод исправления расчета и один метод исправления формулы.

Исправить данный расчет можно корректировкой ставки арендной платы.

Легко видеть, что формула, приводя все расходы к средним за период, автоматически их «ополовинивает». Например, мы указываем проценты за кредит в расчете на месяц, а в формуле проценты берутся от стоимости заказа, но за полмесяца и т. д. Нам же нужно, чтобы арендная плата бралась за месяц. Для этого надо просто указать двойную ставку арендной платы.

Если мы теперь пересчитаем р, но ставку арендной платы возьмем двойной, то получим 280 руб. Подставляя 280 руб. в формулу, получаем: q = 12 677 тыс. руб., что ближе к 12 000 тыс., чем к 15 000 тыс. руб.

Но можно исправить и формулу. Для этого в выражение, описывающее суммарные затраты на заказывание и хранение, нужно включить третье слагаемое, которое будет учитывать затраты, зависящие от принятого решения относительно размера заказа, но не зависящие от фактической динамики материала на складе.

В данном случае это — арендная плата. Она зависит от нашего решения: завозить товар на склад столько-то раз и арендовать такую-то площадь, но не зависит от того, как будет использоваться склад. К таким же затратам могут относиться расходы на отопление, освещение, охлаждение, охрану склада и т. п., если они, с одной стороны, подконтрольны нам, т. е. зависят от нашего решения относительно размера заказа, а с другой — не регулируется в соответствии с наличием товара на складе.

Первое условие выполняется, если, например, как в данной задаче, мы можем выбрать под склад любую площадь и платить за аренду и обслуживание только этой площади.

Выполнение второго условия для охраны, например, очевидно, так как постоянно охраняется территория всего склада независимо от того, что часть хранилищ могут быть пустыми.

Упражнение 5.9.

Обозначим через, а ставку в расчете на 1 м² арендной платы и иных расходов, зависящих от размеров заказа, но не зависящих от динамики изменения запаса на складе.

Выведите формулу Харриса с учетом данных расходов.

Модификация формулы с целью приспособления ее для нужд конкретной задачи позволят сделать вывод 3: формулу Харриса можно совершенствовать.

Усложним задачу. Пусть в добавление к сформулированным ранее условиям требуется, чтобы на складе постоянно хранился запас товаров, достаточный для пяти дней работы магазина (магазин работает 30 дн. в месяц). Кроме того, указывается, что транспортные затраты (дополнительно к тому, что уже есть в условии) составляют 25 руб. на каждую 1000 руб.

Упражнение 5.10.

Решите задачу с этими дополнительными условиями, а потом сравните с решением, приведенным далее.

Прежде чем браться за решение новой задачи, надо проанализировать, что изменилось в ее условиях. И здесь уместно вспомнить, что все затраты, которые несет предприятие (в данном случае магазин), с рассматриваемой точки зрения можно разделить на три группы: затраты, в той или иной форме зависящие от числа заказов; затраты, в той или иной форме зависящие от размера заказа; затраты, не зависящие ни от числа заказов, ни от размера заказа.

Затраты первых двух групп нашли отражение в формуле Харриса. Затраты третьей группы, какими бы большими и важными для предприятия они ни были, в расчет при определении оптимальной складской политики не берутся и в формулу не включаются.

Если мы теперь под этим углом зрения посмотрим на новые данные, то увидим, что на процесс принятия решения в области складской политики они практически не влияют.

Транспортные затраты в задаче постоянны, так как зависят от объема закупаемого товара, который считается постоянным (60 000 тыс. руб.) и постоянного норматива транспортных затрат (25 руб. на 1000 руб. товаров), т. е. они равны 15 000 тыс. руб. независимо от того, сколько раз и какими партиями доставляется товар. Поэтому эти затраты в расчете можно вообще не учитывать. (Это не означает, что их нет. Это означает, что их величина не влияет на наше решение.).

Что касается страхового запаса, то это тоже постоянная величина, поэтому на наше решение об оптимальном числе заказов наличие стра;

хового запаса не влияет. Но на решение задачи влияет, так как помимо 48 м² склада для хранения рабочего запаса товара мы должны арендовать еще 40 м² под страховой запас (именно такую площадь занимает товар, обеспечивающий пять дней работы магазина), т. е. всего 88 м².

Не всякие данные, даже имеющие отношение к доставке и хранению товара, важны при принятии решения относительно оптимального размера заказа. Таков наш вывод 4.

Приблизим нашу задачу еще более к практике. Предположим, что при закупках большими партиями оптовые торговцы предоставляют скидки. Пусть при закупке на сумму 20 000 тыс. руб. и более предоставляется скидка 2%, на сумму 30 000 тыс. руб. и более — 5% и на сумму свыше 50 000 тыс. руб. — 8%. Пусть также каждый заказ и доставка товара на сумму меньшую 25 000 тыс. руб. стоят по-прежнему 375 тыс. руб., на сумму от 25 000 тыс. руб. до 49 000 тыс. руб. — 475 тыс. руб. (одного грузовика мало!), а от 50 000 тыс. руб. до 74 000 тыс. руб. — 575 тыс. руб. Как изменится решение задачи в этом случае?

Упражнение 5.11.

Ответьте на поставленный вопрос.

Как видим, теперь в задаче появилась скидка к цене закупки, хотя сама цена в формуле не фигурирует (там есть потребность, но она ведь может быть дана и в натуральных измерителях), а также изменяющиеся затраты на заказ и доставку товара.

Существуют приближенные алгоритмы решения подобных задач, основанные на формуле Харриса, однако в данном случае проще воспользоваться уже опробованным выше методом прямого счета, воспроизводящим логику вывода формулы. Решение приводится в табл. 5.2.

В строке 1 представлен размер заказа с учетом указанных скидок.

Арендуемые площади остаются теми же самыми, т. е. считается (это вполне разумно), что скидка не влияет на норматив.

Поскольку изменилась среднемесячная стоимость хранимого товара, то, естественно, изменилась стоимость потерь и процент за кредит.

В табл. 5.2 соответствующим образом изменены и затраты на хранение, хотя это, вообще говоря, спорно: возможно, их, как и арендную плату, надо считать от стоимости заказа без скидки. Как правильно — зависит от конкретной ситуации, но в целом ошибка будет не очень большой.

Таблица 5.2

Затраты предприятия при разном количестве заказов в месяц.

В строке 8 приведена скидка, полученная за все заказы. Например, для двух заказов получаем: (30 000 — 28 500) • 2 = 3000 тыс. руб. Далее эта скидка рассматривается как частичная компенсация затрат на хранение и заказывание, поэтому строка 10 представляет собой сумму строк 3, 5, 6, 7, 9 за вычетом строки 8.

Как видно из последней итоговой строки, при заданных условиях ориентация хозяйственной практики на два заказа в месяц позволяет существенно снизить суммарные затраты.

Приведенный выше расчет позволяет сделать вывод 5: метод прямого счета должен рассматриваться не только как способ проверки полученных результатов, но и как высокоэффективный метод оптимизации размера заказа, позволяющий учесть в расчетах ряд дополнительных параметров, существенно актуализирующих решение.

Наконец, общий вывод таков: формула Харриса — своего рода программа действий, легко приспосабливаемая к конкретным условиям