Методы кластеризации. 
Программная инженерия и технологии программирования сложных систем

Стоит также упомянуть о методе кластеризации. Данный метод можно исследовать с применением метода^{-ближайших} соседей (что является основой алгоритма Microsoft Clustering). Суть его в следующем. Предположим, что нам необходимо классифицировать объект 5, признаковое описание которого представлено вектором x (S). Для каждого из классов К_ь …, вычисляется условная вероятность принадлежности Р (К_{х). Объект S относится к тому классу, для которого условная вероятность принадлежности максимальна. Данное решающее правило минимизирует вероятность ошибочной классификации. Его обычно называют байесовским решающим правилом или оптимальным байесовским классификатором. К сожалению, байесовское решающее правило не может быть реализовано в подавляющем большинстве практических задач из-за того, что вероятностное распределение неизвестно.

Однако мы можем попытаться оценить условные вероятности принадлежности P (Kjx), используя информацию, содержащуюся в обучающей выборке.

Метод^{-ближайших} соседей Оценка условной вероятности P (Kjx) в методе^{-ближайших} соседей ведется по ближайшей окрестности V_k точки x (S) в признаковом пространстве, содержащей, но крайней мере k признаковых описаний объектов обу;

k

чающей выборки. В качестве оценки Р (К.х) выступает отношениеS где.

k

k_i — число объектов из класса Kj в окрестности V_k. Естественно, что поиск ближайшей окрестности должен основываться на использовании некоторой функции расстояний, заданной на множестве пар точек признакового пространства. В качестве такой функции расстояний, в частности, может выступать евклидова метрика. Точность распознавания методом^{-ближайших} соседей существенно зависит от числа k, оптимизация которого может производиться по обучающей выборке. При этом в качестве оптимального берется то число ближайших соседей, при котором оценка точности распознавания с использованием режима скользящего контроля максимальна. Основным недостатком метода^{-ближайших} соседей является снижение его эффективности при малых объемах выборки и высокой размерности признакового пространства.

Данный алгоритм можно разбить на следующие шаги.

Шаг 1. Выбираются k исходных центров кластеров z/j (/), z/₂(/), …, yfij) zfil), z₂(/),…, z_k(l). Этот выбор производится произвольно, например первые k результатов выборки из заданного множества объектов.

Шаг /. На /-м шаге итерации заданное множество объектов {х} распределяется по k группировкам, но следующему правилу:

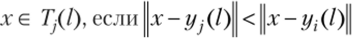
для всех i = 1,2,…, k, i Ф j, где Tfil) — множество образов, входящих в кластер с центром у fit). В случае равенства решение принимается произвольным образом.

Шаг /+ 1. На основе результатов шага / определяются новые центры группировок yfil + 1), у = 1,2, …, k, исходя из условия, что сумма квадратов расстояний между всеми объектами, принадлежащими множеству Tfil)_f и новым центром данной группировки должна быть минимальной.

Центр yfil +1), обеспечивающий минимизацию ,.

7=1,2, …, /г, является выборочным средним, определенным по множеству Tfil). Следовательно, новые центры кластеров определяются как.

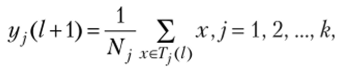
где Nj — число выборочных объектов, входящих в множество Tfil). Очевидно, что название алгоритма «k внутригрупповых средних» определяется способом, принятым для последовательной коррекции назначения центров кластеров.

Равенство у0 + 1) = zfil) при 7=1,2, …, k является условием сходимости алгоритма, и при его достижении выполнение алгоритма заканчивается. Полученные множества T:(l)>j= 1, 2,/е, образуют искомые кластеры. В противном случае последний шаг повторяется.

В противовес данному алгоритму можно поставить алгоритм локализации аномалий с применением метода кластеризации.