Методы математических доказательств

Понятие доказательства. Правила вывода

Доказать предложение означает установить его истинность.

Процесс доказательства осуществляется по следующей схеме: строят последовательность предложений А, A_h А₂, А_п, В, при этом для каждого предложения, начиная со второго, либо обосновывается его истинность, либо говорится о том, что оно следует из предыдущих предложений. Приведенная цепочка утверждений позволяет заключить, что из А следует В. Напомним, что предложение Q называется следствием предложения Р, если всегда, когда верно Р, верно и Q.

Доказательство, в общем случае, носит условный характер. Изначально выбирается некоторое предположение А (например, условие теоремы), и исходя из истинности этого предложения обосновывается истинность предложения В. Если же известно, что А является истинным высказыванием (например, А — это ранее доказанная теорема или аксиома), то данная цепочка предложений доказывает, что и предложение В является истинным высказыванием.

Пример 5.1.1. Проведем доказательство предложения «Сумма квадратов двух четных чисел делится на 4».

Введем обозначения.

А = «Числа х и у четные»,.

А = «л: и у имеют вид х=2п, у=2к, где п, к — целые числа»,.

А₂ = «х² +у²=4т, где т — целое число»,.

В = «Сумма х²+у² делится на 4».

Запишем процесс доказательства: «По определению четного числа из А следует А,. По законам операций сложения и умножения из А| следует А₂. Действительно, пусть х и у имеют вид х=2/?, у=2к, где п, к — целые числа. Тогда сумма их квадратов равна х²+у² = (2п)²+(2к)² = 4/Г+4Л^ = 4(л²+&²) = 4 т, где т=п²+!?- целое число. По определению делимости целых чисел из Л₂ следует В».

Схематично процесс доказательства можно записать в виде:

На основании приведенных рассуждений можно утверждать, что из А следует В, то есть для любых четных чисел х и у сумма их квадратов делится на 4. Исходное предложение доказано. •.

В рассмотренном примере для обоснования того, что из А следует Л₂, мы воспользовались общими свойствами операций: (ab)² = а²Ь², 4я+4/> = 4(я+6), при этом совершенно неважно, какие числовые значения принимают буквы а и Ь.

Аналогичным образом можно выделить общие свойства на множестве формул логики, которые позволяют при любых исходных предложениях получать определенные следствия. Например, для любого предиката А (х)> где х обозначает произвольное действительное число, из любого предложения вида Vx/4(jc) следует предложение 3хА (х). Действительно, если предложение истинно для каждого числа л;, то, взяв вместо х, например, число 1, истинным будет предложение А ( 1). Поэтому наверняка существует число, удовлетворяющее свойству А. При этом совсем неважно, какой именно предикат обозначает буква А.

Правила, позволяющие получать следствия независимо от содержания предложений, называют правшами вывода. Отметим, что правила вывода — наряду с тавтологиями и равносильностями — можно отнести к законам логики.

Каждое правило вывода представляет собой последовательность формул (F_h F₂, F", Р), где формулы F, называются посылками (или гипотезами), а формула Р называется

заключение

м (или следствием).

Указанное правило кратко обозначают следующим образом: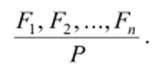

С логической точки зрения каждое такое правило вывода означает, что всегда, когда каждая из формул F, F₂, …" F" обозначает истинное высказывание, формула Р также будет истинным высказыванием. Другими словами, формула (FaF₂a…aF") —> Р является истинной при всех значениях переменных, от которых она зависит. Напомним, что такие формулы в логике называются тавтологиями (используются и другие термины: «общезначимая формула», «логический закон»). Каждое правило вывода можно записать, используя знак отношения следования: (F]aF₂a…aF") => Р.

Рассмотрим правило отделения (modus ponens) ^^ ^ (1).

Здесь А и В могут обозначать произвольные предложения, возможно, зависящие от предметных переменных. Болес того, под А и В можно понимать произвольные формулы.

Правило (1) является одним из основных правил, применяемых в доказательствах. Обычно это делается неосознанно или по умолчанию. Опишем суть этого правила. Предположим, что в процессе доказательства выведено предложение А и обосновано, что из А следует В, то сеть доказана импликация Тогда можно сделать вывод о том, что отсюда следует предложение В.

Пример 5.1.2. Пусть в процессе доказательства получено, что целое число х делится на 4 (заметим, что здесь нет квангорного слова и мы имеем предикат, который является следствием каких-то предложений, например следствием условий теоремы).

Обозначим: А = «х делится на 4», В = «х — четное».

Так как любое число, делящееся на 4, является четным, то истинна импликация А —" В. На основании правила (1) можно сделать вывод: число х четное. •.

Последовательность предложений, построенных по правилу вывода, называется правильным рассуждением.

По данным примера 5.1.2 построим правильное рассуждение: «Пусть число делится на 4. Если число делится на 4, то оно является четным. Следовательно, данное число является четным».

Остановимся на случае, когда предложения зависят от переменной л: (как в предыдущем примере). Предположим, что предложение А является истинным при всех допустимых значениях х (такое предложение называется тождественно истинным) и из предложения А следует В, то есть формула А—>В тождественно истинна. Тогда можно сделать вывод о том, что и предложение В является тождественно истинным.

Имеем правило:

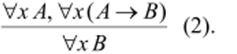
Пример 5.1.3. Пусть известно (ранее доказано), что квадрат любого действительного числа неотрицателен и любое число, противоположное неотрицательному числу, является неположительным.

Рассмотрим два предиката: А = (х²>0), В = (-х²<0).

Используя указанные факты, имеем: А — тождественно истинный предикат, и из А следует В. Значит, по правилу (2) предикат В является тождественно истинным. Итак, доказано, что неравенствох <�Ю верно при всех действительных значениях х. •

С помощью таблицы истинности нетрудно доказать, что формула [(А^>В)л (В—«С)]—"(Л—>С) является тавтологией. Отсюда можно получить следующее правило:

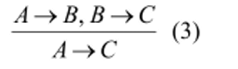
В логике схему (3) называют правилом силлогизма (цепного вывода).

Подчеркнем, что правила вывода нужно применять следующим образом. Пусть в процессе доказательства получены предложения, расположенные над чертой. Тогда можно вывести предложение, записанное под чертой.

Пример 5.1.4. Обозначим А = «х — целое число», В = <<�х — натуральное число", С = «2х — натуральное число».

Если в доказательстве буква х обозначает произвольное число, то посылка А—>В при некоторых х является ложным высказыванием (например, при х= -2). Поэтому импликация А—>С нс обязана быть истинным высказыванием дня произвольного числа дг. В этом случае применять правило (3) нельзя. Тем не менее если мы возьмем такое число, при котором обе посылки верны, то заключение для этого же числа будет истинным высказыванием.

Предположим, что исходя из условий теоремы доказано: х есть положительное число. Тогда импликация А^>В принимает истинное значение для такого значения * (так как любое положительное целое число является натуральным). Заметим, что импликация Я-«С всегда истинна. Поэтому теперь можно воспользоваться правилом (3). •.

Рассмотрим другой пример.

Пример 5.1.5. Обозначим А = «х — натуральное число», В = «х — целое число», С = «х- рациональное число».

Так как любое натуральное число является целым, а любое целое является рациональным (целое число а можно представить в виде дроби с числителем а и знаменателем 1), то обе импликации А->В и В->С — это истинные высказывания при всех х. Отсюда можно заключить, что импликация А—>С всегда принимает истинное значение. •.

Итак, если предикаты А> В и С зависят от переменной .v, то имеет место следующее правило:

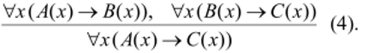
Пример 5.1.6. На основе правила (4) построим рассуждение: «Все квадраты являются ромбами. В любом ромбе диагонали перпендикулярны. Следовательно, в каждом квадрате диагонали перпендикулярны».

Если уже доказана истинность двух исходных предложений, то приведенное рассуждение доказывает истинность заключения. •.

Рассмотрим еще одно правило вывода. Для этого выведем следствие из предложений V* (/!(*)->#(*)) и Т#(у), где Ли В — это произвольные предикаты, зависящие от одной переменной.

Пусть предложения Vx (А (х)->В (х)) и 1В (у) одновременно истинны. Тогда импликация А (х) —>В (х) истинна при всех х, а В (у) — ложно. Подставим вместо переменной х значение _у, тогда А{у)^>В (у) будет истинным высказыванием. По определению импликации, так как она принимает истинное значение, а предложение В (у) ложно, то предложение А (у) является ложным. Поэтому 1А (у) истинно. Итак, имеем правило:

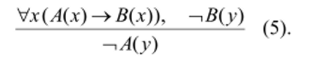
Здесь буквы А и В обозначают произвольные предложения, а буква у — произвольное значение, допустимое для предложений А и В.

Пример 5.1.7. Предположим, что нам известны два факта: любое натуральное число является целым, а число л («пи») не является целым. Докажем, не используя больше никаких математических знаний из школьного курса (опираясь только на логику), следующую теорему: «Число л не является натуральным».

Введем обозначения: А (х) = «Число, т натуральное», В{х) = «Число, т целое». Переменная х обозначает число.

Тогда формула 1#(л) обозначает предложение «Число л не целое», формула /х (Л (л) —>В (х)) — предложение «Любое натуральное число является целым», а формула ~А (п) — предложение «Число л не натуральное».

Известные нам факты — это посылки правила (5). Применяя это правило, делаем заключение: «Число л не является натуральным». Теорема доказана. •.

Замечание. Рассмотренные выше правила вывода можно сформулировать на языке отношения следования:

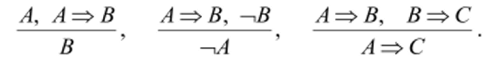
Например, последнее правило интерпретируется следующим образом: если доказано, что из предложения А следует предложение /?, а из В следует С, то можно заключить, что из А следует С. Это правило дает возможность доказывать теоремы методом последовательного выведения следствий: А] => А₂ =>…=> А_п.

Рассмотрим доказательство одного утверждения и попытаемся выделить используемые правила вывода.

Пример 5.1.8. Докажем предложение «Квадрат ненулевого действительного числа положителен».

Доказательство. Пусть х — действительное число. Покажем, что если х не равно 0, то .г больше 0.

Известно, что любое действительное число является либо положительным, либо отрицательным, либо равно 0. Поэтому если х не равно 0, то оно положительное или отрицательное.

Если .V положительное, то его квадрат положителен (по правилу умножения чисел). Если д; отрицательное, то его квадрат также положителен (снова по правилу умножения чисел).

Следовательно, если * не равно 0, квадрат х положителен. Утверждение доказано.

Проведем анализ такого доказательства. Введем обозначения.

А = (л*0), В = (лг>0), С = (л<0), D = (х² >0).

Запишем цепочку предложений, составляющих доказательство, указывая в скобках соответствующую формулу.

• 1. Известно, что число х либо равно 0, либо является положительным, либо отрицательным (!/!(*)vZ?(.v)vC (.x) или, сокращенно, ~Uv/?vC).
• 2. Поэтому если дне равно 0, то оно положительное или отрицательное (A->(BvQ).
• 3. Если х положительное, то его квадрат положителен (?—"D).
• 4. Если х отрицательное, то его квадрат также положителен (C->D).
• 5. Следовательно, если х не равно 0, квадрат * положителен (A—>D).

Первое предложение верно для любого числа х. Однако в дальнейших рассуждениях кванторные слова не используются. Здесь работает так называемое правило удаления квантора общности', так как предложение верно для всех объектов, то этот объект можно обозначить какой-то буквой и вести дальнейшие рассуждения об этом объекте, используя взятую букву. Строго говоря, вначале мы имеем формулу V. t [" U (.t)v/?(a*)vC (jc)], из которой удаляем квантор общности.

А v В v С

Второе предложение получено по такому правилу: -. Это Л—>(#vC).

правило не зависит от конкретного содержания предложений А, В и С. Для его логического обоснования можно построить таблицу истинности.

Третья и четвертая импликации верны для всех объектов дг. Удаляя квантор общности, получаем указанные предложения.

На каком основании получено пятое предложение? При получении этого предложения были одновременно применены два правила. Выделим их.

Из третьего и четвертого предложений следует такое: «Если число х положительное или отрицательное, то х положительное число».

₀ В —> А С —> D

Вывод получен на основании правила ————-, которое опять же можно применять независимо от содержания предложений В, С и D. Проверьте справедливость этого правила с помощью таблицы истинности.

Теперь мы имеем предложение вида (BvC)—>D. Учитывая второе предложение и применяя правило цепного вывода (3), получаем пятое предложение. Действительно, из формул A—>(BvC) и (BvC)->D следует формула A—>D.

Так как все рассуждения были проведены дзя произвольно взятого числа х, то импликация Л->?> верна для всех х. Здесь мы вернули квантор общности, удаленный в процессе доказательства. В этом случае говорят, что применили правило обобщения (или правило введения квантора общности).

Итак, доказано, что квадрат любого ненулевого действительного числа положителен. •.

Отметим, что возможность формулировать теорему, удаляя (или восстанавливая) внешний квантор общности, о чем шла речь в пункте 4.1, согласуется с правилом удаления квантора общности и правилом обобщения.

Остановимся на какое-то время на правиле обобщения. Несмотря на простоту этого принципа, он имеет большое значение, так как даст возможность проводить рассуждения, оперируя с фиксированной буквой.

(которая обозначает произвольное значение), а затем делать вывод о том, что полученное предложение верно при всех значениях, которые обозначает выбранная буква. С другой стороны, применять правило обобщения нужно аккуратно. Например, если в процессе доказательства буква обозначает какой-то конкретный объект, то применять правило обобщения по этой букве нельзя.

Пусть требуется доказать утверждение VxP (x) = «Для всех дг верно Р (х)». Для этого выбирают произвольную букву а и доказывают, что Р (а) истинно. В этом случае доказательство обычно начинают словами: «Возьмем (рассмотрим, зафиксируем) произвольный элемент а». Также говорят: «Пусть а — произвольный элемент». В зависимости от контекста на выбранный произвольно элемент а, конечно, накладываются определенные ограничения; например, а может обозначать произвольное целое число. Вместо буквы а можно взять другую букву. Часто оставляют букву х. Однако в дальнейших рассуждениях буква .г фигурирует уже как конкретный объект (он выбран произвольно и после этого зафиксирован).

После того как обоснована истинность Р (а), делают вывод, что доказано исходное предложение /хР (х).

Если предложение Р (х) имеет вид импликации А (х)—>В (х)_у то доказательство начинают фразой: «Пусть, v — произвольный элемент, такой, что Л (х)». Далее из А (х) выводят следствия и получают В (х). После этого по правилу обобщения заключают, что импликация А (х)->В (х) истинна при всех допустимых значениях х.

Пример 5.1.9. Докажем, что любое целое число, делящееся на 4, является четным. Истинностью этого утверждения мы пользовались в примере 5.1.2.

Доказательство. Пусть целое число дг делится на 4. Тогда д имеет вид дс=4я, где п — целое число (заметим, что здесь п обозначает не любое целое число, а вполне конкретное число, зависящее от значения х). Значит, х имеет вид х = 2(2п) = 2т, т — целое. Поэтому д; - четное число.

Итак, при любом значении jc, если х делится на 4, то д: есть четное число.•.

Приведем пример схемы, с помощью которой из истинных предложений можно получить ложное высказывание. Естественно, такую схему нельзя использовать при доказательстве.

Исходные высказывания: F = Зх (А (х)лВ (х)), F₂ = Зх (В (х)лС (х)).

Получаемая формула: Р = Зд- (Л (лг)лС (л)).

Нс всегда, когда истинны предложения F и F₂, обязано быть истинным предложение Р.

Пример 5.1.10. F = «Существует положительное число, являющееся целым».

F₂ = «Существует целое число, являющееся отрицательным».

Р = «Существует число, являющееся положительным и огри цател ьным».

Высказывания F и F₂ истинны, а высказывание Р ложно. •.

Замечание. Современная математическая логика позволяет получать правила вывода формально-аксиоматическим путем, то есть без использования содержательных рассуждений и опоры на истину и ложь, что позволяет дать понятию доказательства строгое определение. В нашем изложении материала правила вывода нельзя считать фундаментом понятия доказательства: так, для того чтобы получить даже самые простые правила, нам приходится их доказывать, что напоминает порочный круг.

В контексте данного пособия правило обобщения, например, воспринимается как понятный факт. Раз обосновано, что верно Р (а), где а обозначает произвольный, пусть и фиксированный объект, то обосновано утверждение /хР (х). При формальном подходе это правило может быть просто взято за основу без каких-либо комментариев и доказательств.