Исследование фазового и химического равновесия

Описание фазового равновесия является одной из важнейших задач при расчете процессов разделения. Знание условий равновесия позволяет не только принципиально решить вопрос о возможности разделения многокомпонентной смеси методами ректификации, абсорбции, экстракции, но и выбрать схему разделения. Наиболее общий метод расчета равновесия основан на применении некоторого уравнения (уравнения состояния) ко всем фазам системы пар — жидкость. Однако использование уравнений состояния возможно лишь в случае простых систем, которые образованы веществами с аналогичными свойствами, например неполярными веществами, составляющими природный газ.

При наличии полярных молекул эти уравнения непригодны. Для таких систем, составляющих в большинстве своем процессы основной химии, уравнения состояния применяют только для паровой фазы, а жидкая фаза рассматривается с учетом отклонений от идеального поведения для реальных условий смешения и в соответствии с теорией растворов.

При рассмотрении многофазных систем достижение фазового равновесия интерпретируется как состояние, при котором скорости взаимного перехода молекул компонента из одной фазы в другую равны между собой. Термодинамически это условие выражается как равенство химических потенциалов фаз по каждому компоненту, т. е.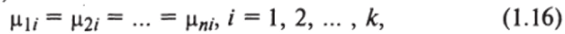

где ц/ - химический потенциал, равный частной производной от изобарноизотермического потенциала (свободной энергии Гиббса) по составу при постоянных давлении и температуре системы.

Для химической реакции, протекающей в идеальной газовой фазе, имеем.

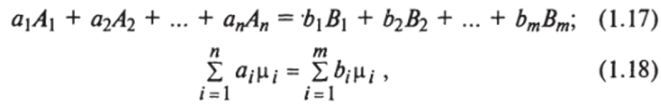
где д" bj — стехиометрические коэффициенты исходных веществ и конечных продуктов реакции; A_it Bj — наименование исходных компонентов и продуктов реакции.

Если в (1.18) подставить выражение для химического потенциала Ц/ = ро + Я Tin/>, то после соответствующих преобразований для константы химического равновесия можно записать.

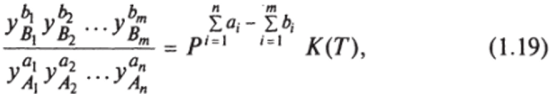
где У^.₉УВ{ ~ концентрации исходных компонентов газовой смеси и продуктов реакции соответственно; Р — давление системы; К — константа равновесия химической реакции.

Из (1.19) следует, что при изменении давления равновесный состав будет меняться в зависимости от соотношения стехиометрических коэффициентов а, и Ь,. Если реакция идет без из;

п m

менения общего числа молей в системе (т. е.? я/ = Z b_t), то.

/=1 /=1.

давление не влияет на равновесный состав. Температурная зависимость равновесного состава определяется характером температурной зависимости константы равновесия (возрастающей или убывающей функцией температуры). Заметим, что уравнение (1.19) носит название «закона действующих масс».

Если некоторые из компонентов реакции (1.17) находятся в конденсированном состоянии, то при незначительных изменениях внешнего давления концентрации их не указываются в левой части уравнения (1.19), однако при вычислении константы равновесия через свободную энергию Гиббса конденсированное состояние этих компонентов учитывается.

Поскольку фазовое равновесие в замкнутых системах достигается при наличии в системе химического равновесия, очевидно, что расчет равновесия в системах, в которых происходит несколько одновременно протекающих реакций, представляет определенные трудности.

Недостатком описания условий фазового равновесия через химические потенциалы является то, что эти величины измерить непосредственно невозможно. Поэтому для получения расчетных соотношений необходимо выразить их через параметры состояния системы. Такой подход термодинамически обоснован при рассмотрении идеальных систем, когда имеется уравнение состояния. Однако для реальных систем до настоящего времени отсутствует общепринятое уравнение состояния реального газа, в связи с чем вывод соотношений для термодинамических функций и описание условий фазового равновесия крайне затруднено. С использованием функции фугитивности условие равновесия реальных систем выражается как.

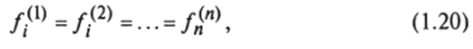
где — фугитивность, определяемая тем, что, во-первых, термодинамические соотношения справедливы для идеальных и реальных систем; во-вторых, совпадает с давлением, если последнее настолько мало, что газ становится идеальным.

Если рассматривать идеальный раствор как смесь компонентов, молекулы которой ведут себя так же, как и в чистой жидкости, а неидеальность поведения отразить введением меры неидеальности в виде коэффициентов, то фугитивности отдельных компонентов должны быть пропорциональны их концентрациям, т. е. для двухфазной системы имеем:

где у;, ф, — коэффициенты, характеризующие неидеальность жидкой и паровой фаз, т. с. коэффициенты активности и летучести соответственно: /,° ,//^ - фугитивности компонентов в стандартных условиях (L — жидкость; V — пар); х,-, уj — мольные концентрации жидкой и паровой фаз соответственно.

Если паровая фаза подчиняется законам идеальных газов, то вместо можно использовать Р (давление системы). Аналогично при умеренных давлениях вместо f^^L можно использовать Рj° (давление пара чистого компонента). Таким образом, условие равновесия для любого компонента трехфазной многокомпонентной смеси запишется как.

Это уравнение является основным при расчете фазового равновесия многокомпонентных трехфазных систем. Коэффициенты активности и летучести, как мера отклонения фаз от идеальности, для идеальной смеси равны единице.

Как следует из уравнения (1.21), параметры, характеризующие условия равновесия (состав, температура, давление), могут быть рассчитаны лишь при наличии значений фугитивности в стандартном состоянии. В принципе выбор стандартного состояния произволен и диктуется лишь удобствами расчета. Необходимо только, чтобы стандартные фугитивности вычислялись при той же температуре, что и температура смеси. Давление и состав могут выбираться произвольно.

Изменение потенциала при смешении двух растворов в изобарно-изотермических условиях составляет.

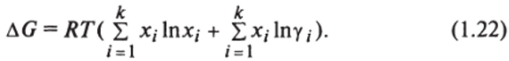
Первый член этого выражения соответствует изменению потенциала при смешении идеальных компонентов, а второй — изменению потенциала за счет неидеальности смеси. Таким образом, избыточная свободная энергия смешения Гиббса равна:

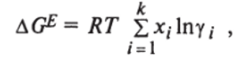
где хi — средняя мольная доля i-го компонента,.

ИЛИ

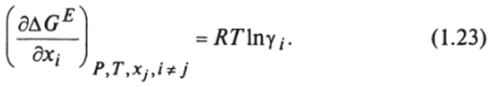
Поскольку избыточная энергия является мерой неидеальности смеси, выражение (1.23) широко используется для оценки степени этой неидеальности.

В соответствии с моделью Вильсона, в которой он ввел понятие «локальные» объемные доли компонентов, уравнение (1.23) приобретает вид для свободной энергии смешения:

где — локальная объемная доля /-го компонента относительно центральной молекулы того же типа; G^E — свободная энергия смешения Гиббса.

Основная идея этой концепции заключается в том, что при микроскопическом рассмотрении жидкая смесь не является однородной. Состав в одной точке смеси может отличаться от состава в другой. Хотя в инженерных приложениях и используется только средняя концентрация компонентов в смесях, для построения адекватной модели жидкой смеси необходимо оперировать локальными составами. Согласно концепции локальных составов, введенной Вильсоном, распределение молекул относительно центральной молекулы имеет вид:

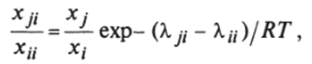
где Xji — локальный состав, определенный как число молекул типа ] - / в окрестности центральной молекулы, деленное на общее число молекул; (Хд — Хд) — параметр, характеризующий энергию взаимодействия между парами i — / и С учетом введенных локальных концентраций локальные объемные доли /-го компонента в уравнении (1.24) могут быть определены как.

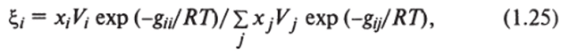
где V" Vj — мольные объемы чистых / и j компонентов; gy = Ху - X#; gji ⁼ — Хд.

Подстановкой уравнения (1.25) в (1.24) получаем зависимость избыточной энергии смешения Гиббса от состава и температуры смеси. Дифференцирование полученного выражения по составу смеси дает широкоизвестное уравнение Вильсона, связывающее коэффициент активности компонента в смеси у, с составом и температурой смеси:

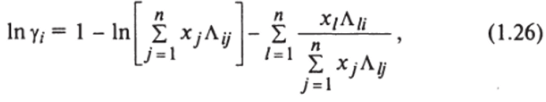
где.

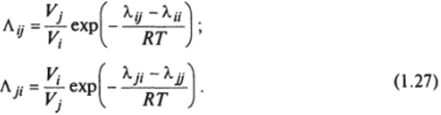
Модель Вильсона требует для описания состояния равновесия многокомпонентных смесей (МКС) только задания экспериментальных данных по бинарным парам, входящим в данную МКС, и физико-химических свойств чистых компонентов.

Равновесная концентрация /-го компонента в л-компонентной смеси выражается как:

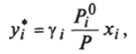
где Р® — упругость паров чистого компонента; Р — давление в системе, МПа.

Коэффициент активности любого компонента у/ можно определить из уравнения (1.26), а коэффициент активности в бинарной паре — рассчитать по следующим уравнениям:

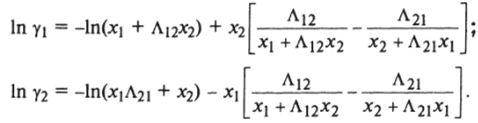
Упругость паров /-го компонента Я,⁰ рассчитывается по уравнению Антуана:

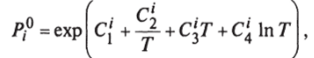
где Cj ,., Cj — эмпирические константы, определяемые по методу наименьших квадратов.

Алгоритм определения равновесной концентрации у* = / (х,) следующий: определяются параметры k/j — ц и — kjj из уравнений (1.27) для всех пар компонентов, составляющих МКС, по экспериментальным данным бинарного равновесия. Решение проводится методом последовательных приближений, причем степень приближения контролируют по суммам квадратов отклонений равновесных составов паровой фазы в контрольных точках, рассчитанных и снятых экспериментально. Направление поиска неизвестных параметров указывает минимизируемая функция R:

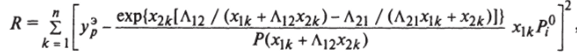
где к = 1, 2, …, m — число контрольных точек; усостав паровой фазы в контрольной точке.

Алгоритм поиска должен быть составлен таким образом, чтобы можно было определить значения неизвестных параметров Х[2 — А. ц и Х21 — Х22, которые удовлетворяли бы условию минимизации R = R_mm с заданной точностью.

На первом этапе расчета определяют оптимальные значения X. J2 — Хц и Л-21 — А.22, функцию R в оптимальной точке, коэффициенты активности у* бинарных систем в контрольных точках, состав паровой фазы у* для бинарных пар и относительную погрешность расчета состава паровой фазы.

На втором этапе при температуре смеси t = г_нач рассчитывают коэффициенты активности у, МКС по уравнению (1.26), а затем состав ее паровой фазы. Далее определяют температуру МКС, я •.

при которой удовлетворяется соотношение X У/ - 1 ^ е, что.

/=1.

соответствует условию термодинамического равновесия.

Эта методика расчета равновесия дает хорошие результаты как для бинарных, так и многокомпонентных систем. Однако уравнение Вильсона (1.26) применимо только для гомогенных жидких систем. Рядом исследователей выполнено его распространение на частично расслаивающиеся смеси.

Многочисленные исследования показали, что из всех уравнений, основанных на использовании данных по равновесию бинарных пар — Маргулеса, Редлиха-Кистера, Ван Лаара и т. д. — лишь уравнение Вильсона для гомогенных систем обеспечивает точность, сравнимую с точностью эксперимента.

Концепция локального состава используется также при выводе другого уравнения для описания фазового равновесия частично смешивающихся систем — уравнения NRTL. Предполагается, что раствор состоит из ячеек двух сортов с молекулами первого и второго типов в центре. Избыточная свободная энергия такого двухжидкостного раствора выражается через мольно-взвешенную энергию гипотетических жидкостей, включающих ячейки первого и второго типа. Используя двухжидкостную модель раствора и вводя концепцию локальных составов с модификацией исходного соотношения, применяя дополнительный параметр сцг, характеризующий неоднородность смешения, Праузниц и Ренон предложили для расчета коэффициентов активности следующее выражение.

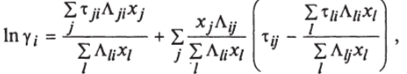
где.

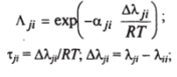
Xj" ^ti — экспериментально определяемые параметры.

Концепция локального состава легко сочетается с идеей функциональных групп, которая заключается в том, что термодинамические свойства жидкостей, содержащих полиатомные молекулы, могут быть рассчитаны по взаимодействию групп, из которых состоят молекулы. Так, молекула ацетона содержит две функциональные группы: СН3- и СН3СО-, а толуола — шесть групп: пять СН-групп и одну ССН3-.

Метод функциональных групп для расчета коэффициентов активности основан на следующих допущениях:

1) жидкий раствор можно рассматривать как раствор, состоящий из групп (которые выбираются как удобные структурные блоки) типа СН₃-, СН2О-, CH2NO2- и т. д.;

2) избыточная свободная энергия раствора предполагается равной сумме двух составляющих: одна связана с разностью размера молекул и формы, а другая — с энергетическим взаимодействием между группами

С R

где у; - комбинаторная (энтропийная) составляющая; у, — резидентная.

• (энтальпийная) составляющая;
• 3) вклад взаимодействия групп, т. е. разностная часть, предполагается равным сумме индивидуальных вкладов каждой группы в растворе минус сумма вкладов чистых компонентов, т. е.

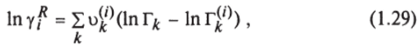
где к = 1,2… N, N — число различных групп в смеси; Г* - разностный коэффициент активности группы к в смеси; Г*'* - остаточный коэффициент активности группы к в стандартном растворе, содержащем только молекулы типа /; - число групп типа к в молекуле /;

4) индивидуальные вклады групп в некотором растворе, содержащем группы вида , 2,…, N, полагаются только функциями концентрации групп и температуры.

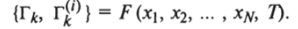
Для Г*, г}™ используются одинаковые функциональные зависимости. Концентрация х_к групп определяется как.

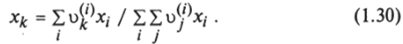
Различие между моделями функциональных групп обусловлено различием в определении групп и составляющих избыточной свободной энергии.

Наибольшее распространение получил метод UNIFAC, в котором составляющие коэффициента активности — комбинатор;

С R

ная у/ и резидентная у, — - рассчитываются следующим образом.

1. Комбинаторная составляющая коэффициента активности имеет вид:

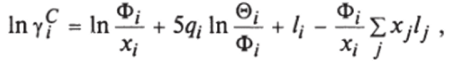
где .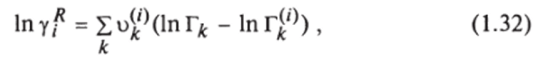

Ф/ - объемная доля /-го компонента; ©, — доля поверхности молекулы /-го компонента; г, — относительный ван-дер-ваальсовский объем /-го компонента; - относительная молекулярная поверхность /-го компонента; г, — рассчиты

ваются как суммы групповых параметров R* и 0*; У_ык — ван-дер-ваальсовский групповой объем; А^_к — площадь поверхности к-й группы.

2. Для резидентной составляющей коэффициента активности имеется выражение.

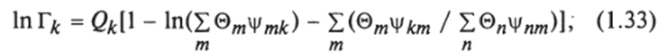
где и** - число групп типа к в /-Й молекуле; Г* - резидентный коэффициент.

активности группы к в смеси; - резидентный коэффициент активности группы к в чистом /-м компоненте.

Коэффициенты активности Г* и Г* рассчитываются из следующих выражений:

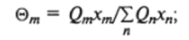
где Q_k - поверхность группы к.

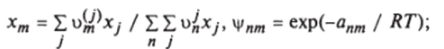
Э_т — поверхностная доля группы т, х_т — мольная доля группы т в смеси:

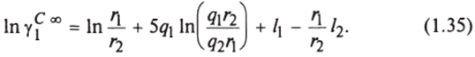
Ум — параметр модели UNIFAC; R - универсальная газовая постоянная; Т - температура; а^ - параметр группового взаимодействия, является мерой энергии взаимодействия между группами лит.

При бесконечном растворении компонента 1 компонентом 2 (см. разд. 1.1.5.1) (xi -> О, Х2 -> 1) получим следующее уравнение:

Комбинаторная часть рассчитывается по уравнению.

Для резидентной части UNIFAC соответственно получим:

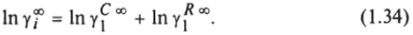
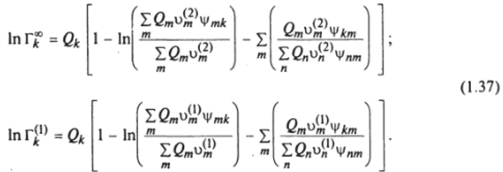
где.

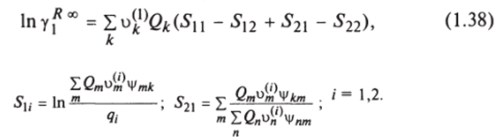
Подставляя (1.37) в (1.36), получим:

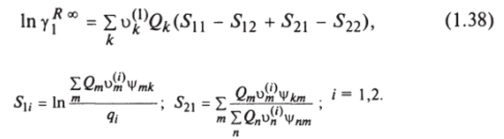
где Для того чтобы воспользоваться предложенным методом расчета коэффициентов активности, необходимо знать:

• 1) число функциональных групп и соответственно их объемы и площади;
• 2) значения параметров взаимодействия групп, которые рассчитываются на основании данных по фазовому равновесию (в настоящее время для основных групп эти параметры известны, что позволяет рассчитывать равновесие почти 70% всех опубликованных данных).

Главное достоинство этого метода состоит в его применимости к расчету систем, для которых отсутствуют экспериментальные равновесные данные, однако по сравнению с методами Вильсона и NRTL он обладает меньшей точностью.