Оценка проектов с неравными сроками действия

В реальной жизни вполне вероятна ситуация, когда необходимо сравнивать проекты разной продолжительности. Речь может идти как о независимых, так и об альтернативных проектах. В частности, сравнение независимых проектов может иметь место, когда заранее не известен объем доступных источников финансирования. В этом случае проводится ранжирование проектов по степени их приоритетности, т. е. они словно выстраиваются в очередь, и по мере появления финансовых возможностей проекты последовательно принимаются к внедрению.

Рассмотрим следующую ситуацию. Имеется два независимых проекта со следующими характеристиками (млн руб.):

А: -100, 120;

В: -50,30,40,15.

Требуется ранжировать их по степени приоритетности, если цена капитала 10%.

Значения NPV при СС = 10% и IRR для этих проектов соответственно равны:

На первый взгляд, можно сделать вывод, что по всем параметрам проект В более предпочтителен. Однако насколько правомочен такой вывод?

Сразу же бросается в глаза временная несопоставимость проектов: первый рассчитан на один год, второй — на три. Сравнивая проекты по критерию NPV, мы как бы автоматически выравниваем их по продолжительности, неявно предполагая, что притоки денежных средств по проекту Л во втором и третьем годах равны нулю. В принципе такое предположение нельзя считать абсолютно неправомочным, однако возможна и другая последовательность рассуждений.

Попробуем устранить временную несопоставимость проектов путем повтора реализации более короткого из них. Иными словами, предположим, что проект, А может быть реализован последовательно несколько раз. Каждая реализация обеспечит свой доход, а их сумма (в данном случае за три реализации) с учетом фактора времени, характеризующая изменение благосостояния владельцев вследствие принятия проекта, уже сопоставима с NPV проекта В. Такая логика представляется вполне разумной, поскольку позволяет устранить негативное влияние временного фактора ввиду разной продолжительности проектов. Следуя данной логике, мы по сути переходим от проекта А к некоторому условному проекту А', продолжающемуся три года и имеющему следующий вид:

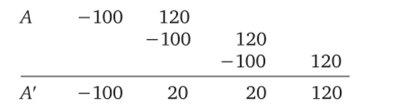
Проект А' имеет следующие значения критериев: NPV = = 24,9 млн руб., IRR = 20%. По критерию NPV проект А' уже предпочтительнее проекта В, поэтому выбор между исходными проектами, А и В в пользу последнего уже не представляется бесспорным.

Поскольку на практике необходимость сравнения проектов различной продолжительности возникает постоянно, разработаны специальные методы, позволяющие элиминировать влияние временного фактора: метод цепного повтора в рамках общего срока действия проектов; метод бесконечного цепного повтора сравниваемых проектов; метод эквивалентного аннуитета. Рассмотрим последовательно логику процедур каждого метода.

1. Метод цепного повтора в рамках общего срока действия проектов. Этот метод по сути и был продемонстрирован в начале раздела. Обычно продолжительность действия одного проекта может не быть кратной продолжительности другого. В этом случае рекомендуется находить наименьший общий срок действия проектов, в котором каждый из них может быть повторен целое число раз. Длина этого конечного общего срока находится с помощью наименьшего общего кратного. Последовательность действий при этом такова.

Пусть проекты А и В рассчитаны соответственно на i и j лет. В этом случае рекомендуется:

• • найти наименьшее общее кратное сроков действия проектов N = НОК (ij);
• • рассматривая каждый из проектов как повторяющийся, рассчитать с учетом фактора времени суммарный NPV проектов А и В, реализуемых необходимое число раз в течение периода N;
• • выбрать тот проект из исходных, для которого суммарный NPV повторяющегося потока имеет наибольшее значение.

Суммарный NPV повторяющегося потока находится по формуле.

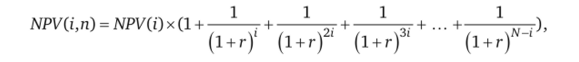
где NPV (г) — чистая текущая стоимость исходного проекта; i — продолжительность этого проекта; г — коэффициент дисконтирования в долях единицы; N — наименьшее общее кратное; п — число повторений исходного проекта (оно характеризует число слагаемых в скобках).

Пример В каждой из двух приведенных ниже ситуаций требуется выбрать наиболее предпочтительный проект (млн руб.), если цена капитала составляет 10%:

• 1) проект Л: —100; 50; 70, проект В: —100; 30; 40; 60;
• 2) проект С: -100; 50; 72, проект В: -100; 30; 40; 60.

Если рассчитать NPV для проектов А, В и С, то они составят соответственно: 3,30 млн руб., 5,4 млн руб., 4,96 млн руб. Непосредственному сравнению эти данные не поддаются, поэтому необходимо рассчитать NPV приведенных потоков. В обоих вариантах наименьшее общее кратное равно 6. В течение этого периода проекты Л и С могут быть повторены трижды, а проект В — дважды (рис. 5.14).

Из приведенной схемы видно, что в случае трехкратного повторения проекта, А суммарный NPV равен PV_A1 + PV_A2 + PV_A3 = 8,28 млн руб.:

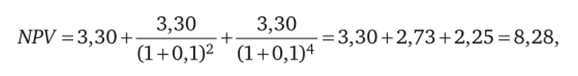
где 3,30 — текущая стоимость PV_M первой реализации проекта А; 2,73 — текущая стоимость PV_A2 второй реализации проекта А; 2,25 — текущая стоимость PV_A3 третьей реализации проекта А.

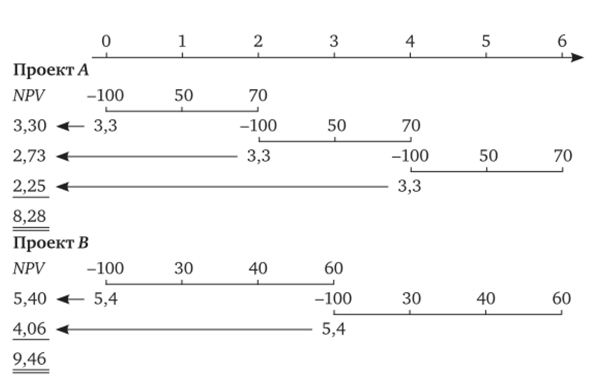
Рис. 5.14. Схема расчета NPV в рамках общего срока действия проектов Поскольку суммарный NPV в случае двукратной реализации проекта В больше (9,46 млн руб.), проект В является предпочтительным.

Если сделать аналогичные расчеты для варианта (2), получим, что суммарный NPV в случае трехкратного повторения проекта С составит 12,45 млн руб. (4,96 + 4,10 + 3,39). Таким образом, в этом варианте предпочтительным является проект С.

2. Метод бесконечного цепного повтора сравниваемых проектов. Рассмотренную в предыдущем разделе методику можно упростить. Так, если анализируется несколько проектов, существенно различающихся по продолжительности реализации, расчеты могут быть достаточно утомительными. Их можно уменьшить, если предположить, что каждый из анализируемых проектов может быть реализован неограниченное число раз. В этом случае при п -> °о число слагаемых в формуле расчета NPV (i, п) будет стремиться к бесконечности, а значение NPV (i, °°) может быть найдено по известной формуле для бесконечно убывающей геометрической прогрессии:

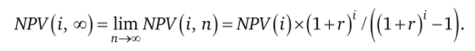
Из двух сравниваемых проектов проект, имеющий большее значение NPV (i, со) является предпочтительным.

Так, для рассмотренного примера:

вариант 1:

проект A: i = 2, поэтому NPV (2, °о) = 3,3×5,76 = 19,01 млн руб.;

проектВ: 7 = 3, поэтомуNPV (3, оо) = 5,4×4,02 = 21,71 млн руб.;

вариант 2:

проектВ: NPV (3, со) = 21,71 млн руб.,.

проект С: NPV{2, оо) = 28,57 млн руб.

Таким образом, получили те же самые результаты: в первом варианте предпочтительнее проектВ; во втором варианте предпочтительнее проект С.

• 3. Метод эквивалентного аннуитета. Этот метод в известной степени корреспондирует с методом бесконечного цепного повтора. Логика и последовательность вычислительных процедур таковы.
• 1. Рассчитывают NPV однократной реализации каждого проекта.
• 2. Для каждого проекта находят эквивалентный срочный аннуитет (ЕАА), текущая стоимость которого в точности равна NPV проекта, иными словами, рассчитывают величину аннуитетного платежа (А).
• 3. Предполагая, что найденный аннуитет может быть заменен бессрочным аннуитетом с той же самой величиной аннуитетного платежа, рассчитывают текущую стоимость бессрочно

ного аннуитета PV^a( <�"). Проект, имеющий большее значение PV^a(оо), является предпочтительным.

Для приведенного примера:

Вновь мы получили те же результаты: в первом случае предпочтительнее проект В; во втором случае — проект С. Легко заметить, что последнюю процедуру (расчет текущей стоимости бессрочного аннуитета) выполнять необязательно, т. е. можно принимать решение, сравнивая величины аннуитетного платежа ЕАА.

Методам, основанным на повторе исходных проектов, присуща определенная условность, заключающаяся в молчаливом распространении исходных условий на будущее, что, естественно, не всегда корректно. Во-первых, далеко не всегда можно сделать точную оценку продолжительности исходного проекта. Во-вторых, не очевидно, что проект будет повторяться какое-то конкретное число раз, особенно если он сам по себе достаточно продолжителен. В-третьих, условия его реализации в случае повтора могут измениться (это касается как размера инвестиций, так и величины прогнозируемых чистых доходов). В-четвертых, расчеты во всех рассмотренных методах абсолютно формализованны, при этом не учитываются различные факторы, которые являются либо неформализуемыми, либо имеют общеэкономическую природу (инфляция, научно-технический прогресс, изменение технологий, заложенных в основу исходного проекта, и др.).