Цилиндр (граничные условия первого рода)

Эффективность совместного использования методов Канторовича и Бубнова —Галеркина рассмотрим также на примере решения нестационарной задачи теплопроводности для неограниченного цилиндра при симметричных граничных условиях первого рода. Математическая постановка задачи имеет вид.

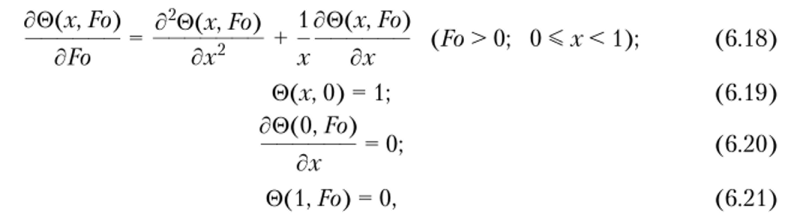
где х = т|/8 — безразмерная радиальная координата; 8 — радиус цилиндра. Остальные обозначения те же, что и в параграфе 6.1.

Решение задачи (6.18)—(6.21), следуя методу Канторовича, разыскивается в виде.

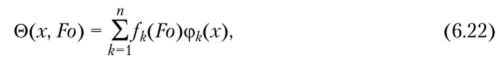
где fit (Fo) — неизвестные функции времени; ср/_;(.т) — координатные функции, определяемые по формуле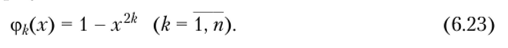

Соотношение (6.22) благодаря принятой конструкции координатных функций точно удовлетворяет граничным условиям (6.20), (6.21). Для нахождения неизвестных функций времени/ДДо) составляется невязка уравнения (6.18) и требуется ортогональность невязки ко всем координатным функциям: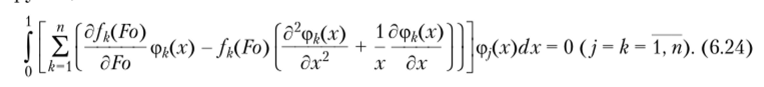

Определяя интегралы в (6.24), относительно неизвестных функций времени приходим к системе обыкновенных дифференциальных уравнений первого порядка вида (6.10), где.

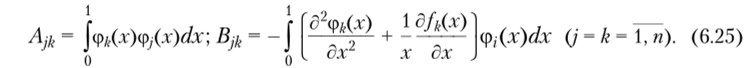
Частные решения системы уравнений (6.10) разыскиваются в виде (6.11).

Подставляя (6.11) в (6.10), получим систему однородных алгебраических уравнений вида (6.12). Раскрывая определитель этой системы относительно р, получим алгебраический полином п-й степени.

Постоянные Q, находятся из начального условия (6.19) путем решения системы алгебраических линейных уравнений вида (6.17). Из решения этой системы, например, для п = 6 находим значения постоянных.

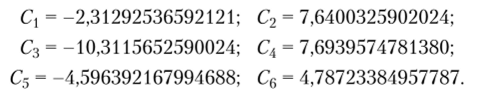
После нахождения С окончательное решение задачи (6.18)—(6.21) в замкнутом виде находится из (6.22).

На графиках рис. 6.5 представлены результаты расчетов безразмерной температуры по формуле (6.22) в шестом приближении в сравнении с точным решением [49]. Собственные числа для трех и шести приближений, а также точные их значения представлены в табл. 6.2.

Анализ полученных результатов показывает, что с увеличением числа приближений собственные числа с низшими порядковыми номерами всякий раз уточняются.

Анализируя графики рис. 6.5, можно заметить, что в шестом приближении безразмерные температуры в диапазоне 0,005 < Fo < °° практически совпадают с их точными значениями.

Изменения невязок уравнения (6.18) и начального условия (6.19) представлены на графиках рис. 6.6—6.8. Их анализ позволяет заключить, что максимальная невязка уравнения (6.18) имеет место в точке х = 1. Максимальная невязка начального условия (см. рис. 6.8) также имеет место в точке х = 1 и равна е = -1.

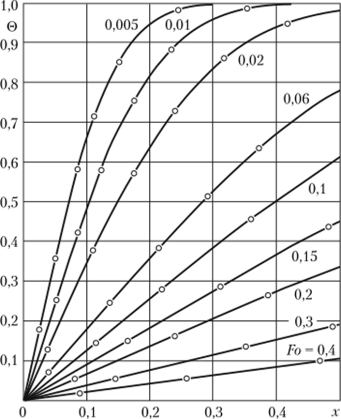
Рис. 65. Графики распределения относительной избыточной температуры в цилиндре:

—расчет по формуле (6.22) (шестое приближение); ° — точное решение [49).

Таблица 6.2

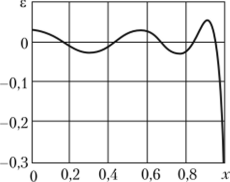
Рис. 6.6. Изменение невязки е уравнения (6.18) при и = 6 (Fo = 0,1).

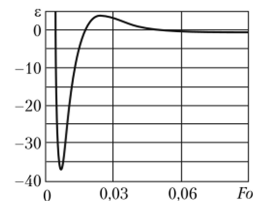
Рис. 6.7. Изменение невязки е уравнения (6.18) во времени для и = 6 в точкех = 1.

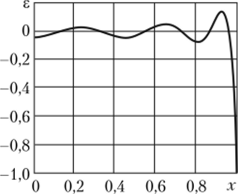
Рис. 6.8. Изменение невязки е начального условия при п = 6 (~Fo = 0).

Математическая постановка нестационарной задачи теплопроводности для шара при симметричных граничных условиях первого рода имеет вид.

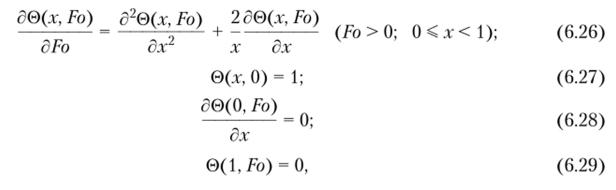
где обозначения те же, что и в задаче параграфа 6.2.

Решение задачи (6.26)—(6.29), следуя методу Канторовича, разыскивается в виде (6.22), где fk (Fo) — неизвестные функции времени; срДх) — координатные функции, определяемые по формуле (6.23).

Соотношение (6.22) точно удовлетворяет граничным условиям (6.28), (6.29). Для нахождения неизвестных функций времениfk (Fo) составляется невязка уравнения (6.26) и требуется ортогональность невязки ко всем координатным функциям:

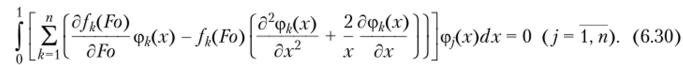
Определяя интегралы в (6.30), относительно неизвестных функций времени приходим к системе обыкновенных дифференциальных уравнений первого порядка вида (6.10). Последовательность дальнейшего решения задачи совпадает с решениями для пластины и цилиндра.

Коэффициенты Q для шести приближений в данном случае будут равны.

После нахождения С* окончательное решение задачи (6.26)—(6.29) в замкнутом виде находится из (6.22).

На графиках рис. 6.9 представлены результаты расчетов безразмерной температуры по формуле (6.22) в шестом приближении в сравнении с точным решением [49]. Собственные числа для трех и шести приближений, а также точные их значения [49] представлены в табл. 6.3.

Таблица 63

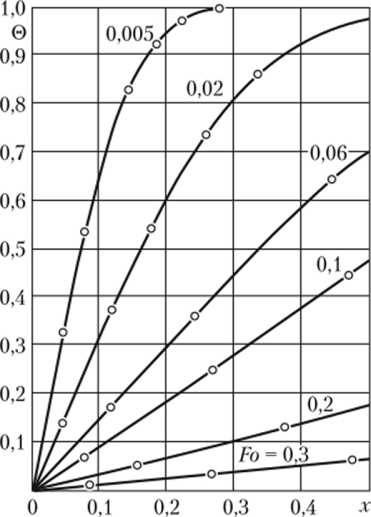
Рис. 6.9. Графики распределения относительной избыточной температуры

в шаре:

—расчет по формуле (6.22) (шестое приближение); о — точное решение [49].

Анализируя графики рис. 6.9, можно заметить, что в шестом приближении безразмерные температуры в диапазоне 0,005 < Fo < °° практически совпадают с их точными значениями.

Изменения невязок уравнения (6.26) и начального условия (6.27) представлены на графиках рис. 6.10—6.12.

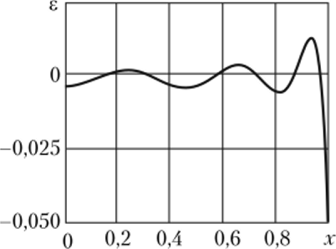
Рис. 6.10. Изменение невязки е уравнения (6.26) при п = 6 (шесть приближений) (Fo = 0,05).

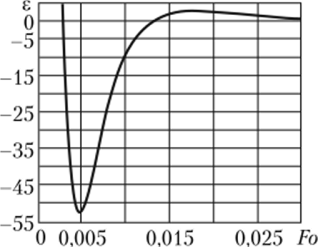
Рис. 6.11. Изменение невязки е уравнения (6.26) во времени для п = 6 в точке х = 1.

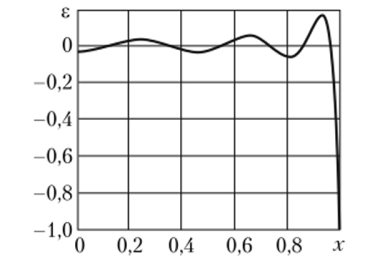
Рис. 6.12. Изменение невязки е начального условия при п = 6 (Fo = 0).

Задачи теплопроводности при неоднородных и несимметричных граничных условиях третьего рода представляют большой практический интерес для изучения теплопередачи в системе среда — стенка — среда. Теоретические исследования подобных задач для пластины, полого цилиндра и сферической оболочки приводят к сложным математическим преобразованиям, а температурные поля в этих телах выражаются громоздкими функциональными рядами. Все это затрудняет внедрение полученных решений в практику инженерных расчетов.

Для решения таких задач достаточно эффективными оказываются приближенные аналитические методы (вариационные, взвешенных невязок, коллокаций и др.). Ниже будет рассмотрена последовательность совместного применения метода Канторовича и ортогонального метода Бубнова — Галеркина применительно к решению задачи теплопроводности для бесконечной пластины при несимметричных граничных условиях третьего рода. Математическая постановка задачи имеет вид.

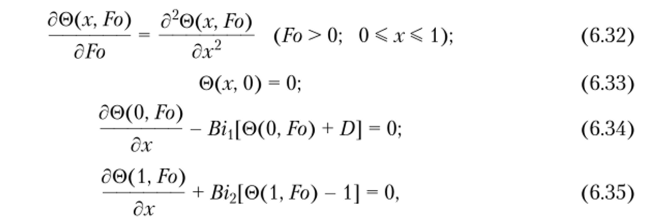
где 0 = (ГГ₀)/(Г₂ - Г₀); D = (Г₀ — Т_Х)/(Т₂ — Т_{); Вц = сцбД; Bi₂ = а₂5Д; 7*1, Т₂ — температуры сред; Tq — начальная температура; Fo = ах/Б².

Решение задачи (6.32)—(6.35) представляется в виде суммы двух функций: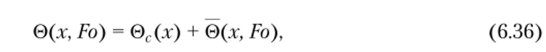

где ®_с(^х) ~ решение стационарной задачи теплопроводности с неоднородными граничными условиями (6.34), (6.35); 0(x, Fo) — решение нестационарной задачи с соответствующими однородными граничными условиями. Решение стационарной задачи принимается в виде.

где F и F₂ — неизвестные коэффициенты, определяемые из граничных условий (6.34), (6.35).Формулы для них будут [83] иметь вид.

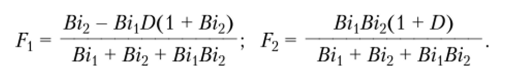
Математическая постановка задачи для функции 0(х, Fo) имеет вид.

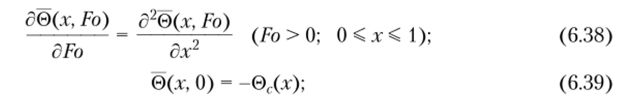
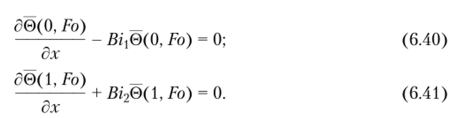
Решение задачи (6.38)—(6.41), следуя ортогональному методу Канторовича, разыскивается в виде.

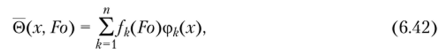
где fk (Fo) — неизвестные функции времени; ф/,(х) — координатные функции, определяемые таким путем, чтобы точно удовлетворялись граничные условия (6.40), (6.41).

Координатная функция первого приближения фДж) находится, но формуле.

где коэффициенты Ф] и Ф₂, определяемые из граничных условий (6.40), (6.41), имеют вид [83].

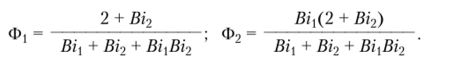
Координатные функции последующих приближений фДл^-) (к = 2, п) определяются по формуле.

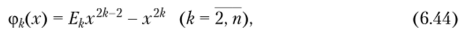
где коэффициенты ?), (k = 2, и) в каждом приближении находятся из граничных условий (6.40), (6.41). Общая формула для них будет иметь вид.

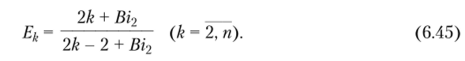
Соотношение (6.42) при использовании координатных функций вида (6.43), (6.44) в любом приближении точно удовлетворяет граничным условиям (6.40), (6.41). Для нахождения неизвестных функций времени fu{Fo), следуя методу Бубнова—Галеркина, составляется невязка уравнения (6.38) и требуется ортогональность невязки ко всем координатным функциям:

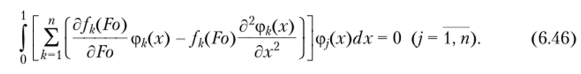
Определяя интегралы в (6.46), относительно неизвестных функций времени приходим к однородной системе обыкновенных дифференциальных уравнений первого порядка вида (6.10).

Частные решения системы уравнений (3.10) разыскиваются в виде.

где Djhij = k = 1, п), р — неизвестные постоянные.

Подставляя (6.47) в (6.10), получим систему однородных алгебраических уравнений вида (6.12). Раскрывая определитель этой системы, относи;

тельно р получим алгебраический полином п-й степени. При Вц = 2 и Bi₂ = 3 собственные числа для трех, пяти и семи приближений в сравнении с точными их значениями [17] представлены в табл. 6.4.

Точные значения собственных чисел определялись из уравнения 1171.

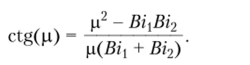
Формула для неизвестных функций времени принимает вид.

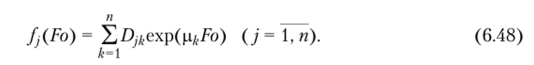
Соотношение (6.48) является частным решением системы уравнений (6.10). Для нахождения общего решения этой системы умножим частное решение, отвечающее корню p_t, на произвольную постоянную С, отвечающее р₂ — на С₂ и т. д. Тогда решение (6.42) примет вид.

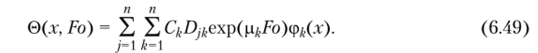
Постоянные Q находятся из начального условия (6.33). Для этого составляется его невязка и требуется ортогональность невязки ко всем координатным функциям:

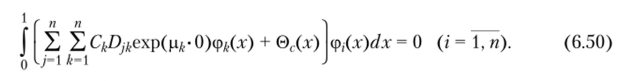
Соотношение (6.50) после определения интегралов относительно коэффициентов С/. (k⁼ 1. п) представляет систему алгебраических линейных уравнений. В седьмом приближении (и = 7) получены следующие их значения:

После определения Q окончательное решение задачи (6.32)—(6.35) в замкнутом виде находится из (6.36).

На графиках рис. 6.13 представлены результаты расчетов безразмерной температуры 0(х, Fo) по формуле (6.36) в седьмом приближении в сравне;

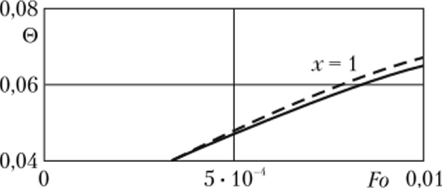
Рис. 6.13. Графики распределения относительной избыточной температуры.

для пластины:

—расчет по формуле (б.Зб) (седьмое приближение);——точное решение [ 171.

нии с точным решением [17] для Bi_{ = 2, Bi₂ = 3. Анализируя эти результаты, можно отметить, что полученные в настоящей работе безразмерные температуры при Fo > 0,002 практически совпадают с их точными значениями.

Анализируя невязку 8 уравнения (6.32) по координате х при Fo = 0,2 (рис. 6.14), можно заметить, что максимальное значение 8 принимает в граничных точкахх = 0 их = 1. Анализ изменения невязки уравнения (6.32) во времени в точках х = 0 (рис. 6.16) и х = 1 (рис. 6.15) показывает, что максимальная невязка имеет место в начальные моменты времени. С увеличением времени навязка уменьшается, асимптотически приближаясь к нулю при больших значениях числа Фурье.

Максимальная невязка начального условия (6.33) имеет место при х = 1 (рис. 6.17). С увеличением числа приближений невязка начального условия (так же, как и невязка уравнения (6.32)) уменьшается.

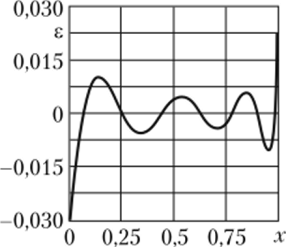
Рис. 6.14. Изменение невязки 8 уравнения (6.32) при п = 7 (семь приближений) (Fo = 0,2).

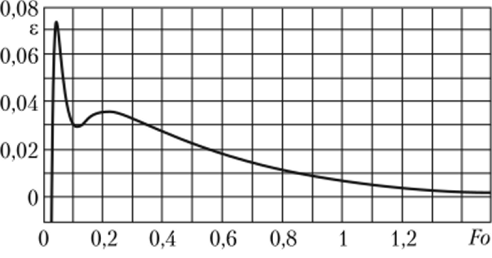
Рис. 6.15. Изменение невязки 8 уравнения (6.32) во времени при п = 7 в точке х = 1.

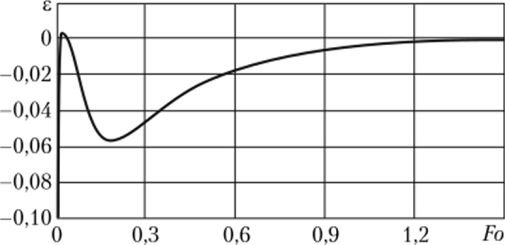
Рис. 6.16. Изменение невязки е уравнения (6.32) во времени при п = 7 в точке л: = 0.

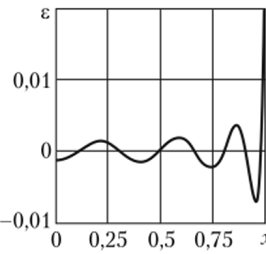
Рис. 6.17. Изменение невязки 8 начального условия при п = 7 (Fo = 0).