Выборочные точечные характеристики (статистики)

Выборки описываются с помощью характеристических чисел — так называемых статистик, которые служат для оценки параметров законов распределений при исследовании свойств случайных величин. Статистика, определяемая одним числом, называется точечной.

Точечная оценка, математическое ожидание которой равно оцениваемому параметру генеральной совокупности, называется.

несмещенной, в противном случае — смещенной. Статистики сами являются случайными величинами, так как описываемая ими выборка является случайным набором чисел.

Средние определяют центр распределения случайной величины X, около которого группируется большая ее часть. Средние имеют ту же размерность, что и величина X. Характеристиками среднего являются следующие величины.

Выборочное среднее, или среднее арифметическое,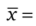

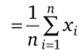 — наиболее распространенный вид средней, является несмещенной оценкой математического ожидания р. Характеризует расположение центра распределения.

Среднее квадратическое 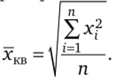Среднее кубическое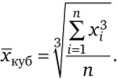

Среднее геометрическое 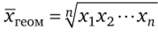. Этой средней пользуются в расчетах среднегодовых темпов роста, когда рассматриваются не абсолютные приросты, а отношения двух статистических величин.

Медиана (Me) — значение среднего элемента вариационного ряда.

Медиана делит вариационный ряд на две равные по объему части: 50% всех элементов вариационного ряда меньше медианы, а 50% — больше нее.

Для теоретического распределения медиана соответствует квантилю уровня, а = 0,5 (пятидесятому процентилю), т. е. равновероятно, что случайная величина окажется больше или меньше медианы: Р (Х Me) = 0,5.

Медиана находит применение, например, в маркетинговой деятельности при выборе базы снабжения с целью минимизации транспортных расходов.

Мода (Мо) — значение x_(i), которое наблюдается наибольшее число раз. На графике теоретической кривой распределения f (x)

мода является абсциссой точки максимума, для которой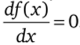

Мода часто используется при определении размеров одежды и обуви, которые пользуются широким покупательским спросом [17]. Она выявляет наиболее часто встречающийся тип покупателя.

Средние величины являются закономерным результатом воздействия главных факторов, влияние прочих факторов увеличивает степень рассеяния случайной величины.

Характеристиками рассеяния случайной величины X около центра распределения х являются следующие показатели.

Выборочная дисперсия 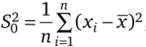, является смещенной оценкой дисперсии, так как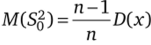

Выборочное среднее квадратичное (стандартное) отклонение

So ⁼ [Щ-

Величины Sq, S₀ характеризуют степень рассеяния около центра распределения.

Для быстрого ручного счета используют формулу.

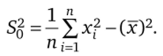
Смещение сказывается при небольшом объеме выборки (п < 50), в этом случае используют несмещенную оценку.

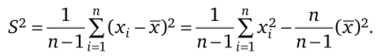
При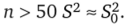

Коэффициент вариации V-S/x 100%. Если V > 40%, то разброс значений признака X в исследуемой выборке считается значительным. Если V > 100%, то можно сделать вывод, что наблюдения неоднородны.

Коэффициент вариации используют для сравнения двух или более выборок, отличающихся единицами измерения. Когда наблюдения колеблются около нуля, им не рекомендуется пользоваться в качестве меры рассеяния. В этом случае значения S и х близки к нулю и незначительное изменение того или другого может привести к резкому изменению коэффициента вариации.

Размах варьирования R = x_max — x_min из-за простоты вычисления часто используют как характеристику рассеяния при контроле качества в промышленности, поскольку в этом случае изменения контролируемого параметра х обычно происходят постепенно и равномерно и вариационный ряд не имеет случайных выбросов.

Межквартилъный размах х_{0 75} — х_{0 2}5, равный разности значений верхней и нижней квартилей, используется в экономических и социальных задачах, когда распределения частот имеют сильные выбросы («хвосты») или скошенность (слишком большие или малые выпадающие значения).

Скошенность распределения/(х), его несимметричность характеризует коэффициент асимметрии 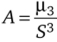, где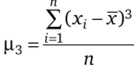

Если в вариационном ряду преобладают наблюдения, меньшие х, то асимметрия левосторонняя, при этом А < 0, Мо > х; при А > О асимметрия правосторонняя, в этом случае Мо < х (рис. 7.6).

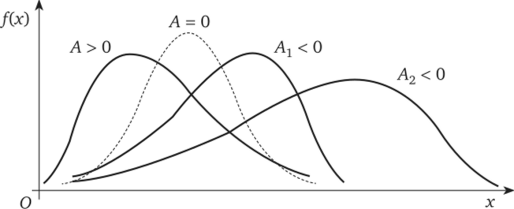
Рис. 7.6. Кривые распределений с различной асимметрией.

Несимметричность возникает под влиянием причин, действующих в одном направлении. Например, ряд распределения длины волокна китайского хлопка, представляющего почти естественное состояние, имеет незначительную отрицательную асимметрию. Под воздействием селекции, направленной в сторону увеличения длины волокна, абсолютная величина отрицательной асимметрии возрастает: для русского хлопка американских семян А₁ — -0,453, для русского хлопка египетских семян А₂ = -0,725 (см. рис. 7.6) [23].

Для симметричного распределения х = Мо = Me.

Большинство данных, собираемых в промышленности для контроля, например, размеров деталей, распределены симметрично. Скошенность распределений характерна для данных в социологии. Например, при сравнении доходов различных слоев населения наблюдаются перекосы в пользу бедных или богатых. В этом случае важно получить информацию о соотношении средних величин х, Мо, Me.

Эксцесс, или коэффициент крутости, 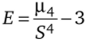, где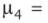

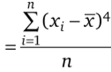-, характеризует отклонение от крутовершинности нормальной кривой, для которой? = 0. При Е < 0 кривые по сравнению с нормальной менее крутые, имеют плоскую вершину и выраженные хвосты; при Е > 0 кривые крутые и островершинные (рис. 7.7).

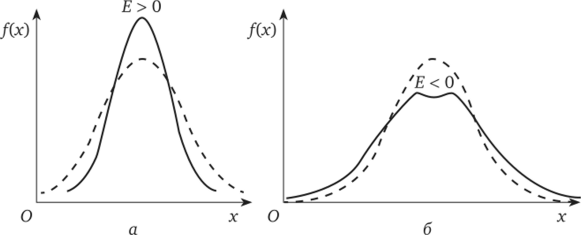
Рис. 7.7. Кривые распределений с положительным (а) и отрицательным (б) эксцессом.

Асимметрия и эксцесс могут использоваться для подбора закона распределения. Так как для любого нормального распределения асимметрия и эксцесс равны нулю, то распределение считается близким к нормальному, если выборочные |А| < 0,1 и |?| 0,5 или |?| > 0,5 говорят о том, что распределение соответственно является сильно асимметричным или значительно отклоняется от нормального.

Появление двухвершинной или асимметричной кривой говорит о неоднородном, разнотипном составе выборки, который может быть вызван нарушением нормальных параметров технологического процесса или условий производства.