Алгебры с делением конечного ранга над полем действительных чисел

Поле действительных чисел (М, +, •), поле комплексных чисел (С, +, •) и тело кватернионов (Н, +, •) являются векторными пространствами над полем действительных чисел. Общий взгляд на системы действительных, комплексных чисел и кватернионов порождает следующее определение.

Определение 4.17. Алгеброй с делением над полем Р (в частности, над полем действительных чисел R) называется тело (А, +, •}, которое одновременно является векторным пространством над полем Р, причем для любого скаляра а е Р и любых векторов а, (3 е А (аа) • Р = а (а • (3) = а • (а (3). Размерность векторного пространства, А над полем Р (количество векторов базиса) называется рангом алгебры. Если ранг алгебры конечен, то она называется конечномерной.

Очевидно, поле действительных чисел, поле комплексных чисел и тело кватернионов являются конечномерными алгебрами с делением над полем действительных чисел соответственно рангов 1, 2 и 4 (их базисы, соответственно, {1}, {1, г} и {1, i, j, к}. Есть ли другие примеры? Отвечает на этот вопрос следующая теорема.

Теорема 4.20 (Фробениуса). Система (А, +, •) является алгеброй с делением конечного ранга над полем действительных чисел тогда и только тогда, когда она является либо полем действительных чисел, либо полем комплексных чисел, либо телом кватернионов.

Доказательство. Ввиду сказанного выше остается доказать, что если система (А, +, ?) является алгеброй с делением конечного ранга над полем действительных чисел, то она является либо полем действительных чисел, либо полем комплексных чисел, либо телом кватернионов. Доказательство этого разобьем на ряд лемм.

Лемма 4.7. Алгебра с делением (А, +, •) над полем Р содержит подполе, изоморфное полю Р. С точностью до изоморфизма можно считать, что поле Р содержится в А.

Доказательство. Пусть е — единица алгебры (А, +, •). Очевидно, множество F = {ае, а е Р} является подполем в А. Для любого ае Р определим /(ае) = а. Легко доказать, что/является изоморфизмом подполя F на поле Р. Отождествляя элемент ае е F с элементом а е Р, можно считать, что РсА. Лемма доказана.

Следствие. Если алгебра с делением (А, +, •) над полем R имеет ранг 1, то она является полем действительных чисел.

Доказательство. По лемме 4.7 R с А, а так как ранг алгебры Л равен 1, то линейно независимая над R система {1} является базисом в А. Это значит, что для любого а е А существует число qe К, такое что, а = al = а е R. Следовательно, А = R.

Лемма 4.8. Всякий ненулевой элемент, а алгебры с делением (А, +, •) конечного ранга над полем Р является корнем некоторого многочлена ср (х) е Р[х], неприводимого над этим полем.

Доказательство. Пусть ранг алгебры (А, +, •) равен п. Известно, что в п-мерном векторном пространстве всякие п + 1 векторов линейно зависимы. Следовательно, для любого О Ф Ф а е А система векторов {1 = а⁰, а, а², …, а^п} линейно зависима. Это значит, что существуют элементы поля а₀, а_ь а₂, …, а_п, среди которых есть элементы, отличные от нуля, такие что а₀ + а_га + а₂а² + … + а_па^п = 0. Но это и означает, что, а является корнем многочлена а₀ + арс + аух² + … + a_tTxⁿ е Р[х]. Из всех многочленов с коэффициентами из Р, имеющих корень а, выберем тот, который имеет наименьшую степень, пусть это будет ф (х). Тогда степень ф (х) не меньше 1. Предположим, что этот многочлен приводим над полем Р, пусть ф (х) = ф^х) • ф₂(х), где Ф₂(х), ф₂(х) g Р[х], и степени сомножителей меньше степени многочлена ф (х). Тогда ф₂(а) • ф₂(а) = ф (а) = 0, а так как тело не имеет делителей нуля, то ф₂(а) = 0 или ф₂(а) = 0. Таким образом, а является корнем одного из многочленов ф_а(х) или ф₂(х), что противоречит минимальности степени многочлена ф (х). Следовательно, многочлен ф (х) неприводим над полем Р. Лемма доказана.

Лемма 4.9. Алгебра с делением (А, +, •) над полем комплексных чисел С изоморфна этому полю и с точностью до изоморфизма можно считать, что, А = С.

Доказательство. По лемме 4.7 алгебра с делением (Л, +, •) над полем С содержит поле С. По лемме 4.8 всякий ненулевой элемент а е А является корнем некоторого многочлена ф (х) е е С[х], неприводимого над полем С. Известно, что неприводимыми над полем комплексных чисел являются лишь многочлены первой степени. Следовательно, ф (х) = ах + Ь при некоторых а, b е Сиа Ф 0. Таким образом, аа + b = ф (а) = 0, откуда, а = -Ыа е С. Следовательно, А = С. Лемма доказана.

Лемма 4.10. Если алгебра с делением (А, +, •) над полем R имеет ранг п > 1, то она содержит подполе, изоморфное полю комплексных чисел С, и с точностью до изоморфизма можно считать, что С с А.

Доказательство. По лемме 4.7 алгебра Л содержит поле R. Так как поле R является одномерным векторным пространством над полем R, т. е. над самим собой (с базисом {1}), а ранг Л над полем R равен п > 1, то, А A R. Пусть, а е AR. По лемме 4.8 а является корнем некоторого многочлена cp (x) е R[x], неприводимого над полем R. Известно, что неприводимыми над полем действительных чисел являются лишь многочлены первой степени и многочлены второй степени с отрицательными дискриминантами. Если предположить, что степень ср (х) равна единице и ф (х) =ах + Ь, где a, b е R и а Ф 0, то получаем аа + Ь = ф (а) = О, откуда, а = b/a е R, что противоречит выбору элемента а. Следовательно, степень ф (х) равна двум и ф (х) = ах² + Ьх + с при некоторых а, Ь, с е R и, а Ф 0, причем дискриминант b² — 4ас < 0. Но тогда 4ас — Ь² > 0 и существует del, такое что d² = 4 ас — Ь². Поскольку аа² + Ьа + с = ф (а) = 0, то.

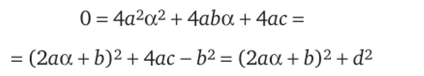
(2аа + Ъ)² «——-'•.

Обозначим i = ^^{аа +} _; тогда i² = -1. Вместе с тем С = R + Ш = d

= {а + bi a, b е R} является полем комплексных чисел, содержащимся в А. Лемма доказана.

Следствие. Если алгебра с делением (А, +, •} над полем R имеет ранг 2, то она является полем комплексных чисел.

Доказательство. По лемме 4.10 С с А. Система векторов {1, i} линейно независима над R, а так как ранг, А над полем R по условию равен 2, то эта система является базисом в А. Следовательно, всякий элемент, а е, А является линейной комбинацией этих базисных векторов: а = а • 1 + Ъ? i для некоторых а, b е R. Таким образом, А = С.

Лемма 4.11. Если алгебра с делением (А, +, •) над полем R имеет ранг п > 2, то она является телом кватернионов.

Доказательство. По лемме 4.10 С с А, где С = R + Ш. Рассмотрим множества U = {а е, А | ai = ia} и V = {(3 е, А | (3i = -i'P}. Легко видеть, что для любого у е А имеем у — iyi е U, а у + iyi е

е V и у = — iyi) + ^(у + iyi) eU + V. Следовательно, A = U + V.

Если предположить, что S е U nV, то 6 е U, откуда Ы = г§, и 8 е V, откуда 6 г = -гб. Следовательно, i5 = -t8, откуда 2i5 = 0, а так как тело не содержит делителей нуля, то б = 0. Таким образом, U п V = {0}.

Выясним строение подмножеств U и V. Легко видеть, что UuV являются векторными пространствами над полем Е, причем U является алгеброй с делением над полем С и по лемме 4.9 U — С.

По условию, ранг Л равен п > 2, а так как ранг С над полем Е равен двум, то V — ненулевое векторное пространство над полем Е и существует О Ф (3 е V. По лемме 4.8 (3 является корнем некоторого многочлена ср (лг) е Е[х], неприводимого над полем Е. Поскольку неприводимыми над полем Е являются лишь многочлены первой степени и второй степени с отрицательными дискриминантами, то степень ср (лг) равна либо единице, либо двум. Рассмотрим оба случая.

В первом случае (р (х) =ах + Ь, где a, b е Е и а Ф 0. Поскольку а (3 + b — ф ((3) = 0, то (3 = — е Е с С = U. Следовательно, (3 е U п.

а

n V = {0}, откуда |3 = 0, что противоречит предположению. Во втором случае ф (х) = ах² + Ьх + с, где a, b, с е Е, а А 0 и дискриминант Ь² — 4ас < 0. Поскольку Р — корень многочлена ф (х), то 0 = ф (Р) = аР² + bp + с. Заметим, что р² е U, и если предпо;

ttP² + с ложить, что b Ф 0, то Р = ——е U.

Ъ

С другой стороны, Р² g V. Следовательно, Ре U nV = {0}, откуда Р = 0, что снова противоречит нашему предположению.

Q

Таким образом, Ъ = 0 и мы получаем аР² + с = 0, откуда р² = —.

а

с

Так как дискриминант Ь² — 4ас < 0, то 4ас >Ь²- 0, откуда — > 0.

а

с

Следовательно, существует d е Е, такое что — = d². Таким обра;

а

_п Q2 3.

зом, Р² = -d², откуда^- = -1. Обозначив j = —, получим j² = -1. d² d.

Докажем, что V = С/. Так как; е V, то (if)i = i (ji) = = -i²j =j,

i (y) = i²j = -j, откуда (ij)i = -i (ij), значит, ij e V. Но тогда для любого комплексного числа а + Ы получаем (а + bi)j = aj + bij е V. Таким образом, Сj с V. Обратно, для любого Р е V получаем (Р/) i = РО’О = Р (-У) = — CPOj = -HP); = i (P;), откуда Р; е U = С и, следовательно, Р е Cj. Таким образом, А = С + С/.

Обозначим к = ij. Легко проверить, что к² = ijk = -1. Всякий элемент h е А представим в виде h = Z_x + при некоторых Zj, Z₂ е С. Запишем эти комплексные числа в алгебраической форме: Z₁ = a + bi, Z₂ = c + di. Тогда h = (a + bi) + (с + di)j = a + b + + cj + dij = a + bi + cj + dk. В этой записи мы узнаем кватернион. Следовательно, система (А, +, •) является телом кватернионов.

Вместе с тем теорема Фробениуса доказана.

Таким образом, можно сделать следующие выводы.

• 1. Поле действительных чисел — это единственная алгебра с делением над полем R ранга 1.
• 2. Поле комплексных чисел — это единственная коммутативная и ассоциативная алгебра с делением над полем М ранга п > 1.
• 3. Тело кватернионов — это единственная ассоциативная некоммутативная алгебра с делением над полем R конечного ранга.

По поводу дальнейших расширений числовых множеств см. работу [6].

Заметим, что в соответствии с «Математической энциклопедией»^[1] кольцом называется множество К с двумя бинарными операциями, которые называются сложением и умножением, причем К относительно сложения является абелевой группой, называемой аддитивной группой кольца, и умножение дистрибутивно относительно сложения: аф + с) = ab + ас и ф + с) а = = Ьа + са для любых а, Ь, с е К. В этом случае кольцо, определенное ранее, называется ассоциативным кольцом. Кольцом с делением называется кольцо К (необязательно ассоциативное), в котором для любых а, ЬеК, где а ^ 0, разрешимы уравнения ах = Ъ иуа = Ь. Если решения этих уравнений определены однозначно, то такое кольцо с делением называется квазителом.

• [1] Математическая энциклопедия. М.: Советская энциклопедия, 1979.С. 959.