Гетероскедастичность пространственной выборки

Как уже отмечалось выше, равенство дисперсий возмущений (ошибок) рсгрессиии е, (гомоскедастичность) является существенным условием линейной классической регрессионной модели множественной регрессии, записываемым в виде ^_с=а²?".

Однако на практике это условие нередко нарушается, и мы имеем дело с гетероскедастичностью модели.

Предположим, что необходимо изучить зависимость размера оплаты труда К (в уел. ден. ед.) сотрудников фирмы от разряда X, принимающего значения от 1 до 10. Получены п = 100 пар наблюдений (x_h у,). График зависимости переменной Кот номеров наблюдений, упорядоченных по возрастанию уровня значений объясняющей переменной X, показан на рис. 7.1.

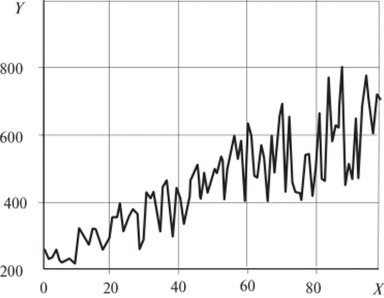
Рис. 7.1.

Из рис. 7.1 отчетливо видно, что вариация размера оплаты труда сотрудников высоких уровней значительно превосходит его вариацию для сотрудников низких уровней. Следовательно, мы вправе предположить, что регрессионная модель получится гетероскедастичной, и условие ?_е=а²?" нс выполняется.

Мы еще вернемся к этому примеру, а пока обсудим, к каким последствиям приводит гете роскедастич ность.

Предположим, что для оценки регрессионной модели У по Х,.₉ Х_п мы применили обычный метод наименьших квадратов и нашли оценку b параметра р по формуле (4.8). Тогда с учетом (4.12) будем иметь.

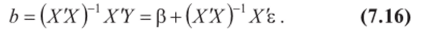
Как было отмечено в § 7.1, b — несмещенная и состоятельная оценка параметра р для обобщенной линейной модели множественной регрессии; следовательно, и в частном случае, когда модель гетероскедастична, оценка b — несмещенная и состоятельная. Эти свойства оценки b легко усматриваются из (7.16), если учесть, что Л/(е)=0.

Таким образом, для определения неизвестных (прогнозных) значений зависимой переменной обычный метод наименьших квадратов, вообще говоря, применим и для гетсроскедастичной модели.

Так, в нашем примере изучения зависимости размера оплаты Y от разряда X сотрудников фирмы регрессионная модель Y по X примет вид:

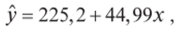
которая вполне может быть использована для практических приложений.

Однако результаты, связанные с анализом точности модели, оценкой значимости и построением интервальных оценок ее коэффициентов, оказываются непригодными.

В самом деле, при построении /- и /^статистик, которые служат инструментом для проверки (тестирования) гипотез, существенное значение имеют оценки дисперсий и ковариаций параметров р, — (/= 1,…, я), т. е. ковариационная матрица? _ь. Между тем, если модель не является классической, т. е. ковариационная матрица вектора возмущений? _е = Q * ст²Е_п, то, как показано в § 7.1, ковариационная матрица вектора оценок параметров ^ь={Х'ХУ'Х'ПХ{Х'ХУ' (7.2) существенно отличается от полученной для классической модели ^,= <7² (.XX)'¹ (7.3). А значит, использование матрицы Yjb (7.2) для оценки точности регрессионной модели (7.1) может привести к неверным выводам.

Напомним также (§ 7.1), что оценка b (7.16), оставаясь несмещенной и состоятельной, не будет оптимальной в смысле теоремы Гаусса—Маркова, т. е. наиболее эффективной. Это означает, что при небольших выборках мы рискуем получить оценку b, существенно отличающуюся от истинного параметра р.