Алгоритмические основы компьютерной графики. 
Растровые алгоритмы, определение видимости, закрашивание

Помимо ранее рассмотренной работы с матрицами и векторами (которые фактически являются частью линейной алгебры), в компьютерной графике существует целый ряд своих алгоритмов и методов. В этой главе рассмотрим основные алгоритмы для решения следующих задач — растеризации геометрических примитивов, определения видимости при проектировании на плоскость, определения освещенности и закрашивания.

Растровые алгоритмы

Практически вся современная компьютерная графика является растровой, т. е. она строит двухмерные изображения, состоящие из отдельных пикселов. Каждый пиксел обладает своими координатами и своим цветом. Все пикселы расположены на растровой сетке, которая представляет собой множество точек на плоскости с целочисленными координатами (рис. 7.1).

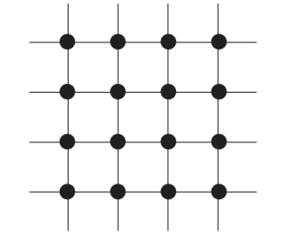
Рис. 7.1. Растровая сетка.

Обычно мы работаем с трехмерными объектами, заданными своими координатами. Все операции задаются именно над этими объектами, и на определенном этапе возникает задача растеризации — перевода идеальных математических объектов (таких как треугольники) в набор пикселов.

При растеризации объектов возникает следующее естественное требование: если исходный объект является связным (т.е. две его любые точки можно соединить линией, целиком лежащей в данном объекте), то и его растровое представление тоже должно быть связным в некотором смысле. Говоря о связности на растровой сетке, обычно рассматривают следующие два определения связности — 4-связность и 8-связностъ.

Пикселы (х₀ у₀) и (х_х у_х) являются 4-связными (соседними) тогда и только тогда, когда выполнено неравенство |^-.г₀| + +у₀ — г/, | < 1 (рис. 7.2, слева). Таким образом, если два пиксела являются 4-связными, то они могут отличаться не более чем в одной координате и не более чем на единицу.

Более мягким требованием является 8-связность: пикселы (х₀ у₀) и {х_х у_{) являются 8-связными, если выполнены следующие два неравенства: |.r, -х₀| < 1, |у_{ -у₍₎| < 1 (рис. 7.2, справа).

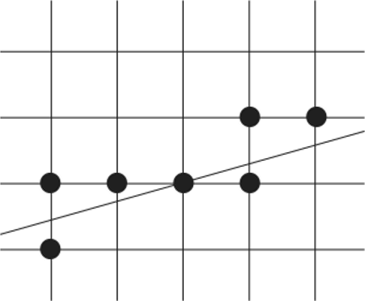
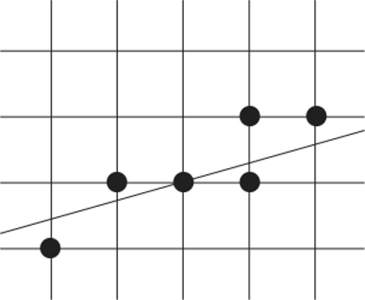
Рис. 7.2. Связность пикселов.

Отметим, что если два пиксела 4-связны, то они также являются и 8-связными. Обратное в общем случае неверно — пикселы (О, 0) и (1, 1) являются 8-связными, но не 4-связными.

Множество пикселов на растровой сетке является связным (4- или 8-связным), если для любых двух ее пикселов существует такая последовательность пикселов, начинающаяся с первого и заканчивающаяся последним пикселом, что любые два последовательных пиксела являются соседними (т.е. 4- или 8-связными).

Соответственно, при растеризации идеальных математических объектов (которые являются связными), таких как отрезки, дуги и треугольники, мы можем требовать, чтобы получающееся при этом множество пикселов также было связным. В зависимости от выбранного типа связности мы получаем 4-связную и 8-связную растровые развертки объектов.

Одним из простейших алгоритмов растеризации является алгоритм Брезенхейма. Далее покажем, как путем ряда последовательных преобразований можно прийти к варианту алгоритма Брезенхейма, известному как метод серединной точки. При этом будем рассматривать построение 8-связной развертки отрезка.

Пусть у нас есть отрезок АВ, заданный своими концами — точками А (х_а> у_а) и B (x_h, у_ь) с целочисленными координатами. Наложим на эти координаты одно дополнительное условие:

о ^Уь~У" <^хь~Уь (рис- 7.3).

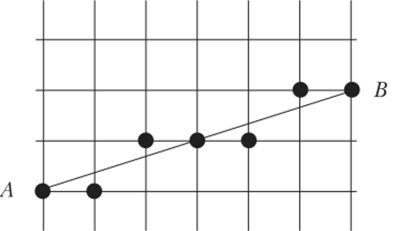
Рис. 7.3. Растеризация отрезка АВ.

Общий случай произвольного отрезка легко может быть сведен к данному путем несложных преобразований, таких как перестановка местами точек А и В, а также координат х и у.

Самый простой способ получения 8-связной развертки отрезка АВ заключается в использовании уравнения прямой, проходящей через точки Л и В в виде у = kx + b. При этом, в силу наложенного условия, 0 < k < 1. Тогда для каждого х можно найти единственное соответствующее ему значение г/, просто округлив значение kx + b до ближайшего целого числа.

Ниже приводится исходный код для этого подхода, через putPixel обозначена функция, выводящая пиксел с заданным цветом в точке с заданными координатами, и через round обозначена функция для округления значения с плавающей точкой до ближайшего целого числа:

Обратите внимание, что данный код крайне неэффективен. Мы можем несколько повысить его эффективность, отказавшись от явного вычисления выражения kx + b для каждой итерации цикла, заменив его рекуррентным соотношением:

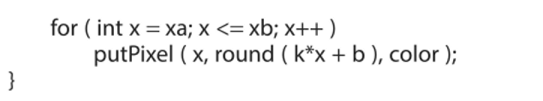
Следующей оптимизацией является отказ от использования функции round. Вместо этого мы будем явно отслеживать дробную часть выражения kx + b:

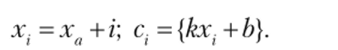
Тогда если для i-го пиксела с_{ < ½, то округляем значение вниз, иначе — округляем значение вверх. При переходе от i-й точки к (г + 1)-й положим с_м =c_j + &, если с, < ½, и с_м =c_i+k — 1 — в противном случае. Изначально х₀ = х_а, у₀ = у_а и с₀ = 0. Таким образом, приходим к следующему коду:

Еще один шаг оптимизации — вместо сравнения с_; с ½ сравнивать d. = 2с_; -1с нулем, поскольку это проще:

Заключительным шагом оптимизации будет полный отказ от использования чисел с плавающей точкой. Несложно убедиться в том, что все вещественные числа, используемые в данном алгоритме, имеют вид целого числа, умноженного на —-—. Поэтому,.

^хь-^х*

если мы умножим все dj на х_ь — х_а, то придем к использованию только целых чисел. В результате приходим к следующему коду, использующему только целые числа и операции с ними:

Описанный выше алгоритм можно легко модифицировать для получения 4-связной развертки отрезка.

Далее перейдем к задаче растеризации треугольника. Эта задача крайне важна, поскольку основная часть геометрии для рендеринга задается в виде наборов треугольников и современные GPU имеют аппаратную поддержку растеризации треугольников.

Обратите внимание, что если просто растеризовать ребра треугольника, а затем заполнить пространство между ними, то можно получить пикселы, лежащие вне исходного треугольника (рис. 7.4).

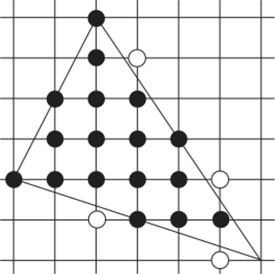
Рис. 7.4. Растеризация ребер треугольника.

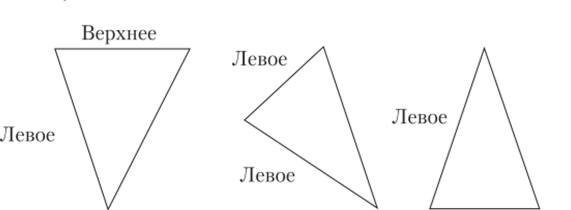
Рис. 7.5. Верхние и левые ребра для набора треугольников.

Очень часто модели задаются в виде наборов треугольников, при этом одно и то же ребро, как правило, принадлежит сразу двум треугольникам. Поэтому крайне нежелательно не только получение пикселов, не лежащих внутри треугольника, но и получение дубликатов, т. е. когда один и тот же пиксел получается при растеризации двух соседних треугольников, — каждый пиксел в этом случае должен возникать всего один раз. Во избежание этого обычно используют следующий подход: пиксел генерируется только тогда, когда его центр либо лежит строго внутри треугольника, либо когда он лежит на верхнем или левом ребре треугольника (рис. 7.5).

Дальше рассмотрим алгоритм растеризации треугольника, который часто используется в графических процессорах. Этот алгоритм очень прост и эффективен. Основная идея алгоритма заключается в том, что произвольный треугольник можно описать с помощью трех прямых, проходящих через его ребра (рис. 7.6).

Рис. 7.6. Треугольник, задаваемый с помощью трех прямых.

Произвольная прямая, задаваемая уравнением Ах + By + С = О, разбивает всю плоскость на две полуплоскости: в одной из них Ах + Ву+С >0, в другой — Ах + Ву+С <0. При этом мы всегда можем считать, что наш треугольник лежит в полуплоскости Ах + Ву+С >0. Если это не так, достаточно просто умножить уравнение прямой на -1. Тогда весь треугольник может быть представлен как пересечение трех полуплоскостей, задаваемых уравнениями А.х + В. у+С. >0, i = 1,2,3. В результате, для того чтобы проверить, лежит ли заданный пиксел внутри треугольника, достаточно просто подставить его координаты в уравнения этих плоскостей. Если при этом все три полученные числа положительны, то пиксел лежит внутри треугольника, если получено хотя бы одно отрицательное значение — то соответствующий пиксел лежит вне треугольника.

Ниже приводится код, который, но трем точкам находит коэффициенты прямой, проходящей через первые две так, что третья точка лежит в положительной полуплоскости относительно этой прямой:

Зная координаты вершин треугольника, можно найти все необходимые коэффициенты прямых. Также, но координатам вершин нетрудно рассчитать минимальный прямоугольник с ребрами, параллельными координатным осям, содержащий наш треугольник внутри. Подобный прямоугольник описывается уравнениями Т, и" *х <�х_тах, у_тт <�у<�у_тт. Далее просто перебираем все целочисленные точки, лежащие внутри этого прямоугольника, и для каждой из них проверяем, лежит ли она внутри треугольника.

Таким образом, задача растеризации состоит в определении минимального прямоугольника, содержащего треугольник, построении уравнений прямых, проходящих через ребра этого треугольника, последующего перебора всех точек сетки из прямоугольника и проверке их на принадлежность треугольнику.