Модель многоступенчатого управления

В этом подразделе будет рассмотрено явление, известное в теории управления техническими системами. В действительности оно наблюдается в весьма общей ситуации, связанной с многоступенчатым управлением самыми разнообразными системами.

Конкретизируем модель следующим образом. Пусть производство какого-то определенного продукта х управляется некоторым руководителем (или запрограммированным устройством), принимающим решение о скорости производства. Офаничимся простейшим предположением:

В свою очередь поведение руководителя, определяемое величиной у, управляется руководителем более высокого ранга, принимающим решение о том, как именно нужно менять скорость производства:

Поведение руководителя второго ранга z управляется руководителем третьего ранга и т. д., вплоть до генерального руководителя (ранга «), принимающего самостоятельные решения.

Именно такой генеральный руководитель в рассматриваемой модели реализует обратную связь, поскольку его решения основываются не на необходимости выполнить указание начальства (как у руководителей более низкого ранга), а на интересах дела. Например, он может стараться добиться определенного уровня X производимой величины х. При этом он будет влиять на своего непосредственного подчиненного — руководителя предыдущего ранга — в положительную сторону, если уровень Xеще не достигнут, и в отрицательную, если уровень Xуже превзойден.

Для структуры с тремя руководителями (п = 3) такая простейшая модель управления описывается системой уравнений.

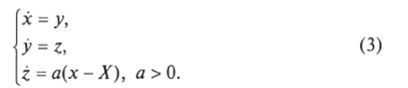
Эту систему п дифференциальных уравнений первого порядка можно записать в виде одного линейного дифференциального уравнения порядка п:

Уравнение (4) для рассматриваемой жесткой модели решается в явном виде. Устойчивость желаемого стационарного состояния х = X, у = z = = 0 определяется тем, отрицательны ли вещественные части всех корней X характеристического уравнения.

Корни этого уравнения — комплексные числа, представляющие собой все различные корни порядка п из отрицательного числа — а. Эти корни образуют на плоскости комплексной переменной X вершины правильного и-угольника:

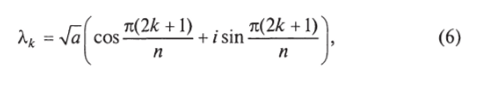
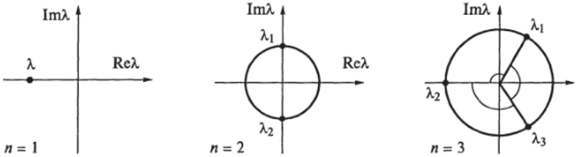
Рис. 1.29.

где к = О, 1, 2, п — 1. На рис. 1.29 показано положение корней для случаев п = 1, 2, 3. При п = 1 единственный корень = -к лежит на отрицательной части оси ReA. и решение устойчиво. При п = 2 корни Л] ₂ = ± /n/? лежат на мнимой оси ImA. и двухступенчатое управление приводит к гармоническим колебаниям (но не вызывает катастрофическое нарастание колебаний). Корни лежат на границе устойчивости.

В результате рассматриваемая жесткая модель приводит к выводу, что многоступенчатое управление при п> 3 неустойчиво. Устойчивость обеспечивает только одноступенчатое управление, при котором руководитель озабочен только интересами дела, а не указаниями других лиц. Эти выводы, сделанные на основе анализа простейшей жесткой модели, выдерживают проверку на структурную устойчивость: результаты остаются справедливыми и для близких мягких моделей, исключая случай п = 2 (двухступенчатое управление может оказаться как устойчивым, так и неустойчивым, в зависимости от деталей организации управления, которыми пренебрегают в самой простой модели).

Задачи и упражнения

• 1. Постройте решение уравнения (4).
• 2. Получите выражение (6) для корней характеристического уравнения (5).
• 3. Покажите справедливость утверждений относительно устойчивости решений, сделанных для случаев п = 1, л = 2, и л > 3 в рассмотренной жесткой модели.

Литература

: [2], [14].