Оценивание результатов моделирования

Пусть для массива выходных данных имитационной модели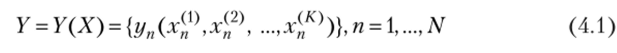

считается выполненным соотношение.

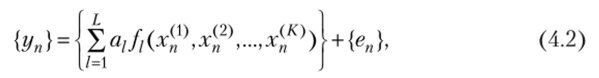
где cij — неизвестные коэффициенты; // — некоторые функции (регрессоры) входных переменных X; {е_п} — случайные отклонения.

Тогда соотношение (4.2) является наиболее общей записью линейной регрессионной модели, на основании которой в линейном регрессионном анализе производится количественный анализ массива (4.1). Уравнение (4.2) можно также представить в векторном виде:

где Y — вектор зависимой переменной размерности N; F — матрица регрессоров размерности N х Ц А — подлежащий оцениванию вектор неизвестных параметров размерности LE — вектор случайных отклонений размерности N.

В стандартной процедуре классического регрессионного анализа для оценивания неизвестного векторного параметра А обычно используется метод наименьших квадратов (МНК). Согласно этому методу минимизируется сумма квадратов отклонений:

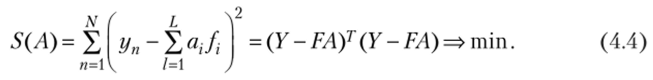
Для нахождения минимума выражение (4.4) дифференцируется по Л и приравнивается к нулю, т. е.

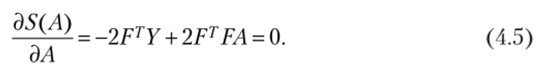
Если матрица (F^TF) ¹ не вырождена, то умножением выражения (4.5) слева на эту матрицу находится известное решение.

В этом случае имеет место теорема Гаусса — Маркова. Для того чтобы оценка (4.6) являлась несмещенной, эффективной и состоятельной, необходимо выполнение следующих условий (схема Гаусса — Маркова):

• 1) на вектор неизвестных параметров А не наложено никаких ограничений;
• 2) матрица X — не случайна (детерминирована);
• 3) вектор Е — случайный, откуда следует, что Y — также случайный вектор с распределением того же вида, что и Е;
• 4) математическое ожидание случайной величины {е_п} равно нулю;
• 5) значения случайной величины {<е_п} не коррелированы и имеют одинаковые конечные дисперсии;
• 6) случайная величина Е имеет нормальное распределение;
• 7) ранг матрицы F равен L.

Особого внимания заслуживают условия 3), 4), 5) вследствие того, что имитационная модель может не обеспечить их реализацию. Поэтому применение МНК при формировании регрессионных зависимостей, строго говоря, в ряде случаев будет заведомо необоснованным.

При невыполнении отмеченных условий целесообразно воспользоваться М-робастиыми алгоритмами оценивания. М-оценки векторного параметра Л в этом случае получаются из решения минимизационной задачи.

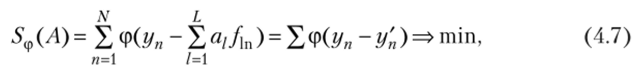
где функция ф (z) симметрична относительно оси ординат, имеет непрерывную производную и достигает минимума при 2 = 0. Если, например,.

то очевидно, что для функции (4.8) при v = 2 формула (4.7) совпадает с уравнением (4.2), т. е. оценки векторного параметра А являются МНКоценками. Для получения же робастных оценок достаточно выбрать значения v, принадлежащие открытому интервалу (0, 2). В частности, при v = 1.

(4.7) превращается в метод наименьших модулей. Таким образом, в отличие от выражения (4.3), уравнение (4.7) позволяет генерировать оцениватели различного вида.

Для того чтобы найти минимум 5_ф(Л), достаточно продифференцировать выражение (4.7) по й: и полученные выражения приравнять нулю:

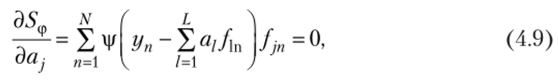
где |/(z) — производная от ф (г) по 2.

Для генерирования необходимых робастных М-оценивателей наиболее целесообразно использовать функцию |/(z), которая имеет такую же простую структурную формулу, как и функция (4.8):

Для этой функции.

Данная ф-функция удовлетворяет всем указанным выше условиям. Кроме того, она выпукла. Следовательно, для этой функции выражения.

(4.7) и (4.9) эквивалентны и имеют единственное решение. В этом случае.

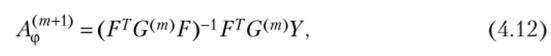
где т = 0, 1,… и для v > 1 в качестве начального приближения Л^⁰⁾ выбирается значение Л, подсчитываемое по формуле (4.6). При этом.

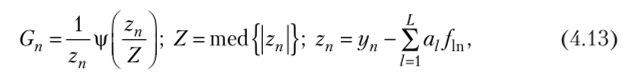
где при условии, что Zj < z₂ < … < z_N, med (z") = Z (_{AI+1) /2} для нечетных N и med (z") = (z_N/2 + z_jV/2+1)/2 для четных N.

Для случая нелинейной по параметрам модели оценивание неизвестного вектора А также используется МНК, г. с. минимизируется сумма квадратов отклонений:

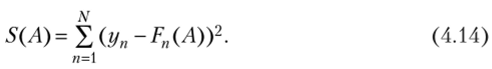
Однако, в отличие от линейных моделей, система уравнений Э$/дА = О нелинейная, поэтому вместо ее решения обычно ищется непосредственно минимум 5(Л). Для этого существует большое количество различных численных методов оптимизации:

• • методы нулевого порядка (метод покоординатного спуска Хука — Дживса, симплексный метод Нелдера — Мида и др.);
• • методы первого порядка (градиентные методы, методы Дэвидона — Флетчера — Пауэла и Флетчера — Ривса, метод Ньютона — Гаусса и др.);
• • методы второго порядка (метод Ньютона — Рафсона и др.).

В методах нулевого порядка при поиске минимума функции (4.14) используются только значения этой функции в некоторых точках; в методах первого порядка вместе со значениями функции используются ее производные, а в методах второго порядка наряду со значениями функции и ее первой производной используется также матрица, содержащая значения ее вторых производных.

Для решения задач оценивания в условиях нелинейности наиболее целесообразно использовать методы первого порядка, и в частности, метод Ньютона — Гаусса. Главная идея этого метода заключается в линейной аппроксимации функции регрессии F (A).

Пусть AN") является известным для т-го шага приближением вектора параметров А. Тогда, разложив F (A) в окрестности AN") в ряд Тейлора, с точностью до членов второго порядка получим.

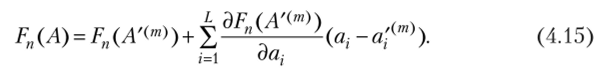
Введя обозначение Р_{1(А^Г<�•'")) = ЭГ)(AN"))/да, матричное равенство (3.15) можно переписать как.

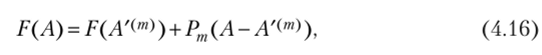
где Р_т = {Pjj (А' Р"))} — матрица производной функции F по параметрам размерности N х L.

Подставив равенство (4.16) в выражение, аналогичное (4.3), для нелинейного случая приходим к линейному, но параметрам уравнению: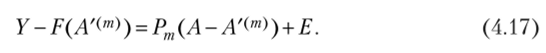

Если считать, что в схеме Гаусса — Маркова выполнены условия 1), 6) и 7), то в соответствии с выражениями (4.6) и (4.17) получим.

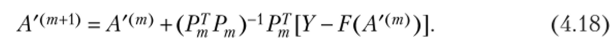
Существенным при этом является то, что для нахождения А'(^т'> необходимо использовать рассмотренный М-робастный алгоритм оценивания (с учетом того, что вместо матрицы F во все формулы следует подставлять матрицу Р_т). Однако в силу специфики решения (4.18) для обеспечения сходимости итерационных процедур в определяющие А'(^от+1> рекуррентные соотношения обычно вводят переменный коэффициент Х_тУ значение которого на каждом т-м шаге выбирается гак, чтобы выполнялось условие.

Поэтому вместо выражения (4.18) можно воспользоваться, например, формулой.

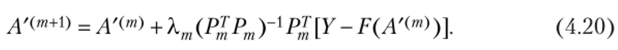
Из изложенного следует, что, взяв за основу метод Ньютона — Гаусса, можно создать большое число разнообразных алгоритмов нелинейного оценивания, каждый из которых учитывал бы специфику решаемой задачи, как для определения Л, так и для нахождения коэффициента X.