Характеристика тесноты связи

Для определения тесноты связи рассчитывается коэффициент множественной корреляции R. О R R не присваивается знак, т.к. факторы находятся в разной парной (прямой и обратной) зависимости с результативной переменной.

Для уравнений регрессии в стандартизованном масштабе при линейной зависимости R имеет вид:

Для определения степени влияния вариации факторных признаков на вариацию зависимого признака рассчитывается коэффициент множественной детерминации DR², частные коэффициенты детерминации.

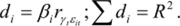
Для случаев нелинейной зависимости коэффициент множественной корреляции рассчитывается как результат сопоставления двух дисперсий: остаточной <�г*_ст и общей.

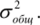
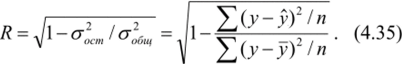
Проверка статистической надежности уравнения множественной регрессии.

В регрессионном анализе при использовании в качестве первичной информации выборочных данных результаты расчетов в значительной степени зависят от способности выборочного уравнения регрессии отображать закономерности, существующие в генеральной совокупности. Важное значение при этом имеет правильный выбор типа аналитической функции, качество подбора параметров множественного уравнения, степень разброса исходных данных относительно линии регрессии.

Для оценки статистической надежности множественных моделей могут применяться различные показатели, особое место среди них занимают /-критерий Стьюдента и^{-критерий} Фишера.

Для проверки существенности коэффициентов регрессии определяется расчетное значение /-критерия.

которое сопоставляется с табличным значением Величина t_ma5j находится с учетом числа степеней свободы к=п-р-1, где п — количество наблюдений, р — количество факторов и доверительной вероятности Р. Если то это свидетельствует о том, что корреляционная связь существует между признаками у, и х_и, х₂₁,…, х не только в выборочной, но и в генеральной совокупности.

Значимость коэффициентов чистой регрессии устанавливается следующим образом. Определяется расчетная величина /-критерия для каждого /-го коэффициента, которая сравнивается с табличной.

где Ац — диагональный элемент матрицы, обратной по отношению к матрице системы нормальных уравнений. Если / > t_ma6,, то значение /-го коэффициента пропорциональности в выборочном уравнении регрессии незначительно отличается от коэффициента регрессии, которое можно было бы построить по материалам всей совокупности. В противном случае надежность /-го коэффициента следует считать недостаточной, а соответствующий факторный признак^{рекомендуется} исключить из числа переменных в уравнении регрессии.

При необходимости по известным t_ma6ll, cг, можно рассчитать доверительную зону для выборочного коэффициента:

Для оценки надежности уравнения регрессии в целом рекомендуется использовать F-критерий Фишера.

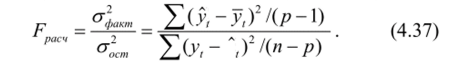
Если F_pac4 > F_ma6l для к,=р-1 и к₂=п-р и доверительной вероятности Р, то уравнение множественной регрессии следует признать статистически значимым. В противном случае гипотеза об адекватности уравнения отбрасывается.

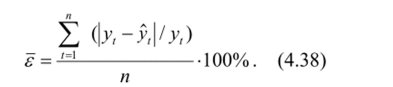
Также для обобщенной оценки уравнения множественной регрессии определяется средняя ошибка аппроксимации:

Допустимой ошибкой является ошибка, не превышающая 15%.