Системы счисления. 
Собственные имена чисел

Вопросы для обсуждения

• • В чем практическая необходимость именования натуральных чисел?
• • Каковы связи между нумерацией чисел и действиями над ними?
• • Каковы преимущества позиционных систем счисления перед непозиционными системами?
• • Почему знакомство детей с различными системами счисления способствует освобождению «от власти знака»?
• • Каковы принципы позиционной системы счисления?
• • Что такое разрядная единица? Как связаны понятия «разрядная единица» и «основание системы счисления»?
• • Каковы связи между счетом группами и мультипликативным принципом построения позиционной системы счисления?
• • Почему позиционная система счисления по основанию десять стала общепринятой?
• • В чем преимущество двоичной, восьмеричной и шестнадцатеричной систем счисления для компьютера?
• • Что дает ознакомление младших школьников с системами счисления по разным основаниям, принятое в учебнике по системе Б. Д. Элькопина — В. В. Давыдова?

Практическое применение натуральных чисел невозможно без присвоения каждому из них собственного имени. Исторически именования чисел возникали и развивались вместе с увеличением количества используемых в практике предметов, требующих их пересчета, и вместе с тем с уточнением и расширением представлений об арифметических действиях. Общепринятая в настоящее время десятичная позиционная система возникла по историческим меркам сравнительно недавно, около VII в. в Индии. Даже греки не смогли построить такой системы, одной из причин, может быть самой существенной, было отсутствие нуля. В самом деле, введение нуля нельзя расценивать иначе как интеллектуальный прорыв: «ничего» стало чем-то! Греки мыслили число как совокупность единиц, что исключало появление нуля. Так как наша культура, в том числе и математическая, имеет истоки в Древней Греции, то, возможно, поэтому вопрос о том, является ли нуль натуральным числом, в практике обучения до сих пор является дискуссионным.

Сам принцип позиционности, основываемый на переходе к счету укрупненными единицами, был известен и повсеместно использовался еще за 2 тыс. лет до н.э. вавилонянами. Каждый раз, когда для пересчета некоторой совокупности предметов хорошо известного отрезка натурального ряда не хватало, счетная единица укрупнялась. Если ее укрупнение происходило всегда в одно и то же число раз, то получаемые единицы становились единицами соответствующего разряда. Место записи таких единиц однозначно определялось разрядом. Число, которое показывает, во сколько раз увеличивается разрядная единица, называется основанием системы счисления. Оно может быть любым натуральным, большим единицы. Если а — мощность конечного множества, то процедура присвоения ему собственного имени, но основанию р = 3 демонстрируется описанием на языке знаков-индексов на рис. 3.14.

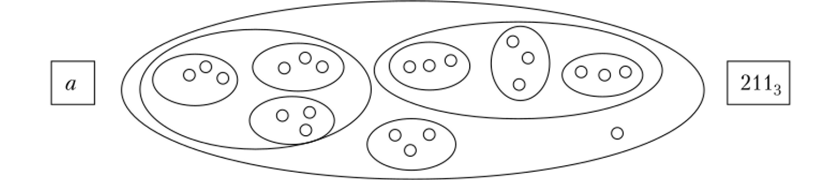
Рис. 3.14. Процедура присвоения численности множества собственного имени Предполагая, что безошибочно считать мы можем только до трех, а пересчитываемых предметов больше трех, мы на каждом шаге укрупняем счетную единицу в три раза. Пересчитываемых предметов более трех, начинаем считать тройками, полученных троек также более трех, начинаем считать тройками троек, их две. Прибегая к укрупнению счетной единицы в первый раз, мы находим число единиц второго разряда, содержащихся в числе а. от счета единичными предметами переходим к счету тройками предметов. В результате получаем две тройки троек, одну тройку, одну исходную единицу. Таким образом, число а содержит две единицы третьего разряда, каждая единица которого состоит из тройки троек, одну единицу второго разряда, состоящего из трех единиц первого, и одну единицу первого разряда. Договорившись, что разряды начиная с самого крупного записываются слева направо, в итоге получаем: а — 211₃, где 3 — основание системы счисления.

Пример. Построим рассуждение, ведущее к поиску ответов на вопрос: сколько единиц, десятков, сотен, десятков сотен, тысяч содержится в числе 121 132. Используем таблицу разрядов.

Таким образом, в данном числе:

• 100 000 + 20 000 + 1000 + 100 + 30 + 2 = 121 132 единицы;
• 10 000 + 2000 + 100 + 10 + 3 = 12 113 десятков;
• 1000 + 200 + 10 + 1 = 1 211 сотен;
• 100 + 20 + 1 = 121 тысяча;
• 10 + 2 = 12 десятков тысяч;
• 1 сотня тысяч.

Возникает вопрос, всегда ли возможна такая процедура и является ли эта запись при выбранном основании единственной? Если возвратиться к рис. 3.14, то легко заметить, что представленная процедура состоит из следующей последовательности шагов: на первом шаге это операция деления с остатком числа а на 3, затем деления с остатком на 3 полученного на первом шаге частного, далее деления с остатком на 3 полученного на предыдущем шаге частного, которое равно 0. Последовательность остатков начиная с последнего есть запись числа а по основанию 3.

Обоснование указанной процедуры дается следующими теоремами.

Теорема 1. Если а и b — любые два натуральных числа и b Ф 0, то можно найти такие натуральные q и г, что выполняется равенство.

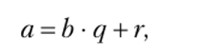
при этом 0 < г < Ь_у г и q определяются однозначно.

Доказательство. Предположим сначала, что а > Ь. Рассмотрим числа, кратные b: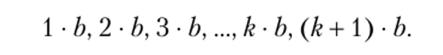

В силу аксиомы Архимеда найдется натуральное q такое, что b • q < а, тогда как b • (q + 1) > а. Обозначим а — b q = r, очевидно, г > 0. Отсюда а = = b? q + г, но b • (q + 1) = b • q + b > а, т. е. b-q + b>b-q + r, следовательно, г < Ь. Для этого случая существование q и г доказано.

Если а— Ъу то q — 1, г — 0. Если b > а_у то q = 0, г = а.

Докажем теперь, что q и г определяются однозначно. Допустим, что а = = b — q + г = b — q_x + r_v где 0 < г < b и 0 < г_{ < Ь. Тогда b • q — b • q_x = i — г, или b-(q-q₁) = r_l— г. Здесь правая часть меньше b_f тогда как левая часть делится на b, следовательно, г_х — г = 0, ? = г, q_x— q. Теорема полностью доказана.

Теорема 2. Любое натуральное число а единственным образом представляется в виде.

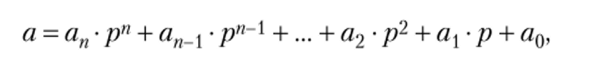
где cij — имена чисел, не превышающих основание системы счисления р. Такие числа обозначаются знаком — цифрой. Цифры образуют алфавит системы счисления. Так, в десятичной системе цифрами являются 0, 1,…, 9. Вообще в позиционной системе счисления, но основанию р цифрами обозначаются числа от 0 до р — 1, т. е. цифр ровно р. В примере на рис. 3.14 р = 3, а алфавит троичной системы счисления А = {0, 1, 2}.

Доказательство. Так как представление числа в позиционной системе счисления есть последовательное деление с остатком на основание системы счисления, то процесс такого деления заканчивается в силу того, что последовательность неполных частных убывает. Результат является единствененным в силу однозначности деления с остатком.

Позиционная система счисления представляет имена чисел как последовательности «слов» в алфавите А = {0, 1,1}, причем последовательности.

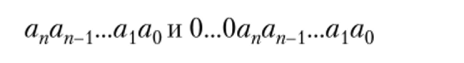
считаются совпадающими. Числа, записываемые только «буквами» алфавита, называются однозначными, остапьные — двузначными, трехзначными,…, многозначными.

Процедура именования числа по выбранному основанию позволяет осуществлять «перевод» числа, записанного по основанию р, в запись этого числа по другому основанию. Особенно просто осуществляется такой перевод в десятичную систему счисления, в силу того что таблицы сложения и умножения в ней нам хорошо известны. Например:

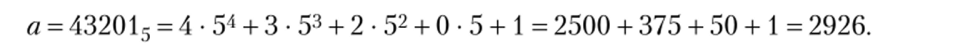
Так же просто можно осуществить «обратный» перевод числа 2926 в пятеричную систему счисления. Для этого надо воспользоваться процедурой деления с остатком. Получаем следующую систему равенств:

Итак, 2926 = 43 201₅.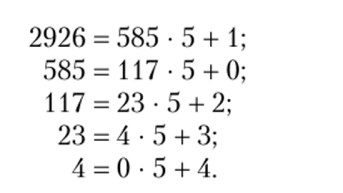

жения и умножения по основанию р

Несколько сложнее обстоит дело в том случае, если требуется перевести 43 201₅ в запись числа по основанию, например, 3. Построим таблицы сложения и умножения по основанию р = 5.

Таблица сложения по основанию Р = 5.

Таблица умножения, но основанию Р = ⁵

Делим последовательно на 3 число 43 201₅ до тех пор, пока не получим частное, равное нулю. Все действия производим в пятеричной системе по известному алгоритму деления углом. Получаем следующие равенства:

Отсюда 43 201₅ = 11 000 101₃.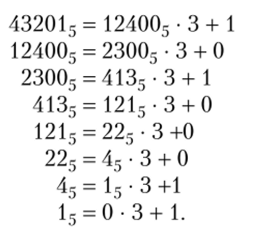

Обратный перевод (все действия производим по известным алгоритмам умножения и сложения в столбик в пятеричной системе; показатели степеней даны в десятичной системе):

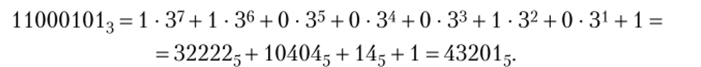
Позиционная система счисления открывает возможность производить действия с числами независимо от природы числа, оперируя только соответствующими символами, но определенным алгоритмам, использование которых значительно упрощается предварительным составлением и запоминанием таблиц сложения и умножения однозначных чисел.

Таблица сложения, но основанию Таблица умножения по основанию р=3 р=3.

Значения сумм и произведений могут быть найдены применением определений соответствующих действий. Например, если рассматривать 0, 1 и 2 как имена мощностей конечных множеств, то сумма и произведение 2 + 2 и 2 • 10 находятся так, как показано на рис. 3.15, где выделенное множество образует единицу второго разряда, обозначаемую 10.

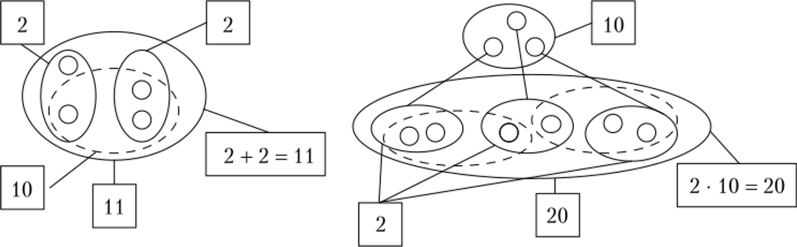
Рис. 3.15. Нахождение суммы 2 + 2 и произведения 2 • 10 в троичной системе счисления Числа, записанные в позиционной системе счисления:

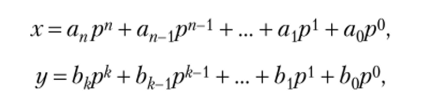
можно складывать поразрядно, начиная с разряда единиц. Складываемые в каждом разряде числа меньше основания системы счисления, однозначные, а их суммы меньше самого большого числа в таблице сложения. Так как самые большие слагаемые в таблице сложения равны р — 1, то сумма в каждом разряде не превышает числа.

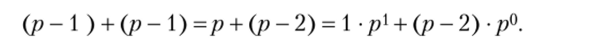
Например, при р = 3 это число 11₃, при р = 5 это число 13₅.

Значит, в каждом разряде сумма представляет собой не более чем двузначное число, в котором единиц второго разряда одна, и р — 2 — наибольшее возможное число единиц первого разряда. Так как двузначное число нельзя записать в соответствующем разряде суммы, то в этом разряде записывается число единиц того же разряда, а единица следующего разряда прибавляется к сумме единиц следующего разряда. Теоретическая основа этого алгоритма — ассоциативность, коммутативность сложения, дистрибутивность умножения относительно сложения.

Произведение р-ичного числа на однозначное число а равно.

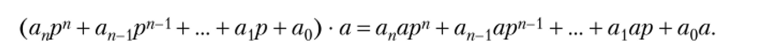
Так как 0 < а_х <�р — 1, г — 0, 1, …, /г, и а <�р — 1, то любое произведение а_х • а находится в соответствующей таблице умножения и не превышает произведения.

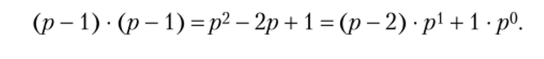
Это запись двузначного числа по основанию р, в первом разряде которого 1, а во втором р — 2. При р = 3 это число 11₃, при р = 5 это 31₅, при р = 7 это 51₇. Поэтому, умножая число единиц любого разряда на а, получим либо однозначное число, которое записывается в соответствующем разряде произведения, либо двузначное число, число единиц которого записывается в соответствующем разряде, а число единиц второго разряда прибавляются к произведению в следующем разряде. Теоретической основой этого алгоритма является дистрибутивность умножения относительно сложения, коммутативность и ассоциативность сложения и умножения.

Произведение а = а_пр^п + а_п__хр^п-^{ + … + а_лр + а₀ на многозначное число находится как сумма произведений на разрядные слагаемые. Если записать число а непосредственно в системе по основанию р, то получим.

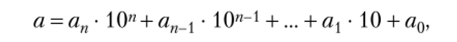
где dj — цифры р-ичной системы счисления, а 10 — обозначение числа, равного р, в р-ичной системе.

Отсюда.

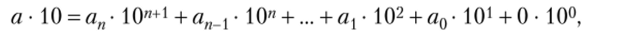
т.е. в этом произведении увеличилось на один число разрядов, а число единиц в нервом разряде стало равным нулю. Другими словами, запись результата умножения а на 10 отличается от записи а приписыванием к а нуля справа. Если же умножать на степень 10, то приписывать надо столько нулей, какова степень множителя.

Тогда запись результата деления числа, оканчивающегося нулями на степень 10 (если их не меньше, чем степень 10), отличается от записи делимого удалением справа стольких нулей, какова степень делителя. Действительно, если а • 10″ = «00…0, где п нулей, то.

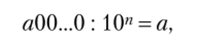
так как частное — это такое число, умножая которое на делитель, получаем делимое.

Алгоритм деления р-ичных чисел основан на последовательном вычитании делителя из делимого, начиная с высших разрядов. Его теоретической основой служит деление с остатком. Каждый знак в представлении числа по основанию р показывает число соответствующих единиц в данном разряде. Всех соответствующих разрядных единиц в числе столько, сколько их обозначено числом, образованным всеми цифрами, стоящими перед этим разрядом и цифрой данного разряда. Например, в числе 201 809 всего 201 809 единиц, 20 180 десятков, 2018 сотен, 201 тысяча, 20 десятков тысяч и 2 сотни тысяч. В разряде единиц этого числа — 9 единиц, в разряде десятков — 0 единиц, в разряде сотен — 8 единиц, в разряде тысяч — 1 единица, в разряде десятков тысяч — 0 единиц, в разряде сотен тысяч — 2 единицы.

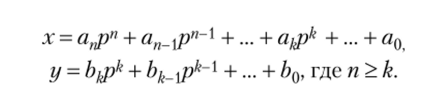
Пусть Если.

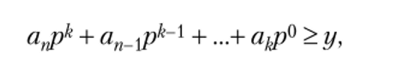
то частное х/у получается последовательным вычитанием чисел соответствующих разрядов, кратных г/, пока в остатке нс получится нуль, если у кратно х.

Например, процедура нахождения частного 19 872/736, где 198 < 736, представляется следующим образом:

Принято эту процедуру записывать «углом».

В вычислительной практике арифметические действия на протяжении веков производились с использованием некоторых инструментальных средств. Чаще всего это были различные виды абаков. Например, абаком являются русские счеты. Судя по некоторым дошедшим до нас описаниям, абак можно представлять также в виде доски, разграфленной на полосы, в которых помещались предметы (камешки, фишки, жетоны), обозначавшие количество единиц в соответствующем разряде. Эти предметы можно было передвигать из одного разряда в другой, в зависимости от получаемых в процессе вычислений результатов. По-видимому, именно абак оказал решающее влияние на становление позиционной системы счисления. То, что эта система оказалась десятичной, объясняется исключительно наличием у человека десяти пальцев на руках, которые также служили естественным счетным инструментом. Сегодня электронные вычислительные инструменты стали повседневной реальностью, но это не значит, что техника устных и письменных вычислений не должна изучаться в школе, хотя акцент должен смещаться в сторону выявления процесса построения соответствующего алгоритма.

В связи с тем что курс математики начальной школы интегрируется с курсом информатики, особое значение приобретает ознакомление детей с позиционными системами по различным основаниям и алгоритмам перевода чисел из одной системы счисления в другую. Думается, что простое запоминание соответствующих алгоритмов вряд ли целесообразно в начальном математическом образовании. Известно, что в современной вычислительной технике, в устройствах автоматики и связи используется в основном двоичная система счисления. Ее недостаток — быстрый рост числа разрядов, необходимых для записи даже небольших чисел. Поэтому если возникает необходимость кодировать информацию «вручную», то используют восьмеричную или шестнадцатеричную системы счисления: числа 8 и 16 — соответственно 3-я и 4-я степени числа 2. Поэтому перевод двоичных чисел в восьмеричную и шестнадцатеричную системы и обратно осуществляется просто. Для шестнадцатеричной системы десятичных цифр недостаточно, с этой целью используются буквы А, В, С, D, Е, F, которые обозначают соответственно числа 10, 11, 12, 13, 14, 15.

Чтобы перевести число из двоичной системы в восьмеричную, надо разбить его на триады справа налево и заменить каждую триаду соответствующим восьмеричным числом. Например, 1 010 111 112 = 537₈, так как 101₂ = 5₈, 11₂ = 3₈, 1112 = 7₈. Действительно,.

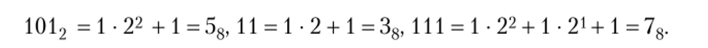
Обратное действие аналогично: каждую цифру восьмеричного числа заменяем двоичным числом, имеем:

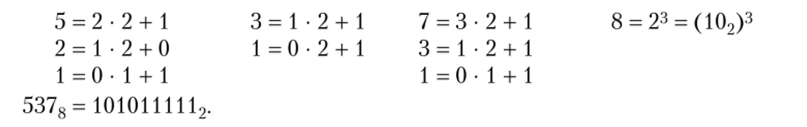
Аналогично осуществляется перевод шестнадцатеричных чисел в двоичные и обратно. Двоичное число разбивается на тетрады, а каждая тетрада заменяется соответствующим шестнадцатеричным числом. Самое большое трехзначное число в двоичной системе — 111₂ = 7₈, а самое большое четырехзначное число в шестнадцатеричной — 1111₂ = F₁₆. Это самые большие однозначные числа в соответствующих системах счисления.

Задания для самостоятельной работы.

1. Число а задано конкретным представителем класса равномощных множеств — множеством, приведенным на рисунке.

Требуется найти его запись в троичной системе счисления. Оформите решение этой задачи в форме программы действий (алгоритма).

• 2. Опишите методику работы над заданием: «Найти числа, следующие сразу за данными: 11, 22, 44, 99, если числа записаны в двоичной, троичной, пятеричной и десятичной системах счисления соответственно».
• 3. Постройте рассуждение, ведущее к поиску ответа на вопрос, сколько в числе 260 124 единиц в разряде единиц, в разряде десятков, в разряде сотен, в разряде тысяч, в разряде десятков тысяч, в разряде сотен тысяч. Найдите наглядные средства, показывающие единицу каждого разряда.
• 4. Составьте систему заданий, направленную на формирование умений записывать цифрами число по соответствующему числительному.
• 5. Составьте систему заданий, направленную на формирование умений читать число, заданное его цифровой записью.
• 6. Опишите методику работы над задачей: «Запишите числа, предшествующие
• 10,100,1000,10 000, 100 000,1 000 000».
• 7. Определите цель упражнений:
  • а) увеличьте число 102 в 10, в 100 раз;
  • б) уменьшите число 10 200 в 10, в 100 раз.

Постройте рассуждение, приводящее детей к требуемому умозаключению.

• 8. Составьте задания на классификацию чисел при изучении нумерации.
• 9. Составьте рассказы для детей: а) как люди научились считать; б) как велик миллион.
• 10. Спроектируйте фрагмент урока, обучающий детей сравнивать многозначные числа. Продумайте, какие средства обучения здесь целесообразно использовать.