Алгебраическая структура множества натуральных чисел

Множество натуральных чисел N является алгебраической структурой с операциями сложение и умножение, выделенными элементами 0 и 1 и отношением порядка, подчиняющимися следующим законам.

1. Для любых a, b е N, взятых в определенном порядке, существует единственное с е N такое, что а + b = с и существует единственное d е N такое, что ab-d (это утверждение означает, что сложение и вычитание — бинарные алгебраические операции на N).

2. Сложение и умножение имеют нейтральные элементы: для любого а е N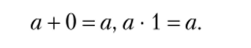

3. Сложение и умножение коммутативны: для любых a, b е N

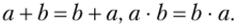
4. Сложение и умножение ассоциативны: для любых a, b, с е N

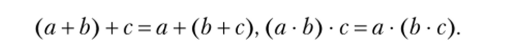
5. Умножение дистрибутивно относительно сложения справа и слева: для любых а, Ь, с е N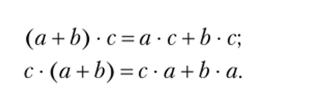

6. Сложение и умножение — сократимые операции: для любых a, b, ce N

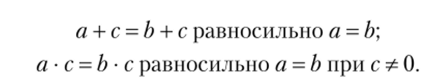
7. Нуль — поглощающий элемент умножения: для всякого а е N

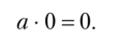
8. На N определено отношение «>»: для любых а и b е N а> b (Ь < а) тогда и только тогда, когда существует с е N, с Ф 0, такое что а = b + с.

Отношение «>» является отношением порядка, оно обладает следующими свойствами:

• • антирефлексивность (для всякого а е N а> а неверно);
• • антисимметричность (если а > Ь, то b > а неверно);
• • транзитивность (если а > b и b > с, то а > с);
• • связность (для всяких a, b е N если а * Ь, то либо а > b, либо b > а).

Доказательство. Антирефлексивность. Допустим, что а > а, тогда существует с * 0, что а = а + с, или а + 0 = а + с, отсюда 0 = с вопреки его выбору.

Антисимметричность. Допустим, что одновременно имеют место оба неравенства: а > b и b > а. Тогда существуют такие с * 0 и d Ф 0, что выполняются равенства.

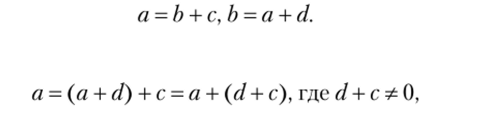
Отсюда что невозможно.

Транзитивность. Пусть а > b, b > с. Тогда а = b + и, b = с + v, и ^ 0, v Ф 0. Отсюда.

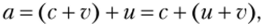
следовательно, а > с.

Связность. Пусть при афЬ имеет место а не больше b и Ъ не больше а. Возможны следующие варианты: 1) а < Ъ и а — Ь 2) а < b и b < а] 3) b < а и b = а.

В случаях 1) и 3) имеем h = Ь + с, с * 0; в случае 2) а = а + (с+ rf) при с ^ 0 и d Ф 0, что невозможно.

Таким образом, данное отношение есть отношение линейного порядка. Справедливы следующие утверждения.

• 1. Для любого a g N, а ^ 0, имеет место а > 0, так как а = () + а.
• 2. Сложение и умножение в N монотонны относительно отношения порядка. Для всяких а, Ь, с е N а > b равносильно а + с>Ь + сиа-с>Ь-с при с Ф 0.

Действительно, а > b равносильно по определению а = b + d, d * 0. Отсюда в силу единственности сложения, свойств ассоциативности и коммутативности имеем.

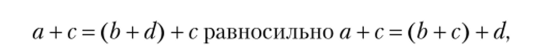
т.е. а > b равносильно а + с> b + с.

Если а = Ъ + d, с Ф 0, d Ф 0, то d • с Ф 0, отсюда.

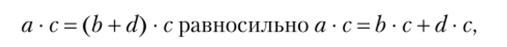
т.е. а > b равносильно а • с> b • с.

3. Для любых а, b е N таких, что а > b, уравнения.

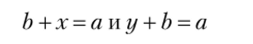
имеют единственные и равные между собой решения.

Действительно, пусть а > Ь. Тогда существует с Ф 0, что.

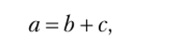
а уравнение Ь + х = а преобразуется в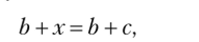

отсюда (сократимость сложения) х = с. Так как b +х = у + Ь, или b +х = b л-у (коммутативность сложения), то имеем.

Таким образом, при а > Ъ существует единственное число с, определяемое парой чисел а, Ъ. Это число с-a-b называется разностью а и Ь, а само действие — вычитанием. Если а = Ь> то решением уравнений а + х = а и у + а = а является х = у = 0, т. е. разность а — а = 0. Так как разность а — b определена не для всех пар натуральных чисел, то вычитание на N называют частичной операцией, производной от операции сложения.

Так как а — b есть решение уравнения b+x = a_t то имеет место равенство.

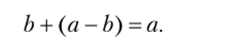
Это значит, что а-b — это такое число, которое при сложении с b дает а. Например, разность 7 — 5 — это такое число, сумма которого с числом 5 равна 7. Это число 2, потому что 5 + 2 = 7.

4. Для любых a, be N таких, что b*0na = k-b, уравнения.

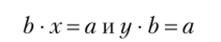
имеют единственные и равные между собой решения.

Пусть а = k • b. Тогда b • х = k • b и у • b = k • b. Отсюда в силу коммутативности и сократимости умножения получаем х = у = к. В условиях теоремы это число однозначно определяется числами а и b и обозначается а/b. Оно называется частным от деления а па Ь> а соответствующее действие — действием деления.

Частное определено не для всех пар натуральных чисел. Поэтому говорят, что деление — частичная операция на N> производная от операции умножения. Если а/b есть решение уравнения b х = а, то имеет место равенство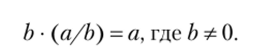

Отсюда следует, что частное а/b — это такое число, умножая которое на получаем а.

Свойства вычитания. При условии что все рассматриваемые разности существуют, для любых а, b, с е N имеют место следующие равенства:

• 1) а — 0 = а (правило вычитания 0);
• 2) а + (Ь — с) = (а + Ь) — с (правило прибавления разности к числу);
• 3) а — (Ь — с) = (а — Ь) + с (правило вычитания разности из числа);
• 4) а — (Ь + с) = (а — Ь) — с (правило вычитания суммы из числа);
• 5) а • (Ь — с) = а • h — а • с (правило умножения числа на разность);
• 6) {а + Ь) — с = а + (Ь — с) (правило вычитания числа из суммы);
• 7) а-а = 0.

Например, докажем равенство 2.

Положим bс = х, тогда Ь = с + х. Положим (а + Ь) — с = у, тогда а + b = = с + у, или а + (с + х) = с + у. Отсюда с + {а + х) = с + у. Сокращая на с, имеем а + х = у. Это и есть доказываемое равенство в новых обозначениях.

Остальные свойства доказываются аналогично. Вообще, любое доказательство свойства вычитания основывается на исключении вычитания согласно его определению и из следствий, обусловленных свойствами сложения.

Свойства деления. При условии что все рассматриваемые частные существуют, для любых а> Ь, с е N имеют место следующие равенства:

• 1) а/- а (правило деления на 1);
• 2) а • (b/с) = (а • Ь)/с (правило умножения числа на частное);
• 3) а/(Ь/с) = (а/b) • с (правило деления числа на частное);
• 4) (а + Ь)/с = (а/b) + (b/с) (правило деления суммы на число, или правая дистрибутивность деления относительно сложения);
• 5) (а — b)/c = (а/с) — (b/c) (правило деления разности на число, или правая дистрибутивность деления относительно вычитания);
• 6) а/а = 1 (правило деления числа на себя).

Докажем равенство 2. Положим b/с = х и (а • Ь)/с = у. Тогда b = с • х, а b = с • у. Подставляя в последнее равенство вместо b его значение, получим а (с • х) = с у, или, сократив на с, имеем а • х = у. В принятых обозначениях это доказываемое равенство. Остальные свойства доказываются аналогично посредством исключения деления в соответствии с его определением.

Таким образом, алгебраическая структура натуральных чисел, которая называется полукольцом с единицей, завершает рассмотрение практически важных и генетически различных теоретических моделей натуральных чисел. Алгебраическая модель синтезирует правила оперирования числами как элементами некоторой знаковой системы, которые одинаковы при любом толковании их природы.

Нелишне заметить, что свойства операций в этой алгебраической структуре нами не доказывались, а постулировались, т. е. мы полагали их таковыми. С точки зрения формальной логики нет оснований считать, что существует система объектов с такими свойствами. Разумеется, имеющиеся у нас представления о натуральных числах, сложившиеся из опыта их использования с целью решения тех или иных практических задач, позволяет нам предполагать, что эти представления по крайней мере не противоречат тем утверждениям, которые представлены в данной модели. Но можно заметить, что конструктивные числа Гильберта, или мощности конечных множеств, или меры величин удовлетворяют всем постулируемым в рассмотренной структуре свойствам сложения и умножения. В то же время и конструктивные числа Гильберта, и конечные мощности, и меры величин образуют ту наблюдаемую, хотя и идеальную, реальность, абстрагирование свойств которой приводит к алгебраической структуре, являющейся результатом более высокого уровня абстракции.

Задания для самостоятельной работы

• 1. Па основе анализа учебников математики для 1-го класса УМК «Школа России», «Перспектива», «Школа 2100», «Начальная школа XXI века»^[1] установите:
  • а) какие практические и теоретические предпосылки лежат в основе ознакомления детей с коммутативным свойством сложения;
  • б) на какие знания опирается такое ознакомление;
  • в) как в дальнейшем обучении данное свойство используется.
• 2. Приведите методические обоснования того факта, что свойства арифметических действий в учебнике М. И. Моро с соавторами чаще всего представлены в форме правил.
• 3. Выпишите все свойства арифметических действий, которые рассматриваются в учебниках М. И. Моро с соавторами и В. В. Давыдова с соавторами. Заполните таблицу.

• 4. Проведите рассуждение, которое доказывает, что определение умножения, данное в учебнике УМ1< «Школа России», неприменимо для умножения на 0 и 1. Спроектируйте фрагмент урока ознакомления детей с этими случаями умножения. Укажите теоретические основания разработанного вами подхода.
• 5. На основе анализа учебника математики УМК «Перспектива» выясните, как устные вычислительные приемы сложения и вычитания основываются на свойствах этих операций. Заполните таблицу.

• 6. Объясните, почему у вычитания и деления нет обратной операции.
• 7. Опишите наглядные средства, которые целесообразно использовать для разъяснения свойства коммутативности умножения.
• 8. Объясните, почему дистрибутивность умножения относительно сложения и вычитания можно рассматривать, как правило вынесения общего множителя за скобку.
• 9. Покажите, как можно продемонстрировать детям аналогию между свойствами ассоциативности и коммутативности сложения (умножения).
• 10. Покажите, какие аналогичные действия могут выполнить дети при нахождении разностей и частных.

• [1] Система учебников «Начальная школа XXI века» состоит ив завершенных предметныхлиний учебников, которые включены в федеральный перечень учебников, рекомендуемыхк использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования (приказМинобрнауки России от 31 марта 2014 г. № 253).