Базис гильбертова пространства

В «-мерном векторном пространстве базисом является любая совокупность п линейно независимых элементов. Каждый вектор может быть однозначно представлен в виде линейной комбинации базисных векторов. Аналогично, в случае бесконечномерного пространства V, будем называть базисом последовательность линейно независимых векторов {е,.}*!, V может быть однозначно представлен в виде сходящегося ряда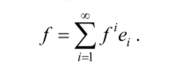

И2.

Из требования однозначности такого представления следует, что компоненты разложения /' нулевого вектора равны нулю.

Простым примером бесконечномерных пространств может служить аналог пространства R"  — пространство t, элементами которого являются бесконечные последовательности чисел х-(х', х²,…, х" ,…). Если это пространство снабдить, например, евклидовой нормой (г. е. рассматривать банахово пространство ?₂), то элементы е, =(1,0,0,…),.

е₂ = (0,1,0,…) образуют базис. Любой вектор xg(₂ может быть одно;

значно записан в виде ряда У]х'е_/, сходящегося к х по норме:

/=1.

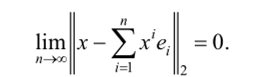
С пространством i₂ все относительно просто, так как каждый вектор х е i₂ характеризуется счетным набором чисел. В общем случае полезным оказывается понятие сепарабельности. Для того чтобы разобраться в этом, начнем с примера. Рассмотрим множество действительных чисел или пространство R^]. В нем можно выделить подмножество целых чисел Z и подмножество рациональных чисел Q. Вес остальные числа являются иррациональными. Пусть требуется вычислить приближенное значение а некоторого числа а е /?'. Приближение будем считать хорошим, если ошибка (модуль разности) не превосходит некоторой наперед заданной величины е. Если е > —, то, очевидно, а можно аппроксимировать числами и из Z, и из Q. Однако если ? может быть произвольно малым, то множеством Z, вероятнее всего, не обойтись, а множество Q по-прежнему подходит. Дело в том, что целые числа расположены на числовой оси слишком редко, или, как говорят, множество Z неплотно в /?'. Существует ли и для Q такое ?, для которого рациональные числа перестают аппроксимировать произвольное вещественное число? Оказывается, не существует. Между любыми, сколь угодно близко расположенными рациональными числами, всегда найдется еще одно рациональное число. Мы можем сконструировать такую последовательность рациональных чисел, что она будет стремиться к любому вещественному числу (не только рациональному, но и иррациональному). Таким образом, множество Q отличается от R^] только тем, что не содержит все свои предельные точки. Иными словами, /?' есть замыкание О. В этом случае говорят, что множество Q плотно в множестве Л¹. Формальное определение плотного множества таково. Пусть S_x с: S₂ с: В, В — банахово пространство. Множество S_x

называется плотным в S₂, если замыкание S_x в S₂ совпадает с S₂. Наличие в несчетном множестве /?' плотного в нем счетного множества Q позволяет сколь угодно точно аппроксимировать любое число из У?¹, пользуясь только числами из Q. Банахово пространство 5, содержащее счетное плотное множество, называется сепарабельным. Иными словами, если В сепарабельно, то существует множество S В, S = {/"}*₌₁, такое, что для любого f е В и заданного? > 0 найдется f_neS, удовлетворяющее неравенству ||/-/‘J|.

• 1. Обобщая случай У?¹, в котором множество рациональных чисел О плотно, рассмотрим векторное пространство R". Оно также содержит счетное плотное множество. Им, очевидно, будет множество элементов с рациональными координатами.
• 2. Пространство С°([а₉Ь]) непрерывных функций, определенных на отрезке [а, Ь] с равномерной нормой, также сепарабельно, так как множество многочленов с рациональными коэффициентами плотно в нем.

Если В несчетно, но сепарабельно, т. е. содержит в себе плотное подмножество 5, то любой элемент из В может быть сколь угодно точно аппроксимирован элементом счетного множества S. Это свойство позволяет в ряде случаев выбрать и в бесконечномерных пространствах удобный базис. Как уже говорилось, последовательность векторов {е,}*, из векторного пространства V образует базис этого пространства, если любой элемент / е V можно единственным образом представить в виде сходящегося по норме ряда.

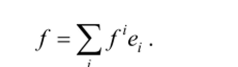
С другой стороны, если задана последовательность ненулевых линейно независимых векторов {g,.}, gjGV, то все возможные конечные (состоящие из конечного числа членов) линейные комбинации этих векторов образуют векторное пространство 5сГ. Если S = V, то элементы {g,} образуют базис V. Возникает два вопроса: 1) в каком случае S = V и 2) как выбрать элементы так, чтобы они были линейно независимы? Для того чтобы равенство S = V выполнялось, последовательность векторов {g_y} должна быть полна. Обратите внимание на то, что здесь речь идет о полноте системы векторов, а не о полноте векторного пространства. Вместе с тем понятие полноты и в том и в другом случае, по сути, означает, что элементов, будь то пространства, или последовательности векторов, или еще чего-нибудь, должно быть достаточно для того, чтобы некоторое свойство выполнялось. В случае векторного пространства элементов должно быть столько, чтобы предел любой последовательности элементов также был элементом из этого пространства, а в нашем случае последовательность должна содержать столько элементов, чтобы S = V. Более подробно мы рассмотрим свойство полноты чуть ниже, применительно к гильбертовым пространствам. Если {§ i}?= порождает пространство S, такое, что S = V, то V имеет счетную размерность, т. е. является пространством типа I, элементами которого служат бесконечные наборы чисел. Если же размерность V несчетна, то S ^ V и в лучшем случае S может быть плотно в V. Тогда любой вектор / е V можно записать в виде бесконечного ряда:

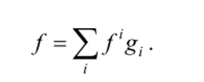
Ответ на второй вопрос связан со свойством минимальности последовательности. Понятно, что если {g,.} полна, то добавление новых элементов не лишает ее этого свойства. Векторы при этом становятся линейно зависимыми и потому не могут служить базисом. Минимальный же набор векторов {g/}, сохраняющий свойство полноты, как раз и будет линейно независимым и тем самым является кандидатом в базисы пространства V.

Свойства минимальности и полноты наиболее просто устанавливаются для ортогональных векторов. Выше мы уже доказали, что ортогональные векторы линейно независимы, следовательно, полная ортогональная система будет и минимальна. В терминах ортогональных векторов полнота определяется так. Пусть Я - гильбертово пространство и е_{ е Я . Последовательность называется полной, если ортогональное дополнение к ней равно нулю (есть множество, содержащее единственный элемент нуль). Иначе говоря, если {е,.} - полная система векторов, то не существует отличных от нуля векторов из Я, ей ортогональных, так как из (/,?.) = О для всех e.G{e_f} следует / = 0. Пусть.

Н = R³. Выберем некоторый вектор е_х е Я. Он, очевидно, не образует полной системы векторов. Подпространство, им порождаемое, есть R¹ ^ Я, а ортогональное дополнение отлично от нуля и представляет собой плоскость, проходящую через нуль перпендикулярно е_х (рис. 35, а). Выберем в этой плоскости, т. е. в ортогональном дополнении, элемент е₂ и образуем последовательность {e_t, e₂}. Она также не полна и порождает пространство Я², т. е. плоскость, а ортогональное дополнение к ней вновь не нуль, а представляет собой прямую, перпендикулярную этой плоскости (рис. 35, б). И наконец, когда мы выберем на этой прямой третий вектор е₃, то последовательность {е_х, е₂, е_г} станет полной, будет порождать пространство /?³=Я, а ортогональное дополнение к ней станет нулевым (рис. 35, в).

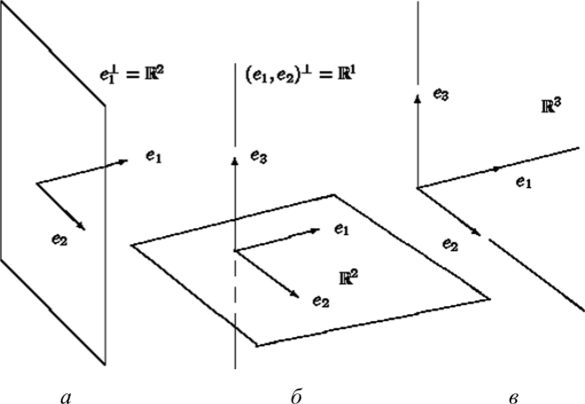
Рис. 35. Построение полной системы ортогональных векторов в R '

Полная ортонормированная последовательность векторов {.

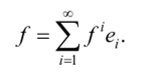
Поскольку коэффициенты /' однозначно определяются равенством /' =(/,?,), нам надо доказать, что если { T-^е— предел любой последовательности Коши элементов из Я есть элемент из Я. Иначе говоря, для любых а_х, а₂,…, а_т и любого т существует элемент / е Я, такой, что.

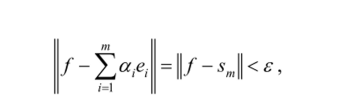
где е — любое заданное положительное число (обратите внимание, что последовательность элементов, стремящаяся к /, образована не эле;

III.

ментами a_je_j, а частичными суммами s_m = У^ог.-е,-, которые сами явля;

i=i.

ются элементами из Н). В силу же свойства наилучшего приближения ряда Фурье, имеем.

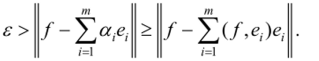
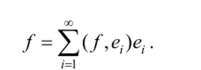
Переходя к пределу по т —> со, при произвольном ? получаем равенство Таким образом, ряд Фурье действительно сходится к элементу / е /7, и потому последовательность {е,} есть базис. Раз последовательность {е₍ } является ортонормированной, то и базис, сю образованный, называется ортонормированным. И наконец, можно показать, что сепарабельное гильбертово пространство Н имеет ортонормированный базис. Действительно, если Н сепарабельно, то оно содержит счетное плотное множество {/"}? Ортогонализусм {f_n} с помощью процесса ГрамаШмидта, отбрасывая те /_и, которые оказываются линейно зависящими от уже образованных ортонормированных векторов е_г Полученное ортонормированное множество {е, } может быть конечно, тогда и Н — конечномерно. В любом случае оно полно, гак как линейная оболочка, образованная векторами {/"}, совпадает с линейной оболочкой, образованной векторами {е_п} (в процессе ортогонализации мы отбрасывали только линейно зависимые векторы), а {/',} плотно в Н. Следовательно, вектор, ортогональный всем векторам из {е"}, есть нулевой вектор. Таким образом, ортонормированное множество {е_п} полно, а значит, образует ортонормированный базис сепарабельного гильбертова пространства Н. Существование базиса делает гильбертово пространство Н подобным (или, как говорят, изоморфным) евклидову пространству Rⁿ (если Н конечномерно) или пространству i₂ — пространству бесконечных последовательностей чисел с евклидовой нормой (если Н бесконечномерно).