Проницаемость перколяционных сред

Рассмотрим теперь течение флюида сквозь плоскую мембрану (или фильтр) с различным содержанием случайно распределённой проницаемой фазы (например, пор). Первоначально мембрана не содержала пор и проникновение в неё флюида было невозможно. При появлении пор, когда их содержание ф мало (ф<�ф_с), флюид проникает в материал по открытой пористости (рис. 8) на входной стороне мембраны, открытая пористость на выходной поверхности никакой роли в фильтрации не играет. Замкнутая пористость выполняет роль ловушек, удерживающих флюид. По мере развития пористости число открытых пор увеличивается и флюид начинает более активно поглощаться мембраной, его количество в ней увеличивается. Постепенно течение по открытой пористости развивается, продвигаясь с обеих сторон пластины в глубь мембраны. При ф=ф_с наступает порог перколяции — начинается сквозное течение флюида через мембрану. При дальнейшем увеличении ф (ф>ф_с) число сквозных путей возрастает, открытая и замкнутая пористости постепенно исчезают и проницаемость увеличивается по параболическому закону, стремясь к постоянному значению.

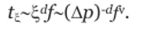aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Рис. 8. Эволюция перколяционной среды (фильтр или мембрана): а — до порога перколяции, б — на пороге перколяции, в — после порога перколяции.

Во фрактальном режиме время, за которое диффузионный фронт переместится на расстояние R, равно t~R^df, в частности, расстояние, равное длине корреляции,% будет преодолено за время.

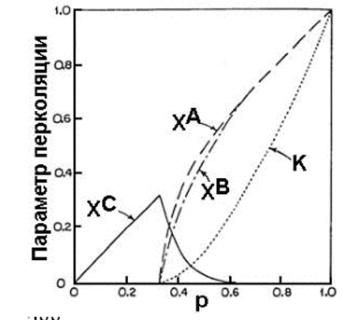
Рис. 9. Типичные зависимости некоторых перколяционных параметров в пористой среде от доли открытых пор: X⁴- доступная для диффузии доля открытых в сквозном кластере; Л*- доля открытых пор в скелете; X^е- изолированная доля открытых пор; Кобщая проницаемость системы; Х^в<�Х⁴ Х^С=Х^А-Х^В.

На больших масштабах поведение системы становится однородным. При этом t/ti=R/?. Таким образом, за время t"t_? фронт возмущения распространится на расстояние R^/tc)t; эффективная скорость его распространения u~?/f_?~(Ap)(^dr^l)v. Показатель ip=(d/-i)v эффективной скорости определяет величину критического замедления. При размерности d=2 Ф=о, 13, а при d=з vp=o, 3i. В классической области ip=o, 5.

В случае приближения к порогу перколяции сверху (для ф>ф_с) константа проницаемости: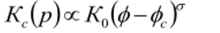

*__*__*.

Теория протекания, в своё время введённая в противовес диффузионному механизму, в конечном счёте способствовала развитию общей теории диффузии. Особенно ценными оказались понятия порога перколяции, размерного спектра кластеров, бесконечного кластера, его скелета и самоподобия, фрактальности у порога перколяции, флуктуации плотности и т. п. Важно также, что перколяция рассматривает фазовые образования неопределённой структуры и попутно позволяет оценить адекватность формул для эффективного коэффициента диффузии в дисперсиях простой геометрической формы. Обнаружение степенных законов и связикритических индексов с показателями фракталов поставили теорию фильтрации на твёрдую математическую основу. В то же время теория перколяции имеет ограниченное применение в диффузии, поскольку' рассматривает только дву^хкомпонентные контрастные структуры и только стационарное течение.