Уравнения кинетики реакций

Если выражение закона действующих масс для данной реакции известно, то функциональная зависимость молярной концентрации участвующих в реакции веществ от времени c (t) может быть получена в аналитическом виде. Соответствующая функциональная зависимость называется уравнением кинетики рассматриваемой реакции.

Наиболее простой вид имеет уравнение кинетики реакции первого порядка. Например, экспериментальное изучение реакции гидролиза сахарозы с водородхлоридом в водном растворе позволяет представить полученные данные следующим образом:

где с_с — молярная концентрация сахарозы, моль/л; к — константа скорости реакции первого порядка.

Выражение (6.3) представляет собой линейное дифференциальное уравнение первого порядка. Его интегрирование дает уравнение кинетики реакции первого порядка.

где с_с0 — начальная концентрация сахарозы.

Таким образом, в данном случае зависимость концентрации реагента от времени описывается показательной (экспоненциальной) функцией. Очевидно, что график этой функции представляет собой теоретическую кинетическую кривую реакции первого порядка. Теоретическая зависимость (6.4) позволяет заранее рассчитать концентрацию реагента в любой интересующий исследователя момент времени, если известны константа к и начальная концентрация Со. Следовательно, существует возможность прогнозировать протекание реакции во времени.

Экспериментальные кинетические кривые также позволяют предсказывать протекание реакции, но лишь для изученных начальных концентраций и интервалов времени. В этом заключается одно из преимуществ теоретического описания. Кроме того, с помощью уравнения (6.4) можно отыскать удобный способ обработки экспериментальных данных в целях определения суммарного порядка реакции и константы скорости.

Логарифмируя выражение (6.4), получаем.

после перехода к десятичным логарифмам ;

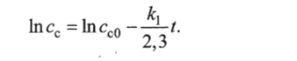
Из выражения (6.5) следует, что зависимость логарифма концентрации реагента lgс от времени / (полулогарифмические координаты) для реакции первого порядка представляет собой прямую линию. Тангенс угла наклона прямой равен к12,Ъ, откуда нетрудно рассчитать значение константы к. По аналогичной схеме находят уравнение кинетики реакции произвольного порядка.

Например, из экспериментальных данных по изучению СОЭ (см. далее) ясно, что агглютинация эритроцитов описывается уравнением кинетики второго порядка.

где с, — концентрация эритроцитов в плазме, л, к₂ — константа скорости реакции второго порядка.

Выражение (6.5) — это линейное дифференциальное уравнение первого порядка второй степени по концентрации с* Его интегрирование дает уравнение кинетики реакции второго порядка.

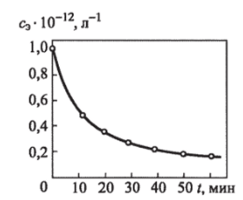
Рис. 6.4. Зависимость концентрации эритроцитов от времени.

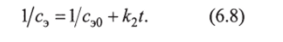
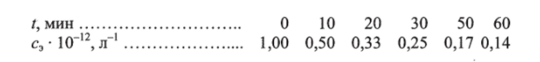
где Сэо — начальная концентрация эритроцитов.

Таким образом, зависимость концентрации эритроцитов в плазме от времени описывается рациональной дробной функцией (уравнение гиперболы). Очевидно, что график этой функции представляет собой теоретическую кинетическую кривую реакции второго порядка.

На основе теоретического уравнения кинетики (6.7) получают удобный способ графической обработки экспериментальных данных для реакций второго порядка. Для этого уравнение (6.7) преобразуют к виду Из выражения (6.8) следует, что зависимость обратной концентрации реагента 1 /с_э от времени t для реакции второго порядка — прямая линия.

Для примера приведем значения концентрации эритроцитов в зависимости от времени (рис. 6.4):

Экспериментальные точки находятся на одной прямой, что согласуется с законом второго порядка для СОЭ. Тангенс угла наклона прямой &2 = КГ¹³ л/мин.

Реакция агглютинации эритроцитов представляет собой частный случай уравнения кинетики второго порядка (уравнение (6.6)), когда начальные концентрации реагентов равны. В общем случае, согласно закону действующих масс, для скорости (6.2) дифференциальное уравнение, описывающее реакцию второго порядка, имеет вид.

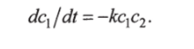
Рассмотрим следующую реакцию:

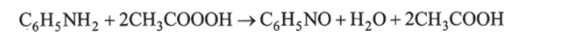
Убыль реагентов от некоторого начального значения.

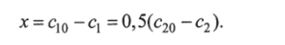
Используя метод разделения переменных, можно получить аналитическое решение уравнения кинетики:

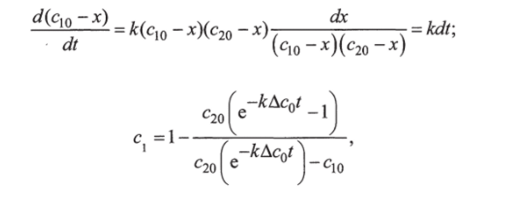
где Ас₀ =с₂₀ — с₁₀.

Важная количественная характеристика протекания реакций во времени — время полупревращения /щ реагента. Эта величина определяется промежутком времени, в течение которого начальное количество щ или начальная концентрация со реагента уменьшаются в ходе реакции в 2 раза, т. е. наполовину.

Если уравнение кинетики реакции известно, то время полупревращения нетрудно выразить через константу скорости, для чего в уравнение кинетики подставляют значения t = t_m и с = = с₀/2. В результате из уравнения кинетики реакции первого порядка (6.4) имеем.

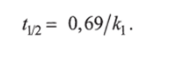
Из уравнения кинетики реакции второго порядка (6.6) соответственно получают

Как правило, в метаболических превращениях участвует несколько реагентов: субстраты, ферменты, коферменты, кофакторы. Часто не все участвующие в реакции вещества известны, поэтому за ходом превращения следят по изменению количества или концентрации одного, реже двух реагентов или продуктов. В таких случаях выразить скорость через концентрацию невозможно и время полупревращения используют как удобную кинетическую характеристику изучаемого вещества. При этом необходимо иметь в виду, что в отличие от константы скорости кинетическая характеристика может зависеть от начальной концентрации вещества. Данный факт наглядно демонстрируется выражением для времени полупревращения реакции второго порядка (6.9): время ty2 зависит не только от константы скорости, но и от концентрации реагента.