Диффузионный процесс, или процесс Ито. 
Интеграл Ито, формула Ито

Представленный в предыдущем подпараграфе винеровский случайный процесс в силу своих свойств часто выступает в роли базового в конструкции так называемых диффузионных процессов X_t, t> 0, являющихся решениями стохастических дифференциальных уравнений вида.

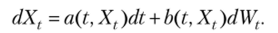
Последнее уравнение является компактной записью соотношения.

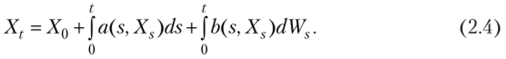
Второй интеграл, входящий в выражение (2.4), понимается как стохастический интеграл Ито по винеровскому процессу. Другими словами, интегралом Ито называется интеграл случайной функции b (t, X,) по винеровскому процессу, имеющий следующий вид:

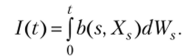
В классическом математическом анализе рассматриваются различные подходы к понятию интегрирования функций, которые приводят к отличающимся видам интегралов, таким как, например, интегралы Ньютона, Римана, Лебега и др. В теории стохастических процессов также рассматриваются разные подходы к интегрированию случайных функций по случайным процессам, приводящие к различным видам стохастических интегралов.

Одним из первых проблему интегрирования по случайным процессам рассмотрел Н. Винер. В своих работах^[1] он дал определение стохастического интеграла для детерминированных, т. е. неслучайных, гладких функций. В данном случае стохастический интеграл l (t) определяется следующим соотношением:

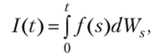
где f (s), s > 0, — детерминированная функция времени.

Поскольку функция f (s) является дифференцируемой, можно воспользоваться методом интегрирования по частям. В результате получим.

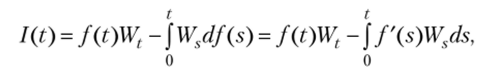
t.

где интеграл ff'(s)W_sds понимается как потраекторный, т. е. для каждой о реализации случайной величины со как интеграл Римана от непрерывной функции f'(s)W_s(со), s > 0.

В 1944 г. японский математик К. Иго (Ito) сделал существенный шаг в теории стохастического интегрирования, обобщив результат Винера на случай не только детерминированных, но и случайных функций. Таким образом, К. Ито сделал существенный шаг в расширении понятия стохастического интеграла, что, в свою очередь, привело к развитию стохастического исчисления, являющегося наиболее мощным на сегодняшний день инструментом исследования и анализа случайных процессов. Соответственно, предложенный Иго интеграл случайной функции по винеров;

t

скому процессу I (t) = jf (s, co) dW_s носит его имя.

о Перейдем непосредственно к определению интеграла Ито. Разобьем отрезок [0; t] на п частей следующим образом: 0 = ?₀ < t_x <… < t_n = t и введем в рассмотрение сумму.

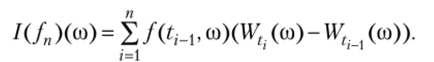
В простейшем случае потребуем, чтобы /(s, со) была адаптирована к винеровскому процессу, т. е. была функцией (W_x, 0 < х < s) и, таким образом, зависела только от его текущего и прошлых значений. Кроме того, будем предполагать выполнение условия.

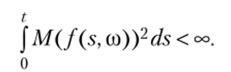
В этой ситуации можно показать, что существует единственная случайная величина /(/)(со), такая что имеет место сходимость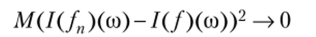

при п —> и условии равномерного дробления отрезка [0; t. Тогда под интегралом Ито понимается указанная случайная величина и, таким образом,.

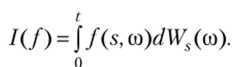
Интеграл Ито обладает следующими свойствами.

f^e)

• 1. Равенство нулю математического ожидания: М j f (s, (ri)dW_s((o) = 0.
• (ft у’j ft
• 2. Изометрическое свойство: M jf (Sy (o)dW_s -M J/²(s, (o)ds .

^Vo ) J U )

Представленное понятие стохастического интеграла играет ключевую роль при определении следующего класса непрерывных случайных процессов, имеющих важное значение для моделирования цен финансовых активов.

Случайный процесс X_f1 t > 0, называется процессом Ито, если существуют два процесса a (t, со) и b (t, со), для которых выполняются условия и.

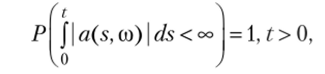
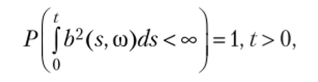
такие что.

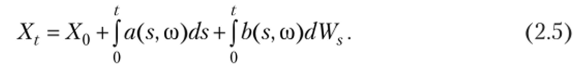
Вместо интегральной записи (2.5) часто используют дифференциальную: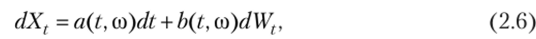

где под стохастическим дифференциалом dX_t понимается приращение X_t+(j_t — X_t процесса X_t с точностью до членов порядка dt. При этом говорят, что процесс Ито имеет стохастический дифференциал (2.6).

Если задана непрерывная функция U (t_f х), t > 0, имеющая непрерыв- dU дU d²U _v

ные производные ——, —— и —г, и Х₍ является случайным процессом Ито, at ох дх¹

то при этих предположениях случайный процесс U (t, Х_{) также является процессом Ито. При этом его стохастический дифференциал определяется соотношением.

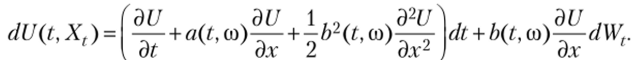
Данное соотношение называется формулой Ито. Отметим, что указанная формула может быть переписана в эквивалентной форме.

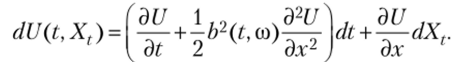
Строгое доказательство формулы Ито представлено в целом ряде источников¹. Общая схема основывается на представлении дифференциала dU (t, X,) в виде разложения в ряд Тейлора.

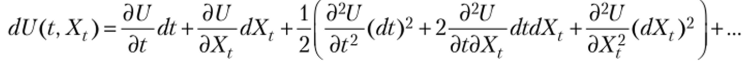
Durrett R. Brownian motions and martingales in analysis. Belmont, CA. Wadsworth, 1974; Жаков Ж., Ширяев A. II. Предельные теоремы для случайных процессов. Т. 1, 2. М.: Физматлит, 1994.

с последующим исключением членов, имеющих порядок малости более высокий, чем dt, исходя из свойства винеровского процесса (2.3).

Приведем также многомерный вариант формулы Ито. Случайный процесс X = (Х_{, Х₂, X_N), где Xj = (X_it)_t>₀, называют N-мерным процессом

Ито, если существуют вектор а = (a_t, a_N) и матрица b = || Ь_{] ||_iVxAr ^с компонентами а_г = я_;(?, со) и bjj = b;j (t,со) соответственно, удовлетворяющие условиям, аналогичным представленным выше для процессов я (?, со) и b (t> со), такие что для всех i = 1,…, N выполняются соотношения.

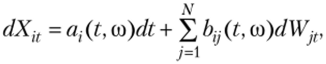
где WJy — набор независимых стандартных винеровских процессов J = 1,…, N.

Независимость двух винеровских процессов W_jt и означает выполнение равенства.

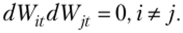
Последнее соотношение расшифровывается следующим образом:

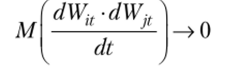
при dt-^ti j.

Для доказательства того, что из независимости винеровских процессов, означающей независимость случайных величин W_ir и W-_jt для любого фиксированного момента времени t, следуют указанные соотношения, ввс;

дем в рассмотрение случайный процесс W_t = —^(W_it+Wj_t), который, как.

v 2.

нетрудно убедиться, является также винеровским в силу независимости исходных винеровских процессов. Заметим, что выражение.

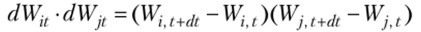
можно преобразовать, используя процесс W_t, следующим образом:

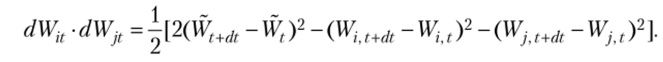
Правая часть полученного соотношения в силу формулы (2.3) стремится к нулю при dt —> 0, что и завершает доказательство отмеченного свойства. Таким образом, в данном случае, если U (t, x_]y…_yx_N) представляет собой ЭU bU d²U.. ,.

функцию с непрерывными производными ——, —— и ——-—, i, j = 1, …, N, то.

Ot OX; ox fix i

имеет место iV-мерный вариант формулы Ито:

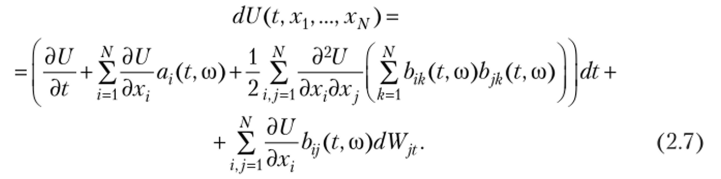
Следует отметить, что в практических приложениях часто считается, что случайные процессы Х_и имеют независимые шумы.

Важно, что указанное предположение не означает независимость самих процессов X_it В частности, формула (2.7) позволяет в ряде случаев в явном виде определять стоимость различных финансовых инструментов (например, опционов), которые, в свою очередь, зависят от стоимости некоторых базовых активов (например, акций).

Если винеровские процессы W_it и Wj_t зависимы, то имеет место соотношение.

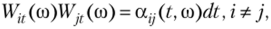
где случайная величина, а ,-,(?, со) носит название коэффициента корреляции. В этом случае нетрудно убедиться, что формула Ито приобретает следующий вид:

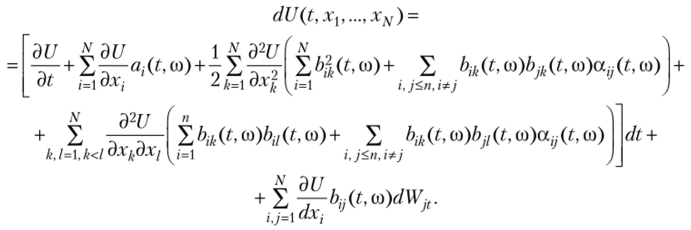
Формула Ито имеет целый спектр приложений при анализе случайных процессов вида (2.6). С одной стороны, эта формула позволяет вычислять стохастические интегралы. Рассмотрим следующий пример. Пусть W_t — стандартный винеровский процесс. Необходимо вычислить интеграл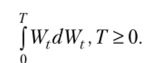

Другими словами, требуется вычислить интеграл винеровского процесса по винеровскому процессу. Рассмотрим процесс X_t, определяемый соотношением dX_t = dW_t, Х₀= 0. Очевидно, что X_t = W_L. Теперь применим формулу Ито к функции U (t, X_t) = X}. Сравнивая соотношение dX, = dV_t с выражением (2.6), отметим, что в данном конкретном случае a (t, со) = 0, а b (t, со) = 1. Кроме того,.

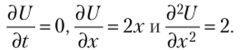
Учитывая полученные соотношения, имеем.

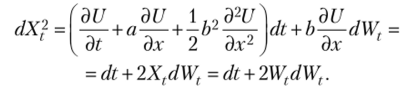
Интегрируя обе части последнего равенства, получаем 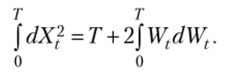Тогда, учитывая, что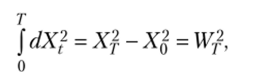

окончательно получим.

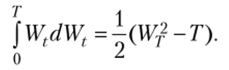
Следует отметить, что если бы функция W_t была непрерывно дифференцируемой, то указанный интеграл должен был быть равен — 1Т/, поскольку в этом случае он представлял бы обычный интеграл Римана.

С другой стороны, формула Иго предоставляет инструмент моделирования цен финансовых активов, в основе которых лежат более простые инструменты, динамика стоимости которых описывается процессом Ито. Например, в дальнейшем будет показано, что цены акций следуют процессу Ито, имеющему определенный вид функций a (t, со) и b (t> со). Тогда стоимость любого срочного контракта, основанного на данной акции, также будет следовать процессу Ито, поскольку, очевидно, стоимость указанного контракта является функцией цены базового актива.

Рассмотрим важный частный случай применения формулы Ито, связанный с выводом уравнений для математического ожидания и дисперсии случайного процесса, удовлетворяющего линейному стохастическому дифференциальному уравнению. Значение процессов указанного типа заключается в том, что таковыми являются случайные процессы стоимости портфелей, составленных из финансовых активов различного типа, например акций и облигаций. Пусть процесс X_t, значение которого в момент времени t — 0 равно заданному значению Х₀> удовлетворяет уравнению вида.

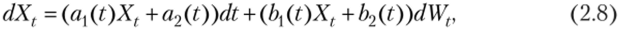
где a_x(t), a₂(t), b_{(t) и b₂(t) — детерминированные функции времени.

Требуется определить значение математического ожидания р (?) = МХ_{ и дисперсии DX_t случайного процесса X_t на момент времени t. Обозначим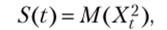

тогда

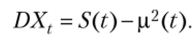
Таким образом, для решения поставленной задачи достаточно вывести уравнения для функций р (?) и S (t). Представим выражение (2.8) в интегральной форме:

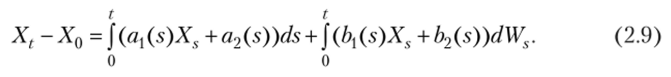
Применяя функцию математического ожидания к левой и правой частям уравнения (2.9) и учитывая, что математическое ожидание интеграла Ито равно нулю, получим.

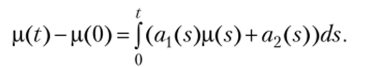
Ив последнего соотношения непосредственно можно получить обыкновенное дифференциальное уравнение для функции р (?):

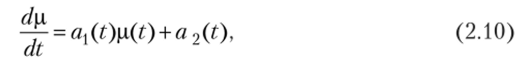
при этом р (0) = Х₀.

Для определения S (t) введем функцию U (t, х) = х². Тогда по формуле Ито.

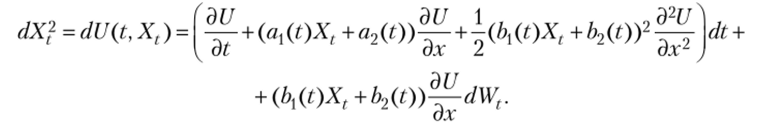
Преобразуем последнее соотношение к интегральному виду и приравняем математические ожидания его левой и правой частей. С учетом соот;

. dU dU ₀ Э4J ₀

ношении —— = 0, —— = 1х и —- = 2 получим at ох ох²

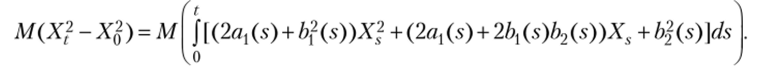
Тогда S (t) определяется как решение дифференциального уравнения.

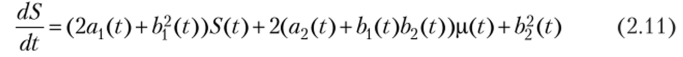
с начальным условием S (0) = Xfi.

• [1] Wiener N. Differential space // Journal of Mathematical Physics. Mass. Inst. Tech., 1923.Vol. 2. P. 131−174.