Корреляционное отношение Пирсона г

Все рассмотренные выше коэффициенты корреляции служат для выявления только линейной зависимости между признаками. Для измерения нелинейной зависимости К. Пирсон предложил показатель, который он назвал корреляционным отношением. Напомним, что коэффициент корреляции г_ху (формула 9.1), который был введен Пирсоном, характеризует связь между переменными х и у с точки зрения прямой или обратной пропорциональной зависимости. Иными словами, получаемая связь между переменными является линейной (согласованной) и такой, что с увеличением одной переменной другая (в среднем) либо только увеличивается, либо только уменьшается (в среднем). При этом в первом случае говорят о положительном коэффициенте корреляции, во втором — об отрицательном.

Корреляционное отношение описывает искомую связь, условно говоря, с двух сторон: со стороны переменной х по отношению к у и со стороны переменной у по отношению к х. Соответственно этому корреляционное отношение представляет собой два показателя, обозначаемые как h_yx и h_xy. Они вычисляются отдельно друг от друга. Однако они связаны между собой, поскольку при строго линейной зависимости между переменными х и у имеет место равенство h_yx = h_xy. В этом случае величины обоих показателей корреляционного отношения совпадают с величиной коэффициента корреляции Пирсона.

Показатели корреляционного отношения вычисляются по следующим двум формулам:

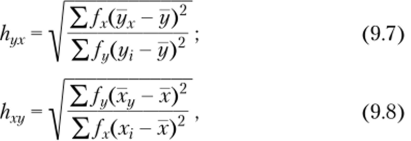
где х и у общие, а х_у и у_х — групповые средние арифметические; f_y и f_x — частоты рядов х и у.

Согласно этим формулам оба показателя всегда положительны и располагаются в интервале от 0 до +1.

Подчеркнем, что, как правило, h_yx ^ h_xy. Равенство между этими коэффициентами возможно лишь при наличии строго линейной связи между коррелируемыми переменными. Именно поэтому различие между h_xy и h_yx означает наличие не линейной, а связи более сложного типа между коррелируемыми переменными. Конструкция корреляционного отношения предполагает сопоставление двух видов изменчивости особым образом вычисленных значений х и у. Во-первых, это изменчивость отдельных вариант (значений) самих переменных х и у по отношению к так называемым частным средним величинам этих переменных. Во-вторых, это изменчивость (вариация) этих частных средних по отношению к средним величинам этих переменных. При этом если величины переменных х и у не варьируют вокруг соответствующих частных средних, то полученная в данном случае теснота связи будет большой. И, напротив, если изменчивости частных средних вокруг соответствующих средних величин не наблюдается, то связь отсутствует. В целом же, чем меньшую часть составит первая величина по отношению ко второй, тем больше теснота нелинейной зависимости между признаками.

Для вычисления корреляционного соотношения h_yx (г/ но х) или h_xy (х но у) необходимо выполнить следующие действия:

• 1) расположить, но порядку исходные данные по х от меньшей величины к большей, при этом сохранив значения соответствующих величин у. Требование сохранения соответствующих величин у означает следующее: предположим, что испытуемый А получил по х значение, равное 10, а по у — значение, равное 4, — эта связка (х = 10 и у = 4) должна сохраняться всегда во всех преобразованиях, поскольку именно эти значения получил в эксперименте испытуемый Л;
• 2) определить частоты переменной х — обозначение f_x и расположить их в строчку;
• 3) определить величины х, — как все значения переменной х_у но без повторов, для соответствующей частоты f_x. Проще говоря, все значения переменной х переписываются без повторов. Полученные величины Xj следует расположить в строчку под соответствующими частотами f_x;
• 4) подсчитать арифметические (частные) средние, но переменной У для соответствующей частоты f_x — обозначение

у_х и расположить их в строчку под значениями Xj (процедура расчета будет понятна из примера);

• 5) расположить по порядку исходные данные по у от меньшей величины к большей, при этом сохранив значения соответствующих величин х;
• 6) определить частоты переменной у — обозначение f_y и расположить их в строчку;
• 7) определить величины у, как все значения переменной у, но без повторов для соответствующей частоты f_y. Иными словами, все значения переменной у переписываются без повторов. Полученные величины у-, следует расположить в строчку под соответствующими частотами /_у
• 8) подсчитать арифметические (частные) средние по переменной х для соответствующей частоты f_y — обозначение х_у и расположить их в строчку под значениями г/, (процедура расчета будет понятна из примера);
• 9) определить общие средние, но переменной х и у (обозначение х и у);
• 10) произвести расчет по формулам (9.7) и (9.8);
• 11) определить уровень значимости полученных показателей корреляционного отношения по таблице критических значений для критерия t Стыодента при k = п — 2.

На конкретном примере рассмотрим, как производить расчет показателей корреляционного отношения.

Задача 9.3. Психолог у 8 подростков сравнивает баллы по третьему, математическому субтесту теста Векслера (переменная х) с оценками по алгебре (переменная у). Интересующие психолога вопросы можно сформулировать двояко. Первый вопрос — связана ли успешность решения третьего субтеста Векслера с оценками по алгебре? И второй — связаны ли оценки по алгебре с успешностью решения третьего субтеста Векслера?

Решение. Представим полученные экспериментальные данные в следующем виде:

Напомним, что пара величин [8, 21 была получена для испытуемого Л, величины [18, 3] — для испытуемого В, величины [18, 4] для испытуемого С и т. д. Иными словами, полученные соотношения (связки) между значениями величин х и у в процессе вычислений произвольно менять местами нельзя.

Подчеркнем также, что если мы рассчитаем коэффициент линейной корреляции Пирсона, но формуле (9.1), то получим величину г_ху = 0,244. Этот коэффициент незначим, и, следовательно, линейной связи между переменными х и у нет. Нам же в этой задаче нужно выяснить — существует ли между двумя вышеприведенными переменными другой тип связи, а именно нелинейная связь.

Произведем расчет согласно п. 1 — 11.

1. Расставим по порядку величины х от меньшей к наибольшей, сохраняя соответствие с исходными данными по у

2. Определяем частоты переменной х (обозначаемые f_x). Частоты вычисляются по правилу, изложенному в параграфе 3.2. Согласно этому правилу, если какое-либо значение встречается в анализируемом ряду один, два, три и большее число раз, то этому значению проставляется частота, равная соответственно числу один, два, три и большим числам. Так, в нашем случае значение 8 встречается два раза, следовательно, его частота равна 2, значение 10 также два раза, следовательно, его частота также равна 2 и т. д. Получим следующее:

Проверим правильность подсчета частот — их сумма должна равняться числу варьирующих значений переменной х.

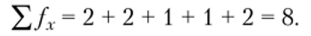
3. Находим неповторяющиеся значения переменной .г (обозначающиеся как Xj):

4. Подсчитываем арифметические частные средние для переменной у по отношению к переменной х. Для этого одним и тем же значениям вставим в соответствие их среднее арифметическое по у следующим образом: в исходных данных двум значениям 8 и 8 нох соответствовали величины 2 и 3 по у, следовательно, одному значению х (равному 8) будет соответствовать частное среднее по г/, равное (2 + 3)/2 = 2,5. Значению 10 но л: соответствует (4 + 5)/2 = = 4,5. Соответствие между числами 14 и 5 и 16 и 4 остается неизменным. Значению 18 под: будет соответствовать частное среднее, равное (3 + 4)/2 = 3,5. Таким образом, построено новое распределение из частных средних значений переменных у по отношению к значениям х. Расположим полученные величины следующим образом:

5. Расставим по порядку величины у от меньшей к наибольшей, сохраняя соответствие с исходными данными пог.

6. Подсчитаем соответствующие частоты:

Проверка правильности подсчета частот: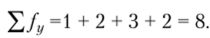

7. Неповторяющиеся значения у.

8. Подсчитаем соответствующие частные средние иод: 8/1 = 8, (8 + 18)/2 = 13, (10 + 16 + 18)/3 = 14,7 и (10 + 14)/2 = 12. Расположим полученные величины следующим образом:

9. Теперь подсчитаем общие средние.

х- (8+ 18+ 18+ 10+ 16+ 10 + 8+ 14)/8- 102/8= 12,75- общее среднее под.

г/ = (2 + 3 + 4 + 5 + 5 + 4 + 3 + 4)/8 = 30/8 = 3,75 — общее среднее, но у.

10. Все готово для расчета по формулам (9.7) и (9.8).

246 Глава 9. Корреляционный анализ. Понятие корреляционной связи.

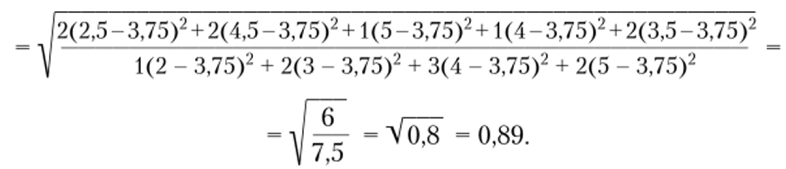
Подсчитаем теперь.

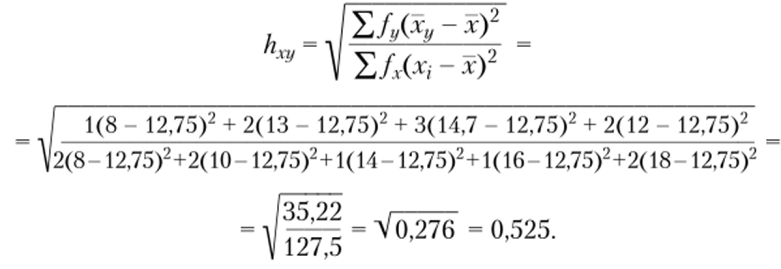
В результате получено два не равных показателя корреляционного отношения. Для проверки их значимости следует применить формулу (9.5) для k = п — 2.

Проверим на уровень значимости первый показатель.

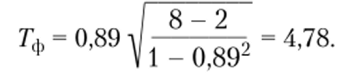
По табл. 9 Приложения для k = п — 2 = 8- 2 = 6 находим: 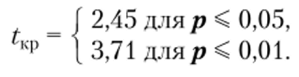Строим соответствующую «ось значимости»:

Можно сделать вывод о том, что полученный показатель значим. Принимается гипотеза Н.

Подсчитываем уровень значимости второго показателя:

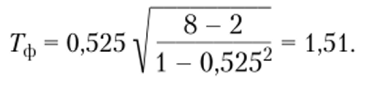
Поскольку критические значения уже найдены выше, сразу строим соответствующую «ось значимости»:

Следовательно, полученный показатель незначим. Принимается гипотеза 7/₀.

Таким образом, можно сделать вывод о том, что в данном случае есть значимая положительная связь между у и х, а обратной связи между х и у нет. Следовательно, решение искомой задачи может звучать так: хорошее знание алгебры положительно связано с эффективностью работы с третьим субтсстом Векслера, и, напротив, успешное решение третьего субтеста Векслера никак не связано со знанием учащимися алгебры. Иными словами, чем лучше учащиеся знают алгебру, тем лучше их показатели по третьему субтесту Векслера. И напротив, высокая успешность решения третьего субтеста Векслера не влечет за собой хорошее знание учащимися алгебры. Подчеркнем, что полученные соотношения были получены для очень маленькой выборки — всего 8 человек испытуемых. Величина выборки столь мала, что никакие выводы в данном случае делать нельзя. Поэтому все выводы, сделанные нами, следует рассматривать только как учебные.

Разумеется, корреляционное отношение Пирсона не дает возможности установить характер выявленной связи — она может быть параболической, кубической, логарифмической и др. Из результатов анализа ясно только одно: связь между переменными х и у носит нелинейный характер. Более точно характер связи можно определить либо построив график, либо с помощью метода регрессионного анализа.

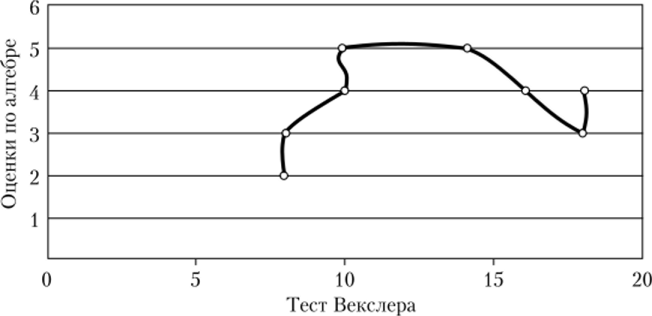
Рис. 9.10. График взаимосвязи переменных х и у.

График показывает, что переменные х и у связаны между собой зависимостью, достаточно близкой к криволинейной. Построение подобных графиков рекомендуется в каждом случае при обращении к расчетам корреляционного отношения Пирсона.

К сожалению, в психологии метод корреляционного отношения не нашел широкого распространения. Многие исследования, использующие корреляционный анализ, ограничивались нахождением только линейной зависимости между переменными, хотя нельзя исключить вероятность того, что реальные связи были нелинейными. Напомним, что в пашем примере коэффициент корреляции Пирсона, подсчитанный, но формуле (9.1), г = 0,243 оказался незначимым. Однако, как это было установлено с помощью метода корреляционного отношения, связь с одной стороны была незначимой, а с другой, напротив, высокозначимой. При этом содержательный аспект этих связей оказался гораздо богаче, чем в случае простого линейного коэффициента корреляции.

Следует особо подчеркнуть, что корреляционные отношения Пирсона являются универсальными показателями корреляционных связей, поскольку они позволяют выявить наличие связей различного типа, как линейных, так и не линейных.

Расчет корреляционного отношения Пирсона не предусмотрен в анализируемых пакетах.

Для применения корреляционного отношения Пирсона необходимо соблюдать следующие условия.

• 1. Сравниваемые переменные должны быть измерены в шкале интервалов или отношений.
• 2. Предполагается, что обе переменные имеют нормальный закон распределения.
• 3. Число варьирующих признаков в сравниваемых переменных х и у должно быть одинаковым.
• 4. Для оценки уровня достоверности корреляционного отношения Пирсона следует пользоваться формулой (9.5) и таблицей критических значений для критерия t Стьюдента при k = п — 2.