Определение сенсорного оператора: метод изоконтрастных кривых

Существует несколько психофизических процедур по определению сенсорного оператора; одним из распространенных методов является метод изоконтрастных кривых. Процедура этого метода ничем не отличается от классической процедуры определения точки субъективного равенства с помощью классических психофизических методов, например, метода подравнивания.

Метод изоконтрастных кривых основывается на положении, что сенсорный оператор устанавливает правило, как зрительная система изменяет распределение яркости объекта, т. е. его контраст. В силу этого испытуемому предъявляются эталонная синус-решетка с фиксированной пространственной частотой и контрастом и тестовая решетка, отличающаяся от эталонной и частотой, и контрастом. Задача испытуемого — уравнять тестовую решетку и эталонную по контрасту.

В результате этого метода экспериментатор получает изоконтрастную кривую, которая представляет собой зависимость физического контраста, воспринимаемого как равный эталону, от пространственной частоты. Частным случаем изоконтрастной кривой является зависимость порога контрастной чувствительности от пространственной частоты синус-решетки, которая называется функцией контрастной чувствительности наблюдателя'. Эта функция будет самой нижней кривой в диапазоне кривых зависимости физических контрастов от пространственной частоты решетки. Функция контрастной чувствительности показывает, что наша чувствительность к контрасту объекта зависит от пространственной частоты решетки (рис. 3.24). На рис. 3.24 изображены две квадратурно-волновые решетки a w б, имеющие объективно одинаковый контраст, но разную пространственную частоту. Однако субъективное восприятие контраста разнится: решетка а воспринимается менее контрастной, чем решетка б. В общем виде функция контрастной чувствительности изображена на рис. 3.25, и она представляет собой зависимость субъективного ощущения контраста от пространственного распределения яркости синус-решетки.

Рис. 3.24. Восприятие контраста решеток, отличающихся, но пространственной частоте ^1[1]

В результате метода изоконтрастных кривых экспериментатор получает кривую, с помощью которой в итоге ряда математических преобразований можно построить функцию контрастной чувствительности испытуемого, отражающей зависимость контраста от пространственной частоты. Эта функция и является искомым оператором, так как позволяет проследить, как пространственно-временные характеристики яркости стимула (физический контраст при данной пространственной частоте) отображаются в субъективное ощущение светлоты в сознании наблюдателя.^[2] Таким образом, зная реальное распределение яркости и зная, что зрительная система раскладывает распределение яркости в ряд Фурье, можно через функцию контрастной чувствительности узнать, как это распределение будет отображаться в сознании у наблюдателя в субъективное ощущение светлоты.

Рис. 3.25. Функция контрастной чувствительности.

В качестве примера использования сенсорного оператора рассмотрим отображение в сознании зрительного образа решетки, изображенной на рис. 3.26, а. Это будет квадратурно-волновая решетка, так как зрительный паттерн представляет собой чередование черных и серых полос постоянной яркости. Распределение яркости этой решетки на сетчатке глаза представлено на рис. 3.26, б. Для того чтобы узнать, как наблюдатель будет субъективно воспринимать распределение яркости этой решетки, необходима функция контрастной чувствительности K (J)¹ для данного диапазона.

яркости и частоты, которую можно получить при помощи метода изоконтрастных кривых. Такая функция представлена на рис. 3.26, в.

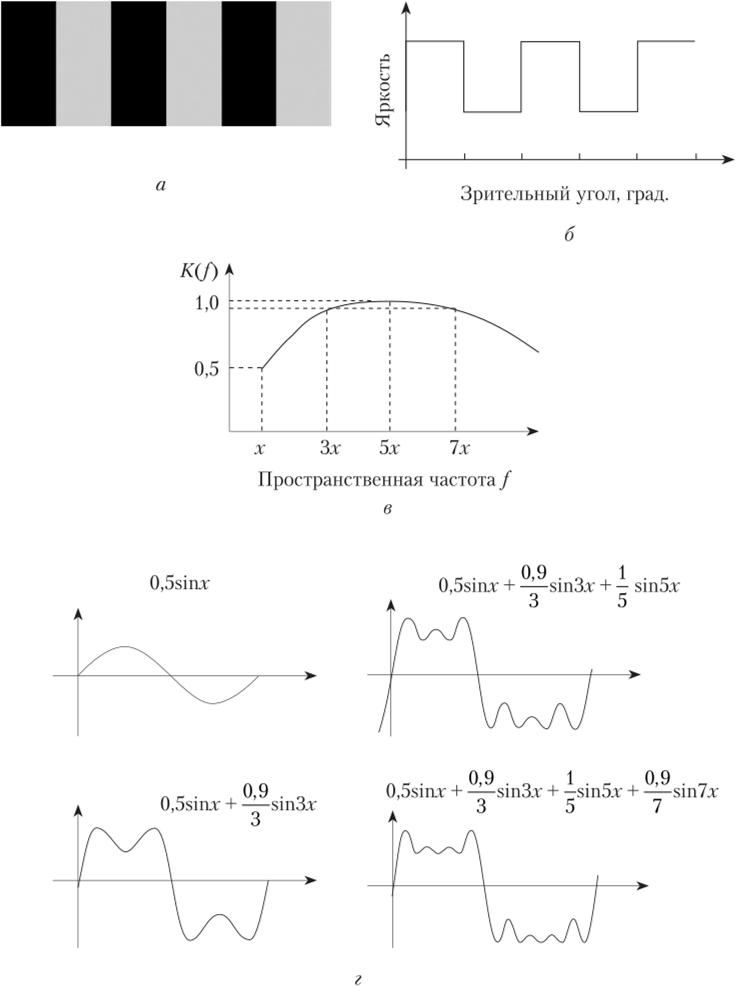
Глядя на эту функцию, можно сказать, что наблюдатель чувствителен к контрасту при частоте х в два раза меньше (значение контрастной чувствительности равно 0,5), чем к контрасту при частоте 5х (значение контрастной чувствительности равно 1). Разложение распределения светлоты в ряд Фурье дает следующую формулу:

Данная формула представляет собой ряд простых синусоидных функций со своим передаточным коэффициентом. Расчет передаточных коэффициентов осуществляется, но графику кривой контрастной чувствительности.

Исходя из формулы (3.19) и графика на рис. 3.26, 6, первый элемент ряда (т.е. для п = 1) siar будет иметь коэффициент К (х) = 0,5, второй элемент ряда (п = 2) sin3x будет иметь коэффициент К (3х) = 0,9, третий элемент ряда (п = 3) sin5x будет иметь коэффициент К (5х) = 1, четвертый элемент ряда (п = 4) sin7x будет иметь коэффициент К (7х) = 0,9 и т. д. Формула (3.19) раскладывается:

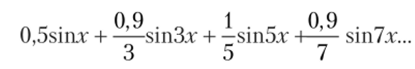
Полученные компоненты и результат их последовательной суммации показаны на рис. 3.26, г. Эти данные позволяют предположить, как испытуемый будет субъективно воспринимать это распределение. Очевидно, что светлота не будет одинаковой по всей поверхности каждой светлой и темной полосы, хотя объективно яркость в каждой полосе распределена равномерно (рис. 3.26, б). Участки светлых полос на границе с темными будут казаться светлее по сравнению с центральными участками.

Аналогично для темных полос: участки темных полос на границе со светлыми будут казаться темнее по сравнению с центральными участками. Именно такой эффект (только в значительно большей степени) достигается при восприятии яркости небольшого замкнутого объекта на фоне обширного участка фона разной интенсивности. Такой эффект называется одновременным (светлотным) контрастом, описанным выше (рис. 3.19). Частным случаем этого эффекта являются полосы Маха (рис. 3.20), описанные выше.

Определение временного субъективного распределения светлоты опирается на все описанные выше признаки, однако является значительно сложнее; сам сенсорный оператор, позволяющий дать отображение объективного распределения в субъективное, уже не описывается как график в простом декартовом пространстве. Еще более сложными, но и наиболее информативными являются попытки описать одновременно пространственное и временное распределение яркости. Фурье-анализ зрительного восприятия позволяет дать объяснение многим феноменам восприятия, например, имеющим место при восприятии движущегося объекта.

В последние десятилетия были получены данные о нейрофизиологических механизмах Фурье-анализа зрительного восприятия. На основании психофизических экспериментов с использованием синусоидальных и прямоугольных паттернов Колин Блэкмор с коллегами в 1968 г. высказал предположение, что зрительная система состоит из множества параллельных каналов-фильтров, каждый из которых чувствителен к определенным пространственным частотам, т. е. имеет свою полосу пропускания^[3]. В зрительной системе были обнаружены нейроны-детекторы, селективно чувствительные к различным пространственным частотам изображения. Поэтому когда на зрительную систему воздействует сложный паттерн пространственного распределения яркости, эти нейроны избирательно реагируют на определенные пространственные частоты, проводя Фурье-анализ воздействующего распределения. Также в нейрофизиологии описан механизм, отвечающий за субъективное ощущение светлоты и определяющий, почему, к примеру, светлота объекта на фоне разной интенсивности ощущается но-разному. Этим механизмом является механизм латерального торможения^[4].

Таким образом, для нормального зрительного восприятия окружающего мира необходимы пространственно-частотные каналы контрастной чувствительности, которые обеспечивают фильтрацию разных частот: высокие частоты информируют о мелких деталях объекта, средние частоты сигнализируют о контрасте и дают информацию о контурах предметов, а без низких частот было бы невозможно целостное восприятие объекта. Изучение нейрофизиологических механизмов зрительного восприятия способствовало активному развитию смежных областей науки, в частности, дало толчок к развитию теорий машинного зрения, искусственного интеллекта (см., к примеру, информационную теорию Д. Марра).

• [1] В физике функцию зависимости амплитуды синусоиды от частоты называют амплитудно-частотной характеристикой (АЧХ). В нашем случае амплитудой является контраст —разность между максимальной и минимальной яркостью.
• [2] 2 В основе такого описания оператора лежит ряд допущений, описанных подробнее в: Логвиненко А. ДДубровский В. Е. и др. Фурье-анализ зрительного восприятия.
• [3] Blakemore С., Campbell F. W. On the existence of neurones in the human visual systemselectively sensitive to the orientation and size of retinal images // Journal of Physiologv. 1969.Vol. 203 (1). P. 237−260.
• [4] См.: Шиффман X. P. Ощущение и восприятие.